摘 要: EMI的定位测试是电磁兼容测试的一个重要内容。传统的干扰源定位测试方法相对大型的电子设备而言效率和准确度都有限。本文提出一种基于空间谱估计技术的EMI定位方法,该方法使用二维空间平滑算法对电磁干扰信号进行DOA(波达方向)估计从而精确定位电磁干扰源。在MATLAB平台上编写了相关程序进行了模拟实验,实验结果证明,该方法不仅可以区分不同频率的干扰而且可以定位同频的干扰,可以为实际应用提供参考。
关键词: EMI;干扰源定位;二维空间平滑;DOA(波达方向)
0 引言
在电磁兼容现场测量中,对电磁干扰源进行快速定位可以帮助工程师快速地排除电磁干扰问题。传统的关于辐射源定位方法是使用辐射信号的频率这一信息,根据所找到的超标点频率去寻找频率相同的辐射源,但是在一个大型的电子设备或者系统中往往可能有多个位置产生相似频率的干扰,因此使用这种方法定位干扰源可能会出现误差[1]。
在基于自适应干扰抵消系统的虚拟暗室中使用信号的相关性定位电磁辐射干扰源。其使用两个探头,一个放在EUT(受试设备)附近的远场天线或者电流卡钳,一个作为近场探头[2]。用两个探头同时接收EUT辐射出的信号,通过双通道的同步接收机对接收到的两个信号进行处理,并通过研究两个信号的相关性实现干扰源的识别定位。但是基于信号相关性的定位方法需要不断地移动接收天线,而且在不同地点接收到的同一辐射信号也有变化,这都会影响定位的准确性。本文提出一种基于空间谱估计技术的电磁干扰定位方法,该方法使用二维空间平滑对电磁信号进行DOA(波达方向)估计以精确定位电磁干扰源[3]。二维空间平滑算法可以分辨出不同来向的相干信号,且具有很高的定位精度,适合用于EMC现场测量的电磁干扰源定位。
1 基本原理
1.1 MUSIC算法
假设EMC现场测量空间中入射到M元阵列的EUT辐射信号和干扰信号共计p个[4],则阵列接收信号的协方差矩阵为:

由于假设的干扰信号及EUT辐射信号与噪声是不相关的加性高斯白噪声,因此在式(1)中的第一项是满秩矩阵,s是对角阵,包含了干扰信号和EUT辐射信号的特征值。?滓2和Un是协方差矩阵对应的特征值和特征向量。故:

由于U=[Us,Un]是酉矩阵,其不同特征值对应特征向量之间正交。因此:
UsHUn=0(8)
由式(6)和式(8)知,阵列输出的方向矩阵A与协方差矩阵的干扰信号和EUT辐射信号特征向量组成的子空间矩阵Us相同。表示为:

噪声特征值对应的特征向量与信源的方向正交。得到空间谱估计形式为:
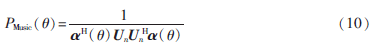
对PMusic(θ)谱峰θ域寻优,所求的θ即为入射信号的DOA的估计。
1.2 二维空间平滑算法
MUSIC不能对空间中相关的信号进行估计,且只能对信号进行一维的定位[5]。本文使用二维空间平滑算法对电磁干扰信号进行定位[6]。如图1所示的M×N的均匀矩形阵列,分成若干个重叠大小为m×n的均匀矩形子阵列。
假设K个远场窄带信源s(t)照射到这个矩形阵列上,信号的俯仰角用阵列的第(m,n)个阵元的输出为:

式中:


将图1所示的M×N的均匀矩形阵列分成若干个M0×N0的均匀矩形子阵,如图2所示。

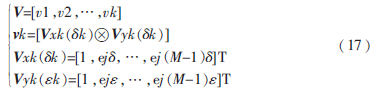
第(m,n)个子阵的接收信号向量为:
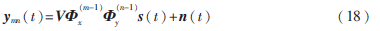
![IKP04ITMXU[D_6JKDT]9HCH.jpg IKP04ITMXU[D_6JKDT]9HCH.jpg](http://files.chinaaet.com/images/2016/02/01/6358994610779700002197761.jpg)
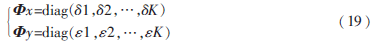
第(m,n)个子阵的协方差矩阵为:
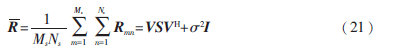
定义所有子阵的协方差矩阵的平均值为二维空间平滑协方差矩阵:
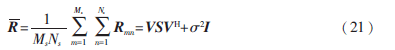
上式中Ms=M-M0+1,Ns=N-N0+1
按照MUSIC的方法对得到的协方差矩阵进行处理,估计出空间电磁干扰信号的来向。
2 实验仿真
设接收阵列为6×6的二维等距平面矩形阵列,在x轴方向和y轴方向上,阵元之间的距离均为d=400 mm。设空间中有三个不同体制下的信号,其中一个为EUT的单频辐射信号,另外两个均是电磁兼容现场测量现场的环境干扰信号或者是受试系统的其他部分发出的超标干扰源。所使用的均为窄带信号,其数学形式为:
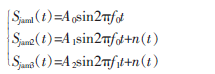
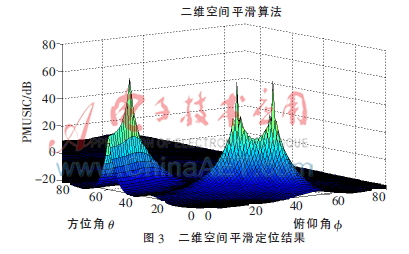
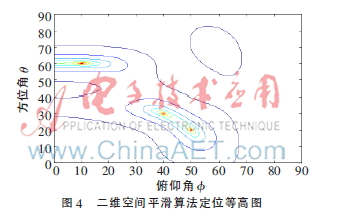
其中,A0=2A1=A2,f0=200 MHz,f1=10 MHz。n(t)是空间中的白噪声和各个阵元上的加性噪声,信噪比为20 dB。其中电磁信号的水平方位角和俯仰角为[30,40],[20,50],[60,10]。使用MATLAB软件平台对二维空间平滑算法性能进行仿真实验,取子阵为4×4的均匀矩形阵,在快拍数为500的情况下运用改进的空间平滑技术对空间中同频信号和不相关信号的估计结果如图3和图4所示。
3 结束语
实验仿真表明,通过二维空间平滑算法可以精确估计出空间中电磁信号的DOA,利用电磁干扰信号的DOA可以对大型系统或者电子设备的干扰源进行定位。较传统的频率定位法和相关性定位方法,该测试方法不仅定位方便而且可以对相干信号进行定位,因此可以应用于大型系统或电子设备的EMI测试中。
参考文献
[1] 容向系统科技有限公司.CASSPER系统技术文档[Z].2005.
[2] SCHMIDT R.Multiple emitter location and signal parameter estimation [J]. IEEE Trans on AP,1986,34(3):276-280.
[3] SHAN T J, WAX M, KAILATH T. On spatial smoothingfor direction-of-arrival estimation of coherent signals[J]. IEEE Trans on ASSP, 1985,33(4):806-811.
[4] 刘梦南.预测试中的噪声抑制与消除技术[J].安全与电磁兼容,2003(6):34-41.
[5] 程君佳,田书林,李力.电磁干扰源的相关性定位测试方法研究[J].中国测试技术,2007,33(2):42-44.
[6] 魏小丽,陈建,林琳.基于空间平滑算法的二维相干源DOA估计[J].吉林大学学报,2008,38(5):1160-1164.

