0 引言

    随着信息战技术的发展，欺骗干扰逐渐成为卫星导航系统的重要威胁。卫星导航接收机的欺骗干扰是干扰发射机发射与真实信号相类似的干扰信号，误导卫星导航接收机偏离准确的导航和定位。因而，准确识别欺骗干扰信号是卫星导航系统面临的重大挑战。从接收信号中提取出由干扰机或卫星导航发射机唯一确定的射频指纹特征是实现欺骗干扰识别的关键。

    国内外学者已提出了多种特征提取的方法，主要有时频分析^[1]、分形理论^[2]、高阶谱分析^[3-4]等，其中，高阶谱因具有时移不变性、尺度变化性和相位保持特性得到广泛应用^[3]。Wigner双谱(WB)是Gerr^[5]在1988年提出的概念，随后由Nikias^[6]推广到普遍意义上的Wigner高阶矩谱(Wigner Higher Order Moment Spectrum，WHOS)。Wigner高阶矩谱是高阶谱与Wigner时频分布结合得到的，同时具备了高阶累积量和时频分布的优良性能，得到广泛应用。然而，尚未见有基于Wigner高阶矩谱的特征提取方法的文献报道。本文对信号进行Wigner双谱分析，提取其主对角切片谱，进而提取谱熵及谱奇异值熵等特征组成特征向量，并与基于双谱的特征提取方法进行比较。实验结果表明，该方法性能有明显的优势。

1 Wigner高阶矩谱

    对任一零均值信号x(t)，信号的双谱是三阶累积量的二维傅里叶变换^[4]，定义为：

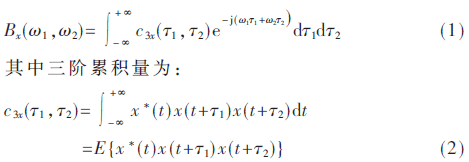
    式(1)表明频率变量w₁与w₂是等价的，因而双谱具有对称性。另外，由于高斯信号的三阶累积量为零，双谱可以有效抑制高斯噪声，因而得到广泛应用。

    WHOS是Wigner-Ville分布与高阶谱的结合。对于给定信号x(t)，其k阶WHOS由k维局部自相关函数R_kt(τ₁，τ₂，…，τ_k)的k阶傅里叶变换得到^[6]，即：

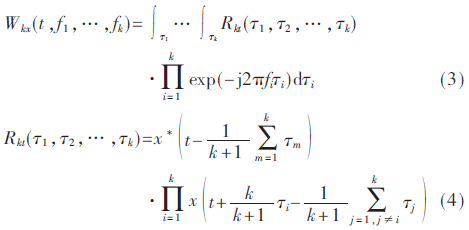
    令k=2即可得到Wigner双谱(WB)。

    同WVD等其他二次型时频分布类似的是Wigner双谱也存在着交叉项干扰的问题，这就影响了其对信号分析的有效性，因此有必要抑制其交叉项的干扰。为了消除不同的频率成分引入的交叉项的干扰，通过采用解析信号和Choi-Williams核函数^[7]来抑制交叉项干扰。该核函数的定义如下：

2 Wigner对角切片谱及二次特征提取

    WHOS可以最大化地保留信号本身的固有信息，因而非常利于提取信号的特征，但WHOS的存储量和识别的计算量都比较大。另外，WB作为三维函数，它的直接应用就要求计算复杂的三维模板匹配，因此大大限制了WB在模式识别领域的应用。

    为了克服这一困难，引入Wigner对角切片谱(Diagonal Sliced Wigner Bispectrum，DS-WB)^[8]的方法，选取WB的两个谱频率构成平面的对角切片将三维的WB变换为二维的DSWB。因为WB中两个谱频率值是对称的，对角切片上包含了WB的主要信息。根据CWB，可以定义带核函数的Wigner对角切片谱(DS-CWB)如下：

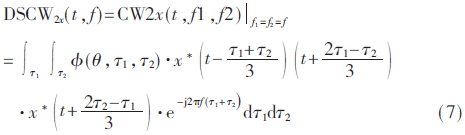
    然而DS-CWB仍为二维函数，直接使用时数据量和计算复杂度仍然很大。为了能进一步降低计算的复杂性，本文对信号的DS-CWB进行二次特征提取，提取DS-CWB谱的分布熵、奇异谱熵连同DS-CWB的均值、对数和等特征参数组成四维特征参数向量。

    对信号进行DS-CWB谱估计，可以得到一个时间-频率的二维平面。对于该平面上的每个DS-CWB谱值，设DS-CWB矩阵为S∈R^M×N，令：

    DS-CWB的分布熵用于衡量在时间-频率二维平面内能量的分布。对分布熵而言，若不同时间-频率区域能量分布均匀，则熵值最大；相反，若能量分布集中，则双谱分布熵较小。

    奇异值特征是一种性质良好的代数特征，可以作为信号的特征用于识别。为了充分利用所有奇异值信息，并且有效降低特征维度，本文利用信息熵的特性对奇异值谱进行分析，将得到的DS-CWB谱矩阵S进行奇异值分解，得到一系列奇异值组成的主奇异值向量并定义其为信号的奇异值谱。DS-CWB的奇异谱熵的表达式为：

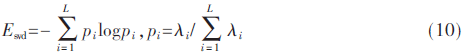
    DS-CWB的奇异值谱熵直接反映了被分析DS-CWB谱矩阵的代数特性和内在属性。对DS-CWB的奇异谱熵而言，奇异值分布越均匀，则熵值越大；反之，奇异值分布越离散，则熵值越小。

    此外，均值经常用于信号的特征提取中，用来衡量信号能量的平均程度。因此，定义二维平面内的DS-CWB分布序列的均值来表征信号的特征，即：

    还可定义DS-CWB谱的对数和作为特征，DS-CWB谱矩阵的和表示谱的能量大小，取对数可以使数据更加平稳，其表达式为：

    因此，基于DS-CWB的特征提取算法可描述如下：

    (1)对信号进行WB变换，得到三维的WB数据；

    (2)用式(7)计算DS-CWB，得到时间-频率的二维DS-CWB数据；

    (3)根据式(9)对DS-CWB矩阵提取其分布熵特征；

    (4)对二维的DS-CWB矩阵进行奇异值分解，并根据式(10)提取DS-CWB的奇异谱熵；

    (5)根据式(11)和式(12)对DS-CWB矩阵提取其均值μ、对数和H_{sum_log}；

    (6)将提取的特征组合成四维特征向量[E，E_svd，μ，H_{sum_log}]作为信号特征用于分类识别。

3 实验验证

    为了进一步验证本文所提出的基于DS-CWB的特征提取算法在欺骗干扰识别中的识别性能，采取了软件仿真与硬件实验相结合的验证方法。本文将基于DS-CWB的特征提取算法与基于双谱的特征提取算法进行比较，两种算法均分别使用奇异值特征（对信号的DS-CWB与双谱进行奇异值分解，得到奇异值向量作为识别特征）与文中所提出的四维特征作为信号的特征向量，并比较了不同信噪比的高斯噪声背景下的欺骗干扰识别效果。

3.1 软件仿真

    本文假定欺骗干扰为转发式欺骗干扰，该类干扰与真实信号有很高的相似性。设GPS信号为C/A码信号，调制方式为QPSK调制。为了仿真产生与卫星导航发射机非常相似的欺骗干扰信号，需要借助Hammerstein模型^[9]。将卫星发射机/干扰机视为一个静态非线性子系统，该子系统可以用一个无记忆多项式模型表示；并将无线信道视为一个动态线性子系统， 该子系统可以用一个FIR滤波器表示。二者级联得到输入与输出的关系为：

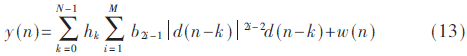
    其中，M是多项式系数个数，d(n)是输入信号，b_2i-1为多项式系数，h_k是信道响应系数，N是FIR滤波器阶数，w(n)~N(0，σ²)为加性高斯白噪声。假定多项式系数的阶数为7，FIR滤波器的阶数为3，实验中的参数设置见表1。表1中的两组参数具有很高的相似度，因而仿真产生的两组信号也非常相似，从而保证了实验的有效性。

    实验中基于表1中的参数，仿真分别产生真实发射机和欺骗干扰机各1 000个长度为256的样本信号。分类识别中采用的分类器为支持向量机（SVM），实验中选取真实信号与欺骗干扰各500个样本用于训练，剩余1 000个样本作为测试。设信噪比从-10 dB～20 dB变化，步长为2 dB，最终识别结果由100次实验取平均得到。

    图1为在不同信噪比情况下两种方法在提取不同特征时的识别率对比图。由图1可以看出，欺骗干扰的检测识别准确率随着信噪比的升高而增大。以奇异值为特征时，基于双谱的特征提取算法识别性能较基于DS-CWB的特征提取算法要好，且识别率平均高出5%。利用本文提出的四维特征时，基于DS-CWB的特征提取算法优于基于双谱的特征提取算法，识别的准确率平均高出15%以上，且效果最优。另外，本文提出的基于DS-CWB的特征提取算法在信噪比大于5 dB时，准确率可高达90%以上；在信噪比为0 dB时，准确率也达到82.5%。实验说明，在提取高维的奇异值特征时，双谱有较好的性能，但是在提取低维特征时，DS-CWB性能要远远优于双谱，而本文中提取的特征较奇异值分解计算复杂度低，且低维特征减小了后续分类步骤的计算量，因而具有更大的优势。

3.2 硬件实验

    硬件实验采用三块来自同一厂家的开源软件无线电开发板HackRF one构建实验平台，两块HackRF one分别模拟真实发射机和转发式欺骗干扰机，分时发送相同数据，一块HackRF one作为接收机，在接收端接收并采集数据。信号源为一段44.1 kHz、单通道、wav格式的音频信号，通过4QAM调制发射，信号采样率统一设置为8 MHz，中心频率设置为92 MHz，接收带宽为250 kHz。在Ubuntu系统的GNURadio平台上，通过TCP/IP协议发送，再将接收数据储存到电脑中。

    与软件仿真实验相同，该实验同样采集2 000个长度为256的样本信号，然后使用SVM进行分类识别。训练和分类采用和上述实验相同的设置。不同信噪比情况下的识别准确率如图2所示。图2为采用实测信号分析时，不同信噪比情况下，两种算法在提取不同特征时得到的识别率对比图。当以奇异值为特征时，基于DS-CWB的特征提取算法要优于基于双谱的特征提取算法，且识别率平均高出12%。按照本文算法提取DS-CWB和双谱的四维特征时，基于DS-CWB的特征提取算法优于基于双谱的特征提取算法，识别的准确率平均高出30%以上，且效果最优。在信噪比为-6 dB时，识别率可达80%，在信噪比为6 dB时，识别率接近100%。

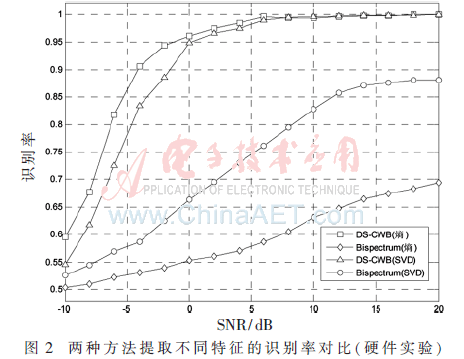
    由以上两个实验可以看出，DS-CWB相较于双谱，在不同类型信号的特征提取方面均有良好的识别性能与稳定性。高维的奇异值特征相较于本文提取的低维特征并无明显优势，而且低维的特征可以减小后续的分类过程的计算量。这进一步证实了本文提取的低维特征在辐射源个体识别中的优势，表明本文基于DS-CWB的特征提取算法在卫星导航信号的欺骗干扰识别中可以取得良好的识别性能，且在应用广义的辐射源识别中也能实现良好的效果。

4 结论

    针对卫星导航欺骗干扰识别问题，本文提出一种基于DS-CWB的特征提取算法。该方法首先计算DS-CWB，进而得到其对角切片谱DS-CWB，然后计算DS-CWB的谱分布熵和奇异谱熵，并结合谱均值、谱对数和构成信号的射频指纹特征向量。该方法不但能有效减小算法复杂度，还能保留大部分有用的WB信息。仿真实验与硬件实验均采用SVM对信号进行分类识别，其结果表明，基于DS-CWB的特征提取算法不仅在识别准确率上要优于基于双谱的特征提取算法，且具有更好鲁棒性。本文特征提取算法也可应用于辐射源个体识别技术中。

参考文献

[1] KENNEDY I，SCANLON P，MULLANY F，et al.Radio transmitter fingerprinting：a steady state frequency domain approach[J].Vehicular Technology Conference IEEE，2008.

[2] WENDT H，ABRY P，JAFFARD S.Bootstrap for empirical multifractal analysis[J].Signal Processing Magazine IEEE，2007，24：38-48.

[3] XU Y，QIAN Z P，SHAO W，et　ａｌ.Radio identification algorithm based on high order spectrum analysis of radio steady-state[C].In Communication Technology(ICCT)，2012 IEEE 14th International Conference on，2012：956-960.

[4] TANG L，JIANG T.Target identification based on diagonal slice of the complex bispectrum[C].In Communication Problem-Solving(ICCP)，2014 IEEE International Conference on，2014：303-306.

[5] GERR N L.Introducing a third-order Wigner distribution[J].Proceedings of the IEEE，1988，76：290-292.

[6] FONOLIOSA J R，NIKIAS C L.Wigner higher order moment spectra：definition，properties，computation and application to transient signal analysis[J].IEEE Transactions on Signal Processing，1993，41：245-266.

[7] CHOI H I，WILLIAMS W J.Improved time-frequency representation of multicomponent signals using exponential kernels[J].Acoustics Speech & Signal Processing IEEE Transactions on，1989，37(6)：862-871.

[8] TANG L，JIANG T.Target identification based on diagonal slice of the complex bispectrum[C].In Communication Problem-Solving(ICCP)，2014 IEEE International Conference on，2014：303-306.

[9] MING W L，DOHERTY J F.Nonlinearity estimation for specific emitter identification in multipath channels[J].IEEE Transactions on Information Forensics and Security，2011(6)：1076-1085.