摘 要： 针对室内复杂环境所引起的NLOS误差，提出了一种利用小波良好抑制噪声特性的室内定位优化算法，选定IEEE 802.15.4a模型为超宽带室内无线定位的普适模型，在室内传统定位算法基础上利用小波去噪消除NLOS误差，从而改进优化了到达时间差定位算法（TDOA）。仿真结果表明，该算法较Chan算法和LS算法定位精度高，具有可行性。
关键词： 超宽带信道；室内定位；非视距误差；小波；到达时间差
0 引言
随着便携智能移动台和可穿戴设备的快速发展和普及，基于位置服务（LBS）的应用场景层出不穷，而保证此类服务质量的前提就是地理位置信息的确定。
室内无法直接使用卫星定位系统进行定位[1]，所以室内无线定位的方式主要有到达时间差定位法（TOA）、时间差定位法（TDOA）、到达角度定位法（AOA）以及混合定位等方法[2-3]。影响定位效果的重要因素之一就是室内环境中普遍存在的NLOS误差，去除这些数据信号中的噪声是提高定位精确度和效率的根本。参考文献[4-5]中采用神经网络优化数据，能较好地抑制NLOS误差，但神经网络算法也存在不足，如固定学习率或学习过程中出现的瘫痪现象会导致训练时间较长；采用了基于误差和性能指标函数不断减小的标准梯度下降法，易导致局部极小值等问题。
本文提出一种利用小波去噪的方法，对室内环境中的NLOS误差进行抑制处理，在获得优化后的数据之后，使用Chan算法进行位置估计，并对该算法进行了仿真，同时与两种经典的算法进行对比，结果表明，本文算法优于上述两种算法。
1 仿真信道模型
鉴于室内环境的特殊性以及室内无线定位的发展趋势，结合超宽带信号相较其他信号抗干扰能力强、穿透性好、低功耗等优点，本文选择IEEE 802.15.4a标准信道模型[6]为本文定位算法的仿真环境。
参考文献[7]介绍了三种室内UWB信道模型（单簇指数模型、簇模型以及指数对数正态模型），其中IEEE 802.15.4a是IEEE提出的新通信标准，特别适用于低速率和低功耗数据传输的场景。此模型是通过修改S-V信道模型，将各径的瑞利幅度分布特性改成对数-正态分布，保证各簇之间的衰落以及簇内各径之间的衰落是互相独立的，且信道满足慢衰落特性，其数学表达式可描述为：
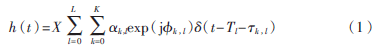
其中，h（t）是一次信道实现，
，l是多径信道系数，Tl是第l簇的时延，τk，l是相对应于第l簇的到达时间Tl内的第k个多径元，X是个对数正态阴影衰落，相位
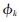，l是在[0，2π]内均匀分布的随机变量。信道系数定义为小尺度衰落系数的积，即：
其中，pk，l 为以等概率取±1的离散随机变量，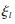
为第l簇的幅度衰减，
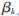，l为第l簇第k径的幅度衰减。测量的数据的幅度特性服从对数-正态分布，而且大尺度衰落也服从对数-正态分布，则有：
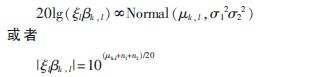
其中，n1和n2分别服从均值为零、方差为
的正态分布，且相互独立，分别对应于每一簇和簇内每一多径的衰落。利用簇幅度和簇内每个多径分量幅度都服从指数衰落的特点，可以得到
，l的值为：
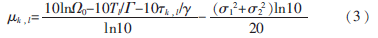
其中，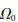
是第一簇第一径的平均能量；
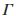是簇能量的衰减因子；
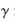是簇内径能量的衰减因子。
根据常见的使用场景和覆盖范围，此次仿真使用CM4信道，其统计特性如表1所示。
2 算法描述
小波分析是在Daubechies提出建立具有紧支撑的光滑小波和Mallat的多分辨分析及快速小波变换之后才有了长足的发展。小波变换可以把信号的能量集中到某些频带的少数系数上。同时，通过把其他频带上的小波系数置零或是给予小的权重，即完成有效抑制噪声的目的。此法计算速度快并且精确度高，所以小波去噪已经成为小波变换的重要应用之一，并被广泛使用在各个领域[8]。
2.1 小波去噪应对NLOS误差的方法
令观察信号s（ti）为ti时刻TDOA的测量值，NLOS误差属于加性误差，所以实验数据s（ti）等于真实值f（ti）和标准测量误差n（ti）与非视距误差nlos（ti）之和，带噪声的信号模型表示如下：
s（ti）=f（ti）+n（ti）+nlos（ti）（4）
其中，n（ti）为零均值的高斯随机变量，nlos（ti）为正随机变量。
结合软阈值和硬阈值去噪方法，其具体步骤如下：
（1）先对含噪的原始信号数据s（ti）作小波变换得到一组小波系数wj，k；
（2）通过对wj，k进行阈值处理，得到估计小波系数j，k，使得‖j，k-uj，k‖尽可能小；
（3）利用j，k进行小波重构，得到估计信号数据（ti），即为去除NLOS信号误差之后的信号数据。
估计小波系数的方法[9]如下：取λ作为阈值（门限），硬阈值估计定义为：
2.2 超宽带信道下的TDOA定位算法（Chan算法）
设MS坐标为（x，y），定位中的参考基站BSi坐标为（xi，yi），数量为M，ri，1是MS到BSi的距离差，c为电波传播速度，根据测量到的电波传播时间（TOA）可建立距离方程：
ri2=（cτi）2=（xi-x）2+（yi-y）2=Ki-2xix-2yiy+x2+y2（7）
由于ri，1=ri-r1，式（7）可改写为：
ri，12+2ri，1r1=-2xi，1x-2yi，1y+Ki-K1（8）
其中，Ki=xi2+yi2，xi，1=xi-x1，yi，1=yi-y1。
令za=[x，y，r1]T为未知量，可以建立线性方程：
h=Gaza（9）
当存在TDOA噪声误差ni，1时，误差矢量表示为：
使用za的值计算新的B矩阵，之后重复进行一次WLS计算，就可得到估计位置。首先计算za的协方差矩阵，za及协方差矩阵为：
其中，Ga0可由式（11）的结果算出。构造新的误差矢量?鬃′为：
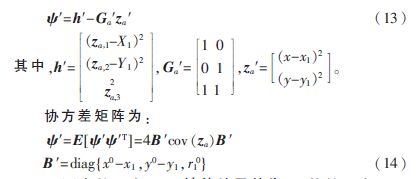
za0可由第二次WLS计算结果替代，za′的第二次WLS计算结果为：
最终，MS估计位置结果为：
2.3 利用小波去噪的超宽带信道下的TDOA定位算法
本文使用小波去噪的方法对在超宽带信道下测到的TDOA数据进行预处理，得到优化的信号数据，最后采用Chan算法进行定位估计，从而得到更加精确的位置信息。具体步骤如下：
（1）在NLOS环境下，通过超宽带无线信道传输方式，获得n组TDOA信号数据，然后再对所测数据进行小波变换得到EMC；
（2）通过2.1节小波去噪方法，确定小波阈值，重构出TDOA信号数据；
（3）对经过小波去噪优化的信号数据，使用2.2节算法最终估计出目标位置的坐标信息。
3 仿真及分析
为了检验本文算法的优化性能，对其进行NLOS环境拟合仿真。仿真的信道环境为超宽带信号IEEE 802.15.4a标准CM4 NLOS信道模型，相关统计参数见表1。其中参考基站位置为7个，且所有BS（参考基站）与MS（移动台）之间存在NLOS误差。选取超宽带信号的覆盖范围和测量误差两个维度进行分析，通过横向对比，从而直观表现出本文新算法的优越性。
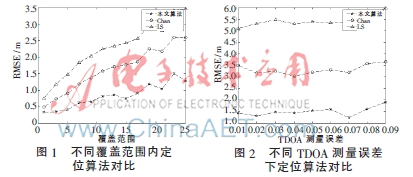
图1为不同覆盖范围下，各定位算法定位结果的均方根误差值仿真图。在超宽带信道下，单纯的Chan算法略优于LS算法，而经过小波去噪处理之后的Chan算法表现出更好的定位精度和稳定性，说明小波去噪对抑制NLOS误差有良好的使用效果。
图2为不同测量误差下三种算法的定位结果比较，纵坐标为不同算法在不同TDOA测量误差下定位结果的均方根误差值。从图中可见，本文算法在原有算法的基础上大幅减小了均方误差的值，并且在不同的TDOA测量误差下，均方误差的值几乎在2以下，表现相当稳定。这说明本文算法在抑制超宽带信道中的非视距误差能力较强，在室内移动台的定位方面效果良好，基于小波去噪的室内定位新算法对原有算法有可替代性。
参考文献
[1] WERB J， LANZL C. Designing a positioning system for finding things and people indoors[J]. IEEE Spectrum， 1998，35（9）：71-78.
[2] Xie Yaqin， Wang Yan， Zhu Pengcheng， et al.Grid search based hybrid TOA/AOA location techniques for NLOS environments[J]. IEEE Communications Letters，2009，13（4）：254-256.
[3] Shen Guowei， RUDOLF Z， REINER S T. Performance comparison of TOA and TDOA based location estimation algorithms in LOS environment[J]. Proceedings of the 5th Workshop on Positioning， Navigation and Communication，WPNC′08， 2008： 71-78.
[4] 毛永毅，李明远，张宝军.一种NLOS环境下的TOA/AOA定位算法[J].电子与信息学报，2009，31（1）：37-40.
[5] 张宝军，毛永毅，白菊荣.一种基于遗传算法径向基神经网络的混合无线定位算法研究[J].西安邮电大学学报，2008，13（3）：25-28.
[6] 王丹，普杰信，杨雷.超宽带无线通信系统信道估计技术[M].北京：科学出版社，2012.
[7] GREENSTEIN L J， GHASSEMZADEH S S， HONG S C，et al. Comparison study of UWB indoor channel models[J]. IEEE Transactions on Wireless Communications， 2007，6（1）：128-135.
[8] 张仁辉，杜民.小波分析在信号去噪中的应用[J].计算机仿真，2005，22（8）：69-72.
[9] 徐晨，赵瑞珍，甘小冰.小波分析应用算法[M].北京：科学出版社，2004.