摘  要： 为了进一步减少多用户MIMO（Multiple-Input Multiple-Output）下行传输系统的误码率，提出了正则块对角化迫零矢量预编码设计（RBD-ZF-VP）。该方法利用正则块对角化预编码（RBD）和矢量预编码（VP）的优点，在原有MIMO系统RBD预编码的基础上，将RBD预编码的矩阵转变成信道等价矩阵，然后利用迫零（ZF）准则求出VP的扰动矢量，再将扰动矢量加到原有信号上构成新信号向量，接着对新信号向量进行处理。仿真结果表明，该方案支持多用户多天线MIMO传输系统，与传统的块对角化（BD）预编码和RBD预编码相比，有效地提升了系统性能，具有显著的系统误码率性能优势。

　　关键词： MIMO系统；多用户MIMO；预编码

0 引言

　　MIMO技术是未来无线通信系统的关键技术。当发射端已知准确的信道状态信息时，预编码处理的目的是改善性能和提高系统容量，可以分为线性预编码和非线性预编码。对于线性预编码，常用ZF[1]和BD方法，参考文献[2]中BD方法通过寻找使等价信道块对角化的预编码矩阵，形成等价的并行单用户多天线信道，各用户间的干扰为零。此时，每个用户可视为独立的MIMO信道，然后采用单用户的信号处理方法。然而，BD技术需要每个接收用户的信道状态信息，在完全消除多用户干扰的同时没有考虑噪声的影响，在中低信噪比区域的系统性能较差。参考文献[3]中RBD算法在抑制多用户干扰的同时考虑噪声的影响，首先均衡噪声与多用户干扰，将多用户MIMO信道分解为单用户MIMO信道，然后对每个子单用户信道做进一步优化处理以获得更优的系统性能，但是在噪声较高的情况下系统预编码的误码率性能较差。非线性预编码主要包括脏纸编码、汤姆林森-哈拉希玛预编码（THP）、VP预编码。参考文献[4]首先提出了基于ZF准则和正则化的VP方法。参考文献[5]针对参考文献[4]中的问题进行了改进，求解了最优的正则化系数，并利用扰动矢量的统计特性重新构造了接收端的信号处理，获得了1.5 dB的性能增益。

　　本文提出RBD-ZF-VP预编码设计，这种预编码算法首先设计RBD预编码，接着提出等价信道，再利用迫零准则设计新方案的预编码矩阵，最后进行矢量预编码设计。在考虑多用户干扰的同时考虑噪声的影响，在发射信号向量调制后，通过ZF准则求出RBD-ZF-VP算法预编码矩阵，接着最小化功率归一化缩放因子ZF计算出用户k的最优扰动矢量，将其线性相加到原始信号上，构成新的信号向量，然后与由ZF准则求得的预编码矩阵相乘获得发射信号。在接收端，通过接收矩阵来均衡接收信号，再使用模运算来消除扰动矢量的作用，最后得到原始信号的估计值。这种算法支持多数据流传输，与传统的BD和RBD预编码算法相比，取得了较好的多样性性能，进一步降低了系统误码率。

1 系统模型

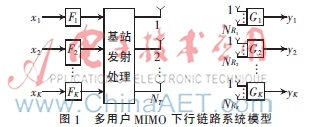
　　MIMO下行多用户链路系统的模型如图1所示。假设基站发射天线数为NT，用户k（k=1，2，3，…，K）的接收天线数为NRk，在系统接收端共有K个用户，所有用户的总接收天线数为：

　　发射信号向量为：

　　x=[x1H，x2H，…，xKH]H∈Cr×1，xk∈Crk×1

　　发射天线到所有接收天线的信道矩阵为：

　　H=[H1H，H2H，…，HKH]H∈CNR×NT，Hk∈CNRk×NT（2）

　　所有用户接收的加性噪声为n=[n1H，n2H，…，nkH]H∈CNR×1。每个元素是独立同分布的，服从均值为零，方差为n2的复高斯分布。

　　本文研究的系统为下行多用户链路系统，所有用户的接收信号为：

　　y=G（HFx+n）（3）

　　其中，y=[y1H，y2H，…，ykH]H∈Cr×1。

　　发射预编码矩阵为：

　　F=[F1，F2，…，FK]∈CNT×r

　　接收均衡矩阵为：

　　G=diag（G1，G2，…，GK）∈Cr×NR

2 RBD-ZF-BD预编码设计

　　引用参考文献[3]与参考文献[6]，在RBD设计方案中，预编码矩阵可以表示为：

　　其中，Fa=[Fa1，Fa2，…，FaK]∈CNT×Nx，Fb=diag（Fb1，Fb2，…，FbK）∈CNx×r。

　　参数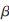满足的功率约束条件为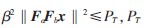：，PT为总发射功率。

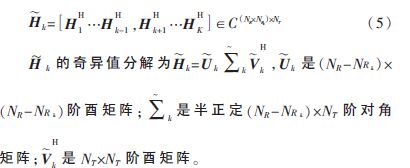
　　优化准则为：

　　每个用户k的预编码矩阵为：

　　Fak=Nak·Dak（7）

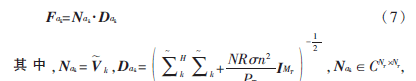　　Dak∈RNT×NT分别为酉矩阵和主对角线大于等于零的功率负载对角矩阵。

　　在RBD预编码设计后，接着进行矢量预编码设计。在矢量预编码中，使用当前用户k的信道和用户k的预编码矩阵根据ZF准则和功率归一化条件计算出扰动矢量，将其线性相加到原始信号上去，构成新的信号向量，然后对其进行预编码，获得发射信号。图2给出了包含矢量预编码的系统传输模型。

　　在发送端分别对每个用户的数据流进行编码，用户k的预编码矩阵为：

　　基于这个预编码矩阵，本文提出新算法的等价信道为：

　　根据这个等价信道，本文利用ZF准则，发射预编码矩阵和等价信道矩阵满足Heff，kF=I，因此预编码矩阵FZF=H，接着使用功率归一化条件，归一化缩放因子为：

　　由于H增强了发送功率，为了减少每个用户预编码信号矢量的标准，提出了发送端应用一个矢量给空间发送多路传输信号矢量，通过最小化?酌ZF，用户k最优扰动矢量为：

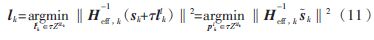
　　在这里k=sk+τllk，sk是在求解扰动矢量前QAM调制后第k个用户的发送信号矢量，lk是第k个用户的扰动矢量，在间隔为τ的整数格τZ2Lk中选取，τ是正整数，τ=（M-QAM星座图），等价于以τ为间隔单位扩展了原始信号的星座图，扩大了发射信号的自由度，降低了发射信号的功率。lk通过最小化功率归一化缩放因子?酌ZF得到。在接收端通过模操作将τlk去除，不影响原始信号的量化解调。由于发送端发送了由于扰动干扰的错误符号，接收到的信号yk=k+nk，k=mod（yk）。

3 仿真结果分析

　　对提出的RBD-ZF-VP预编码与其他预编码方法进行比较，采用多用户多天线下行链路系统，使用符号{Nr，1，Nr，2…Nr，K}×Nt对用户数目和收发天线进行描述，采用4QAM的调制。信道模型采用平坦衰落信道，平坦衰落系数服从均值为0、方差为1的复高斯分布。通过仿真将本文算法与BD、RBD和BD-ZF-VP算法对误码率性能进行比较。图3~图5分别为对收发天线结构为{2，2}×4、{2，4}×6、{3，3}×6的系统进行了比较，分别表示了不同用户接收天线相等、不同用户接收天线不相等的两种情况。

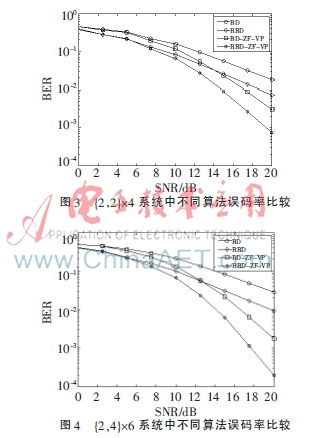
　　格规约算法显著地提高了MIMO系统的分集增益，在下面的仿真图中，新提出的RBD-ZF-BD预编码的误码率性能优势明显，尤其是高信噪比时。在图3和图5中，不同用户接收天线相等时，新算法{3，3}×6的系统的误码率性能优于{2，2}×4系统误码率性能，在接收天线数目增多时，新算法的误码率性能提高显著。在图5中，在误码率为10-2时，RBD-ZF-VP预编码相比传统的BD预编码信噪比降低了近8 dB；在误码率为10-3时，RBD-ZF-VP预编码比BD-ZF-VP预编码信噪比降低了约2 dB，并且随着信噪比的提高，误码率性能越明显。显然，RBD-ZF-VP预编码算法的误码率性能好于其他3种算法，性能较好的原因部分在于基于MMSE准则设计的RBD算法，部分在于矢量预编码本身较大的分集增益。

4 结论

　　本文提出了RBD-ZF-VP预编码算法，该算法支持多用户MIMO系统中多数据流传输，不需要额外的信息交互，相比于BD预编码、RBD预编码、BD-ZF-VP预编码方案，误码率性能显著降低，具有较好的实用价值，是一种适用于多用户多天线下行链路系统的有效算法。

　　参考文献

　　[1] PEEL C B， HOCHWALD B M， SWINDLEHURST A L.    A vector-perturbation technique for near-capa-city multiantenna multiuser communication-part I： channel inversion and regularization[J]. IEEE Transactions on Communication， 2005，53（1）：195-202.

　　[2] SPENCER Q H， SWINDLEHURST A L， HAARDT M. Zero-forcing methods for downlink spatial m-ultiplexing in multiuser MIMO channels[J]. IEEE Transactions on Signal Processing， 2004， 52（2）：461-471.

　　[3] STANKOVIC V， HAARDT M. Generalized design  of multi-user MIMO precoding matrices[J]. IEEE Transactions on Wireless Communications， 2008，7（3）：953-961.

　　[4] HOCHWALD B M， PEEL C B， SWINDLEHURST A L.    A vector-perturbation technique for near-capa-city multiantenna multiuser communication. Part II： perturbation [J]. IEEE Transactions on Communications，2005，53（3）：537-544.

　　[5] YUEN C， HOCHWALD B M. How to gain 1.5 dB in vector precoding[C]. IEEE Global Te-lecommunications Conference， San Francisco，USA， 2006：1-5.

　　[6] CHAE C， SHIM S， HEATH R W Jr. Block diag-onalized vector perturbation for multiuser MIMO systems[J]. IEEE Transactions on Wireless Com-munication， 2008， 7（11）：4051-4057.