摘 要: 为了能够进一步准确地估计出雷达信号的瞬时频率,在原有的Morlet小波基函数的基础上,提出了一种改进的Morlet小波基函数,并将其用于小波脊线的提取。用改进后的Morlet小波基函数来提取雷达信号的小波脊线特征,从而估计出雷达信号的瞬时频率。仿真结果表明,用改进后的Morlet小波基函数提取出来的雷达特征比利用原有的Morlet小波基函数提取出来的雷达特征性能更优,具有更好的时频综合特性及良好的抑制噪声能力,其方法是可行的。
关键词: 瞬时频率;Morlet小波变换;小波脊线
0 引言
在电子情报侦察和对抗领域,能否有效地、高精度地从被截获的雷达信号中提取信号的瞬时参数,对识别信号的“指纹”具有重要的意义[1]。瞬时频率比瞬时幅度具有更强的抗外界干扰的优点,并且它能够反映每一时刻雷达信号的频率变化,因此成了一个研究热点[2-9]。
本文根据Morlet小波参数对信号调制特征的影响及对小波脊线理论的分析[2],提出了一种既有良好的抑制噪声能力又具有综合时-频分辨率较高的小波基函数,用于小波脊线的提取[3],并通过小波脊线迭代方法估计信号的瞬时频率。该方法能够做到连续小波变换的最优尺度选择,比小波变换的模极大值方法更优。
1 小波脊线原理
小波变换的时频平面脊线上分布的参数能用来描述原始信号的重要参数,因为它与原始信号之间具有很强的相似性。而信号的频率与幅度的变化往往由脊线的位置及脊线上分布数据的起伏变化决定的[4]。
1.1 信号的解析表示
数学上,任意实信号s(t)都可以表示成以下的形式:

信号s(t)对应的解析信号可表示为:
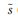 (t)=s(t)+jsH(t)(2)
(t)=s(t)+jsH(t)(2)
其中,sH(t)为信号s(t)的Hilbert变换,且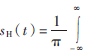
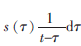 。如果s(t)为渐进信号,即信号的幅度变化要远远小于信号的瞬时频率变化,即:
。如果s(t)为渐进信号,即信号的幅度变化要远远小于信号的瞬时频率变化,即:
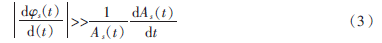
则其解析信号可近似表示为:

在之后的讨论中,把要分析的信号s(t)限定在实Hardy空间:
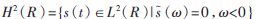
1.2 小波脊线
若(t)=Aε(t)e为实小波ε(t)的解析形式,则渐进信号s(t)的解析小波变换为:
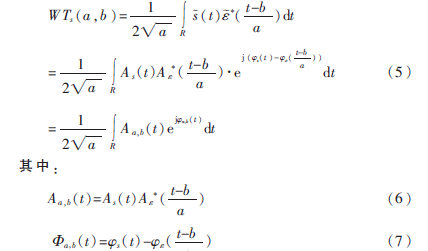
式中*表示复数共轭。由平稳相位原理可知,驻点ts对积分式起着主要的作用。对于单成分的信号而言,在信号(t)及小波函数均为渐进函数的情况下,相位?椎a,b(t)关于时间t就仅仅只有一个驻点ts,即满足′a,b(ts)=0且a,b(ts)≠0。
定义小波脊线为:
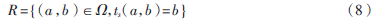
根据驻点的特性,小波脊线上满足:
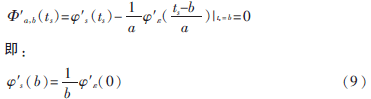
显而易见,尺度a和平移参数b互为函数关系,即有:

小波脊线上有式(10),式中ar(b)即为小波脊线,可以看出小波脊线是平移参数b的函数。由式(10)可知,通过提取小波脊线就可以完成信号瞬时频率fr(t)的提取,如式(11)所示:
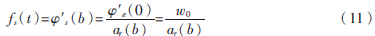
其中,w0为小波基函数的中心频率。
2 小波基函数的选取
为了提取小波脊线,假定信号s(t,r(t))具有随r(t)变化的瞬时性,如果r(t)能够被小波基函数g(t)检测出来,则需要满足以下3个条件[5-6]:
(1)在r(t)=r不存在瞬时变化的情况下,小波系数WTs只随a变化,与b无关,即L(a)=WTs{a,t|r},r为常数;
(2)在t时刻r(t)变化时,WTs{a,t|r}会产生一个明显与L(a)不同的值;
(3)在t时刻,为了达到一个相对比较高的检测频率,小波系数与L(a)的差值D达到最大,即Dmax=max(|WTs(a,t)-L(a)|)。
由小波脊线检测条件知,小波脊线的提取效果与小波基函数的选择有直接的关系。
2.1 Morlet小波
Morlet小波常因为其具有良好的时-频域特征,而被选为提取雷达信号特征参数的小波基函数,它的表达式为:
g1(t)=exp(-t2/N)exp(jw0t)(12)
当N=5时,为普通的Morlet小波,其波形如图1所示。
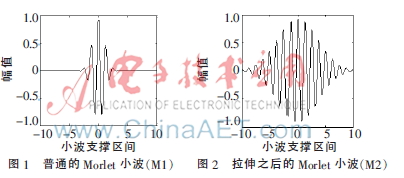
当N=25时,波形如图2所示,它的傅里叶变换为:
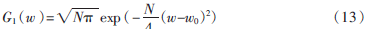
母波时频窗为:
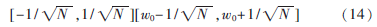
子波时频窗为:
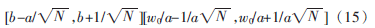
由式(15)可知,小波变换对信号的时频分辨率受到小波原子尺度a的伸缩的直接影响,而b只是对时频窗位置的改变。尺度因子a越小,时域分辨率越高,频域分辨力就越低。为了提高检测概率,小波变换通过调节a的值来满足?驻w,使时频分辨率能够自适应调节。
由式(14)、(15)知,N的作用主要是协调时域和频域的分辨力,使其都达到最优状态。N越大,频率分辨力就越大,但由于N受到小波变换条件及时域分辨率的约束,不可能无限制地增大,因此在估计信号瞬时频率时,要兼顾时域和频域。
2.2 改进的Morlet小波
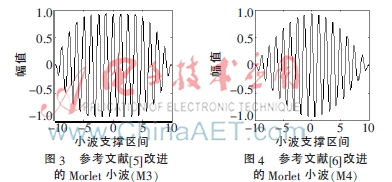
参考文献[5]为了得到较好的检测率,提出了一种新的Morlet小波(波形如图3所示),即:
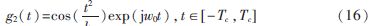
小波基函数的有效支撑区间为[-Tc,Tc];由0≤t2/k≤π/2?圯k=2T2/π。相比式(12)而言,式(16)通过增大N的值,把小波拉伸至类似余弦函数的其中一段。从图2和图3可看出,式(16)虽然有较好的幅频特征,但却使时域分辨率降低了,所以它并没有在整个时频域内使检测概率以及检测精度达到最佳效果。因此,参考文献[6]又对式(16)作了改进(波形如图4所示)。
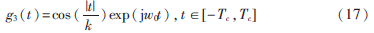
小波基函数的有效支撑区间为[-Tc,Tc],由0≤|t|/k≤π/2?圯k=2T/π。从图4可看出,式(17)的性能优于式(12)和式(14),因为它综合考虑了时频分辨率。
通过分析可以发现Morlet小波的时域包络随着N的增大波形更趋近于一个二项式函数。但由于要综合考虑时频分辨率,而且被容许条件限制着,N的值不可能无限增大。依据上述分析,为达到较高的时频分辨率及高检测率,提出了基于二项式函数的新的Morlet小波基函数,其表达式为:
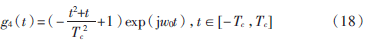
其中,w0为小波中心概率;小波基函数的有效支撑区间为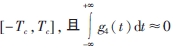 ,近似满足容许条件。设Tc=10时,其波形如图5所示,各类小波基函数的幅频特性如图6所示。
,近似满足容许条件。设Tc=10时,其波形如图5所示,各类小波基函数的幅频特性如图6所示。
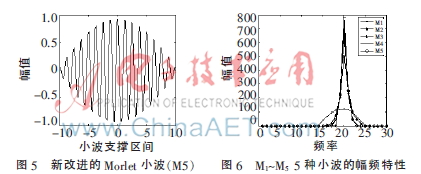
从仿真图可以看出,M1小波虽然有较高的时域分辨率,但是其频域分辨率较差。M5既具有与M2几乎同样的衰减速度,又具有像M3的时域窗口长度、高检测频率和抗噪能力。相比较而言,M5比M3和M4更满足容许条件,M5具有更好的时-频分辨率和高检测频率。图6描述的5类小波的幅频特性中,M1、M2的幅值比M3、M4和M5的小很多;M3的收敛速度比M4和M5的稍差,虽然其幅值最大;而M4和M5则具有同样的收敛速度,但是综合考虑时频分辨率,M5的幅值优于M4,因此M5的幅频特征相对最优。针对渐进信号,用M5对应的小波基函数来提取信号小波脊线特征效果更佳。
3 仿真结果与分析
为验证以上方法的有效性,下面利用上述的5种小波对BPSK和QPSK在信噪比为20 dB的情况下进行小波脊线特征的提取,本文利用的是迭代算法提取小波脊线,即参考文献[7]的算法。信号参数设置如下:载频20 MHz,采样频率80 MHz,编码为7位Barker码,脉宽为10 μs。仿真结果如图7~图11所示。
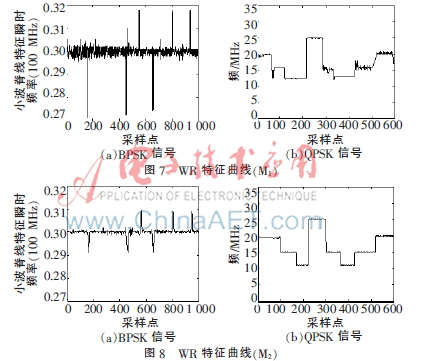
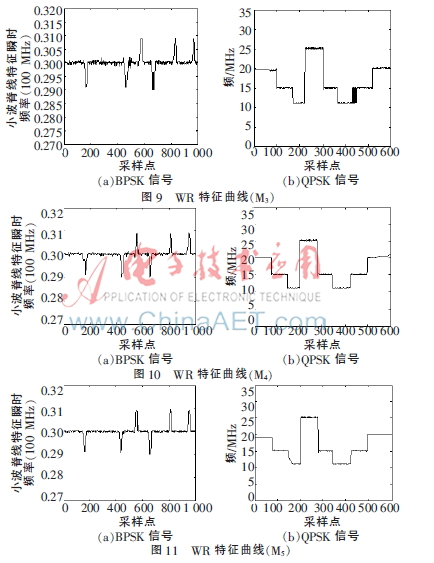
从图7~11可以看出,在噪声环境中,M1的小波脊线特征提取的精确度明显没有其他几个小波脊线的精确度高,M1抗噪性能较差,易受噪声影响。在某些点上,M2、M3、M4的提取精确度没有M5的高。所以综合看来,M5的提取效果比M2、M3、M4的提取效果好,抗噪声能力比较强。从上述仿真结果图可以看出,M5的小波脊线特征提取具有更优良的抑制噪声的能力,能更加准确地估计出信号的瞬时频率。
4 结论
本文在原有的Morlet小波基函数的基础上,通过改良提出了一个新的Morlet小波基函数,用于小波脊线特征的提取,来更加准确地估计出雷达信号的瞬时频率,其理论性和实用性良好。MATLAB仿真结果显示,使用改良版Morlet小波提取出来的雷达信号的脊线特征能更好地抑制噪声的影响,检测概率也有所提高,能更精确地为雷达信号的分选和识别提供依据。
参考文献
[1] DELPART N. Asymptotic wavelet and Gabor analysis extraction of instantaneous frequencies[J]. IEEE Transactions on Information Theory,1992,38(3):644-664.
[2] MALLAT S. A wavelet tour of signal processing[M].San Diego, CA: Academic Press,1998.
[3] 余志斌,金炜东,陈春霞.基于小波脊频级联特征的雷达辐射源信号识别[J].西南交通大学学报,2010,45(2):290-295.
[4] HO K C, PROKOPIW W, CHAN Y T. Modulation identification of digital signals by the wavelet[J]. Transform IEEE Proc-radar naving, 2000,147(4):169-176.
[5] 任春辉,魏平,肖先赐.改进的Morlet小波在信号特征提取中的应用[J].电波科学报,2003,6(18):633-637.
[6] 余志斌,陈春霞,金炜东.一种新的Morlet小波及其在雷达信号特征提取中的应用研究[J].电路与系统学报,2010,15(1):129-134
[7] 王兵,羿旭明.一种提取小波脊线的迭代算法[J].数学杂志,2005,25(3):295-298.
[8] 潘继飞,姜秋喜.一种脉间滑变雷达信号特征提取新方法[J].电子信息对抗技术,2011(1):80-99.
[9] 白航,赵拥军,赵国庆,等.一种改进的雷达信号小波包特征提取方法[J].信息工程大学学报,2012(1):12-14.

