摘  要： 在总结维基百科特点的基础上，调研了国内外使用维基百科计算语义相关度的算法。根据这些算法的特点，对其进行了系统的分类，并列举了每个分类下的经典算法。

　　关键词： 维基百科；相关度；算法

0 引言

　　相关度是指事物之间相关联的程度，而语义相关度是指概念之间相关联的程度。计算语义相关度是非常复杂的，因为它需要用到丰富的语义知识，也要对不同的关系给出不同的权重值。在语义信息处理的相关研究中，很多研究者利用语料库的相关统计信息获取语义相关度信息，也有研究者利用WordNet等语义网络来衡量词或者概念之间的语义相关度。近年来，很多研究都证明维基百科是计算语义相关度的一个好资源。

　　最先利用维基百科进行语义相关度研究的是STRUBLE M和PONZETTO S P[1]，他们把应用在WordNet上效果比较好的一些经典算法应用到维基百科中，实验结果表明，在大数据集上，在维基百科的效果要好于在WordNet的效果。随后，ZESCH J和GUREVYC I[2]对维基百科的分类图和文档图进行了图论分析并与GermaNet进行了比较，同样证明了维基百科可以作为一种语义知识资源代替一些传统的语义网络，将自然语言处理的一些经典算法应用到维基百科中是可行的。

　　本文对维基百科进行了研究，对利用维基百科计算语义相关度的算法进行了调研，最后总结了几种典型算法的特点并进行了分类。

1 维基百科

　　维基百科于2001年被发起，现在，它涵盖了艺术、地理、历史、自然科学等领域，包括了200多种语言的版本，注册用户达5000多万。它作为互联网上最大的最广泛使用的免费的百科全书，拥有超过百万的解释页面，更新速度快。本文从以下两方面对维基百科进行系统的介绍。

　　1.1 维基百科中的条目

　　条目，即页面，是维基百科基本的组成单位。为了提高一致性，条目的编辑需遵循一系列的编辑规则，其主要的规则有以下6条[3]：

　　（1）一个条目只描述一个概念，一个概念只有一个条目与之对应；

　　（2）条目的标题是简洁的短语，类似于传统叙词表中叙词；

　　（3）同义词通过重定向链接连接；

　　（4）消歧义条目为用户提供可选择的多种语义；

　　（5）条目的开始是对主题的简单介绍，第一句定义了概念及其类型；

　　（6）条目中有超链接，这些超链接表示了该条目与其他条目之间的关系。

　　根据这些编辑规则，将维基百科中的条目分为：分类条目、重定向条目、消歧义条目以及解释条目。其中分类条目是维基百科中的分类索引，重定向条目和消歧义条目对应规则（3）和（4），解释条目对应编辑规则（1）。

　　1.2 维基百科中的超链接

　　普通的语料库和网络语料最大的不同点就是网络语料库具有超链接，而超链接提供了一个页面跳转到另一个页面的功能。维基百科就是典型的网络语料库。维基百科链接结构密集，平均每个条目拥有20个超链接，而且超链接还蕴含了丰富的语义信息。一般按照超链接的方向把超链接分为两大类：一类是前向链接，另一类是后向链接。如图1所示，前向链接是指源页面连接另外一个页面的链接，后向链接是指一个页面连接源页面的链接。

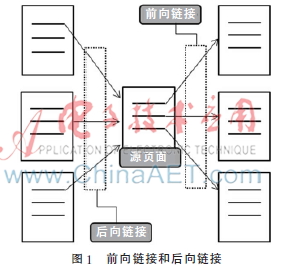
　　除此之外，也可以根据超链接所连接的页面类型进行分类，分别为语言间的链接（Interlanguage Links）、分类与子类之间的链接（Category to Subcategory）、分类与解释页面之间的链接（Category to Article）、重定向页面（Redirect to Article）与解释页面之间的链接（Article to Article）。根据这种分类可以初步判断锚文本之间的关系（锚文本是超链接的文本部分，用户通过点击这个文本就可到达目标页面）。

　　2 基于维基百科的语义相关度算法

　　2.1 基于统计学的语义相关度算法

　　2.1.1 词汇共现法

　　词汇共现法是基于统计学的方法来计算语义相关度的经典方法。由于词汇共现在叙词表构建的研究中已经被广泛地证明是有效的，因此把它应用到维基百科中可能也是可行的。两个词汇的词汇同现率可以用下面的公式进行粗略的定义：

　　其中，D是包含t1的文档的集合。为了度量两个词的相关度，该方法使用了包含这两个词的文档数。具体的比较经典的方法有共现文档数方法（SD）[4]、文字覆盖法（TO）。

　　共现文档数就是在一个较大的语料库中利用词出现的文档数，如Jaccard公式：

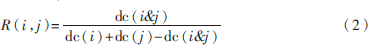
　　其中，dc（i）、dc（j）分别表示包含链接i、j的文档数，dc（i&j）表示既包含i也包含j的文档数。

　　文字覆盖法就是通过在2个词各自的定义文本中共同出现的文本来计算相关度。比较经典的算法有Lesk算法[5]。在维基百科中，可以寻找在解释文档中的共现词并利用式（3）来计算：

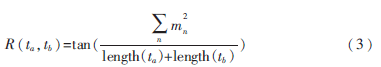
　　其中，n表示文档ta和tb中都出现的文本片段（可能是一个词或连续的多个词），mn表示每个片段的词数，length（ta）和length（tb）表示两个文档的总词数。

　　2.1.2 链接共现法

　　尽管上文中的词汇共现法已被证明是有效的，但是由于语义分析的复杂性，自然语言处理仍然存在很多准确性的问题。所以有人提出了链接共现的方法，这种方法只使用语义网络中的链接来避免自然语言处理中的准确率的问题。因为语义网络是一个概念与链接的集合，所以使用链接同现法是有意义的。具体的公式和词汇共现的公式的道理是一样的，不同点只是使用文档的链接代替词汇。

　　比较经典的链接共现的方法是GABRILOVICH E[6]提出的TF-IDF的方法。TF-IDF使用了两个度量值：TF（Term Frequency）词汇频率和IDF（Inverse Document Frequency）后向文档频率。这种方法是通过计算维基百科页面中链接的权值得到相应概念的向量，然后通过比较概念向量来计算两个概念的相关度。一个文档中链接的权值的计算公式如下：

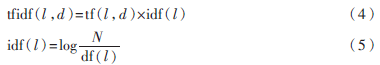
　　其中，tf（l，d）表示在文档d中链接l出现的次数，N表示维基百科中文档的数量，df（l）是包含链接l的文档的数量。简单来说，权值随着文档d中链接出现的频率递增。但是总的来说，因为每个维基百科的页面都有自己的URL而且都对应了一个概念，所以计算两个链接的相关度等同于计算两个概念的相关度。

　　2.2 基于维基百科路径的语义相关度算法

　　维基百科网络词汇集，是一个由条目和超链接组成的集合，它的结构是一个有循环的图，概念就是图的节点，超链接就是图的边，所以它就可以用一个图的形式来表示：G={V，E}（V：维基百科中的条目/概念集合，E：维基百科中超链接的集合）。在考虑如何计算任意一个条目对vi和vj之间的相关度时，NAKAYAMA K等人[7]假设影响它们之间相关度主要有以下两个因素：

　　（1）从条目vi到条目vj的路径的数量；

　　（2）每一条从条目vi到条目vj的路径长度。

　　如果有很多路径可以从条目vi到达条目vj，那么它们之间的相关度相对较强。另外，两个条目之间的相关度还受路径长短的影响。换句话说，如果在图G中从条目vi到达条目vj的路径相对较短，那么它们之间的相关度要高于相对较长的。因此，如果从条目vi到达条目vj的所有路径为P={p1，p2，...，pn}，NAKAYAMA K将它们之间的PF（Path Frequency）定义为：

　　其中，d（lenpk）是一个以路径pk的长度为变量的单调递增函数，例如对数函数的单调递增函数都可用作函数  d（lenpk）。

　　而且根据统计发现，在计算相关度时必须考虑维基百科的链接结构的分布特征，例如这样一种条目，有很多条目都拥有到达该条目的超链接。如果只是用PF的方法，那么这类条目会与很多条目具有较强的相关度。然而通常情况下该类条目对应的概念是普通的比较综合的大众的概念。因此，必须考虑这类条目的后向链接，NAKAYAMA K定义了IBF（Inversed Backward Frequency），IBF与PF组合形成了PF-IBF方法：

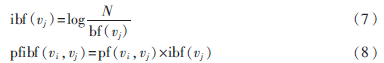
　　其中，N表示所有的条目数，bf（vj）表示条目vj的后向链接数。从上文的PF-IBF公式可以看出，如果条目vi和vj条目通过前向或后向链接相连并且vj没有后向链接，则相应的pfibf值就会很高，概念之间的相关度相对较大。

3 结论

　　维基百科作为世界上最大的在线百科全书，蕴含了丰富的语义知识。本文总结了利用维基百科完成复杂的语义相关度计算的方法，使用这些算法可以更容易地完成对维基百科的知识挖掘和完成文本分类等工作。但目前，无论是对维基百科使用的研究，还是维基百科相关算法研究，我国都远远少于国外。今后，随着维基百科的优势显现，相信会有更多的国内专家关注维基百科，维基百科的相关技术也会更加成熟。

参考文献

　　[1] STRUBE M， PONZETTO S P. WikiRelate! Computing semantic relatedness using Wikipedia[C]. AAAI， 2006，6： 1419-1424.

　　[2] ZESCH T， GUREVYCH I. Analysis of the Wikipedia category graph for NLP applications[C]. Proceedings of the TextGraphs-2 Workshop （NAACL-HLT 2007）， 2007：1-8.

　　[3] MEDELYAN O， MILNE D， LEGG C， et al. Mining meaning from Wikipedia[J]. International Journal of Human-Computer Studies， 2009，67（9）：716-754.

　　[4] BANERJEE S， PEDERSEN T. Extended gloss overlaps as a measure of semantic relatedness[C]. IJCAI， 2003，3：805-810.

　　[5] LESK M. Automatic sense disambiguation using machine readable dictionaries： how to tell a pine cone from an ice cream cone[C]. Proceedings of the 5th Annual International Conference on Systems Documentation， ACM， 1986：24-26.

　　[6] GABRILOVICH E， MARKOVITCH S. Computing semantic relatedness using Wikipedia-based explicit semantic analysis[C]. JCAI， 2007，7：1606-1611．

　　[7] NAKAYAMA K， HARA T， NISHIO S. Wikipedia mining for an association Web thesaurus construction[M]. Web Information Systems Engineering-WISE 2007， Springer Berlin Heidelberg， 2007： 322-334.