摘 要: 在现代电磁工程中,对于边界不复杂的问题,可用解析法得到精准解,但较复杂的边值问题用解析法不能得到解答,需要数值法。在此导出HALLEN方程法,用MATLAB软件实现,它能够非常接近解析值,说明其正确性。矩量法是求解电磁场边界值问题中一种行之有效的数值方法,利用矩量法将HALLEN法的积分方程化为差分方程,将积分方程中积分化为有限求和,从而建立代数方程组,用MATLAB编程进行数值计算和仿真。最后得出结论,矩量法分析能够接近其解析解,说明其正确性。
0 引言
自赫兹和马可尼发明了天线以来,天线在社会生活中的重要性与日俱增,如今已成不可或缺之势。天线是人们见闻世界的耳目,是人类与太空联系的纽带,是文明社会的组成要素[1]。
矩量法是求解电磁场边界值问题中一种行之有效的数值方法,其数学本质是一种求解线性方程的方法[2]。矩量法[3-4]所做的工作是将积分方程化为差分方程,或将积分方程中的积分化为有限求和,从而建立代数方程组,故它的主要工作是用计算机求解代数方程组,因而在电磁场数值计算方面得到了广泛的应用,并已得到了国内外学者的公认。HALLEN E在1938年提出积分方程法[5-6],首先从假定的电流分布用矢量磁位写出天线表面外部的电场公式,然后令此电场等于天线表面内部因克服集肤效应引起的阻抗所需要的电场强度,由此求得表示电流分布的积分方程式。国内外对半波天线的研究主要集中于激励原理、特性、实验等方面的讨论,而关于天线方向图和电流分布等参数计算和分析很少。张黎明[7]、姜光兴[8]等人利用矩量法对半波天线的参数进行了计算。HAFIANE A等人[9]利用天线阵模型对天线的参数进行了计算。基于以上的研究,本文利用HALLEN方法计算并仿真出半波天线的电流分布、功率增益和方向图,计算过程中不但简化了数值分析的复杂性,而且减小了计算量并提高了其精度。
1 天线的关键参数推导
1.1 矩量法的数学表述[7,10]
设一个非其次方程为:
L(f)=g(1)
其中,L为微分算子或积分算子,f为待求的场量或响应,g为已知的源或激励。
设空间为线性的,在算子L的定义域内选择一组函数{fn},将待求函数f展开为它们的组合:

其中,an为待求系数,fn称为基函数或展开函数,由自己选定。将式(2)代入式(1),并因L为线性算子,可得:

在L域内选择一组加权系数(或称检验函数)W1、W2、L、Wn的集合{Wm},并对每个Wm取式(3)的内积,可得:
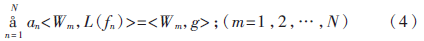
式(4)可写成如下的矩阵形式:
[Lmn][an]=[gm](5)
其中:[Lmn]=<W1,Lf1> … <W1,Lfn> … … …<Wm,Lf1> … <Wm,Lfn>(6)
[an]=[a1,a2,…,an]T,[gm]=[<W1,g>,<W2,g>,…,<Wm,g>]T(7)
如果[Lmn]有逆矩阵存在,记为[Lmn]-1,则待求系数an可由下式解得:
[am]=[Lmn]-1[gm]
于是可将f写成f=[fn][am]=[fn][Lmn]-1[gm]。
1.2 方向图
将方向性函数以曲线方式描绘出来,称之为方向图。它是描述天线辐射场在空间相对分布随方向(q,f)变化的图形,通常指归一化方向图。
(1)立体方向图
变化q和f得到的方向图为立体方向图,它综合描述了天线在各个方向上的辐射情况。
(2)E面、H面方向图
E面是包含最大辐射方向的电场矢量所在的平面。用E面去截取立体方向图,则得到E面方向图。
H面是包含最大辐射方向的磁场矢量所在的平面。用H面去截取立体方向图,则得到H面方向图。
1.3半波对称天线

由于半波天线是特殊的对称天线,因此在这里先介绍对称天线的概念,导出对称天线的参数。
对称天线由两臂长各为l、半径为a的直导线或金属管构成,如图1所示,它的两个内端点为馈电点。对称天线是一种应用广泛的基本线形天线,它既可单独使用,也可作为天线阵的组成单元。
对称天线上的电流分布为:
I(z)=Isin[k(l-|z|)],|z|<l
=Isin[k(l-z)],0<|z|<lIsin[k(l+z)],-l<|z|<0(8)
故对称天线的辐射场为:
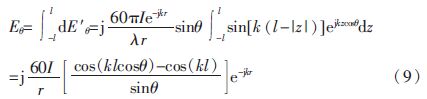
可见,对称天线的归一化方向性函数为:
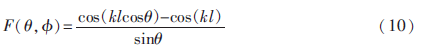
1.4 功率增益
天线增益用来衡量天线对某一特定方向的收发信号的能力,定量地描述某一天线将输入功率集中辐射的程度[11]。在相同距离和相同输入功率的条件下,天线在最大辐射方向上的辐射功率密度Wmax和理想无方向性天线的辐射功率密度之比以G表示,即:
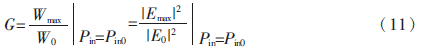
其中,Pin是实际天线输入功率,Pin0是理想无方向性天线的输入功率。
对于有耗情况:Wr=hAWmax,Pr=hAPin。
此时增益表达式可以写成:
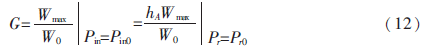
得到天线增益与方向系数的关系为:
G=hAD(13)
天线的有效辐射功率可以表示为:
Pe=PinG=PinhAD=PrD(14)
1.5 电流分布
从前面的介绍可知,HALLEN法从积分方程求解天线的电流分布,知道了电流分布和加在输入端上的电压。
2 仿真结果与分析
前面用HALLEN方法计算出了半波天线的电流分布、功率增益和方向图参数的表达式,最后用MATLAB编程进行数值计算和可视化[12]。
2.1 电流分布
用MATLAB仿真,结果如图2所示。
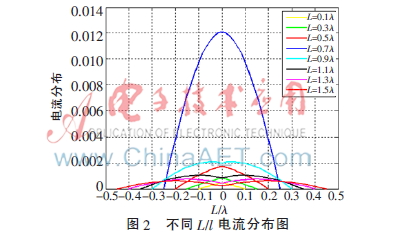
由图2可知,半波振子天线L/l=0.5的电流分布最大,馈点电流最大,辐射电阻近似等于输入电阻,因为半波振子的输入电流正好是波腹电流。
2.2 方向图
将方向性函数以曲线方式描绘出来,称之为方向图。它是描述天线辐射场在空间相对分布随方向(q,f)变化的图形[8,13]。
E面方向图(二维)如图3所示。
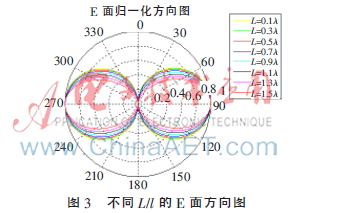
H面方向图(二维)如图4所示,归一化的H面方向图如图5所示。
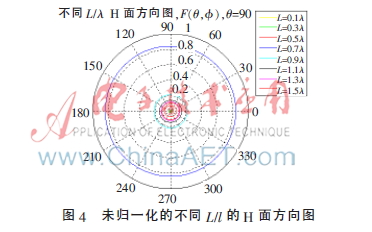

结果分析:
(1)q=0时,辐射场为0。
(2)当L/l<<1(短振子)时,方向函数和方向图与电流元的近似相同。
(3)L/l<1.25时,主瓣随L/l增大变窄。L/l>1后开始出现副瓣(由图4可以看出)。
(4)L/l>1.25时,随L/l增大,主瓣变窄变小,副瓣逐渐变大;L/l继续增大,主瓣转为副瓣,而原副瓣变为主瓣,见图5。
2.3 功率增益
在本文的1.4节介绍了天线的增益,这里直接给出仿真结果,如图6所示。
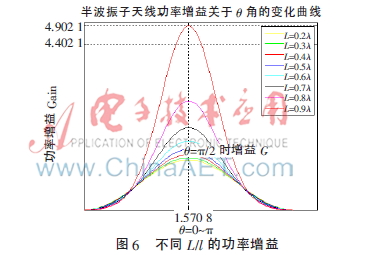
从图6可以看出,半波振子即为L=0.5l,观察L= 0.5l的这条曲线可知,增益半波振子的增益G=1.646 1。
3 结论
本文利用HALLEN方法计算半波天线的电流分布、功率增益和方向图,利用矩量法将HALLEN法的积分方程化为差分方程,将积分方程中积分化为有限求和,从而建立代数方程组,最后用MATLAB编程进行数值计算和可视化。
参考文献
[1] 谢处方,邱文杰.天线原理与设计[M].陕西:西北电讯工程学院出版社,1985.
[2] 曹伟. Method of moments analysis for wire Antennas[Z]. 南京:南京邮电学院,2005.
[3] 刘学观,郭辉萍.微波技术与天线[M].西安:西安电子科技大学出版社,2001.
[4] 徐立勤,曹伟.电磁场与电磁波理论[M].北京:北京邮电大学出版社,1999.
[5] SHAMSI M, RAZZAGHI M. Solution of Hallen′s integral equation using multiwavelets[J]. Computer Physics Communica-tion, 2005,168(3):187-197.
[6] HALLEN E. Theoretical investigation into the transmitting and receiving qualities of antennas[J]. Nova Acta Social Sciences, 1938,3:1-44.
[7] 张黎明,邓阿丽,赵燕平.矩量法计算半波振子天线电流分布[J].舰船电子工程,2006(2):127-129.
[8] 姜光兴,曹伟,朱洪波.基于不同积分方程的线天线矩量法分析[J].南京邮电学院学报,2005,25(1):46-50.
[9] 吴晓英,刘学观.线天线辐射特性的矩量法分析[J].苏州大学学报(工学版),2005,25(3):29-32.
[10] 梁荣江.基于MATLAB分析矩量法在线天线中的应用[J].西安邮电学院学报,2009,14(1):49-56
[11] 陈炜峰,胡蓉,余莉.基于HFSS球形偶极子辐射天线的结构优化[J].扬州大学学报(自然科学版),2013,16(2):52-56
[12] 张志涌.精通MATLAB6.5版[M].北京:北京航空航天大学出版社,2003.
[13] 吕英华.计算电磁学的数值方法[M].北京:清华大学出版社,2006.

