摘 要: 大数据时代悄然而至,数据质量也引起人们的关注。在提高数据质量方面,很重要的一部分是解决数据不一致性问题。针对大数据情况下的数据不一致问题,本文提出了在MAP-REDUCE框架下的聚类算法。本文在MAP-REDUCE框架下对K-MEDOIDS聚类算法进行了改进,增强了算法的适用性和精确性,并通过仿真实验验证了在大数据环境下该算法的并行性和有效性。
关键词: 大数据;数据质量;数据不一致性;MAP-REDUCE;聚类算法
0 引言
随着大数据时代的到来,庞大的数据被赋予了新的生命,而数据质量问题也引起了越来越多的关注。数据质量涉及数据的一致性、正确性、完整性和最小性等多个方面[1-2]。当分布在多个节点的数据集成时,若提供的数据出现重叠,容易引起数据不一致性的问题。如何从若干个不一致的数据中获得理想的数据答案在数据清洗中就显得至关重要[3]。
本文提出了基于MAP-REDUCE的聚类算法解决大数据环境中数据不一致性问题。改进了K-MEDOIDS聚类算法,提高了算法的适用性和精确性。
1 相关工作
目前,解决数据不一致性问题的方案很多,如参考文献[4]讨论了太阳黑子探测数据不一致性问题,并提出了一种加权匹配技术减小数据的不一致性。针对数据复制时产生的数据不一致问题,参考文献[5]定义了不同版本数据的距离函数,以此消除复制数据时的不一致性。参考文献[2]是通过属性间的条件依赖(CFD)探测数据间的不一致性进而进行数据修复。然而,当数据量急剧增大时,现有的清洗算法将不再适用。
在大数据环境下,数据呈现规模性、多样性、高速性和价值性等多种特性[6]。聚类算法是研究分类问题的一种统计分析方法,基于MAP-REDUCE的聚类方法可以有效解决大数据环境中的一些问题。神经网络[7]、贝叶斯网络[8]等算法也都在MAP-REDUCE框架下实现了并行化。
K-MEDOIDS聚类算法介绍如下。
算法1:K-MEDOIDS聚类算法
Initialize:Random k objects in D as medoids
Associate each object to the closest medoid
For each medoid m
For each non-medoid object o
Get DISi
Select the new medoid with the lowest distance
Repeat steps 2 to 6 until there is no change in the medoids
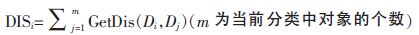
其中,GetDis(Di,Dj)函数的功能是获取对象Di和Dj之间的距离。本文主要解决文本型数据的不一致性问题,所以选择文本的最小编辑距离函数,即Levenshtein距离。
2 基于MAP-REDUCE的聚类算法
2.1 基于MAP-REDUCE的K-MEDOIDS算法
互联网的进步让人们足不出户就可以完成火车票、汽车票、机票等的订购,享受网上购物的乐趣,而这一切,也需要通过在各个网站注册并保留个人身份信息,包括网上银行等,才能完成这一系列操作。假设将这些网络的身份信息汇总到一起,就有可能出现数据不一致情况,如表1所示,T1~T7共7条含有身份证号和姓名的数据来自5个不同的网站,由于某些原因,如拼写错误(T3、T4、T6)、字段截取(T5)等,产生了数据不一致问题。现在定义一条数据的格式为<KEY,VALUE>,如<ID,NAME>。数据集DATA含有n条数据:{DATA1,DATA2,…,DATAn},即{<KEY1,VALUE1>,<KEY2,VALUE2>,…,<KEYn,VALUEn>}。DATA中的数据分布在不同的节点上,当数据集成时,利用MAP-REDUCE框架的MAP过程把具有相同KEY的数据分配到同一节点上,就得到了具有相同KEY值的数据<KEY,List<VALUE>>,如表2和表3所示。
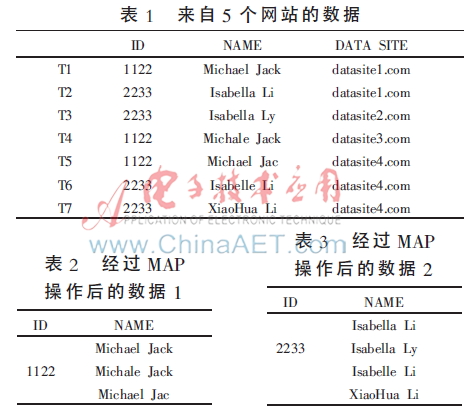
当发现List<VALUE>中的数据不同时(表2、表3),就出现了数据不一致情况。若想在List<VALUE>中找到比较理想的数据,可以采用K-MEDOIDS聚类算法。
把K-MEDOIDS聚类算法应用到MAP-REDUCE框架下,算法如下。
算法2:基于MAP-REDUCE的K-MEDOIDS算法
(1)Input:DATA
(2)Map(DATA)MAPDATA={<KEY1,List<VALUE1>,<KEY2,List<VALUE2>,…}
(3)For each MAPDATA <KEY,List<VALUE>
(4)Get medoids by using K-MEDOIDS algorithm
(5)Get the max-count medoid
(6)Output:<KEY1,VALUE1>,<KEY2,VALUE2>,…,<KEYm,VALUEm>
首先,通过MAP操作把数据集具有相同KEY值的VALUE聚集在一起。然后,通过K-MEDOIDS算法把List<VALUE>中的数据分为K个类,有效排除数量少但误差过大的数据,对于数量较多且误差较小的数据,取其对象最多的分类的中心点作为理想数据。
2.2 更加适用的E-MEDOIDS聚类算法
算法2中,首先设定分类个数为K,然后取随机值作为K个分类的中心点。但在具体应用中,不容易确定K的具体取值。针对此情况,对K-MEDOIDS进行了初步的改进,提出了初始误差值E,以改进聚类初始化时的中心点分布。
算法3:基于MAP-REDUCE的E-MEDOIDS聚类算法
(1)Input:DATA{DATA1,DATA2,…,DATAn}
(2)Map(DATA)MAPDATA={<KEY1,List<VALUE1>,<KEY2,List<VALUE2>,…}
(3)For each MAPDATA<KEY,List<VALUE>
(1)M1=VALUE1
(2)For each non-medoid object o
(3)If GetDis(o,medoids)>E,M.Add(o)
(4)Associate each object to the closest medoid
(5)For each medoid m
(6)For each non-medoid object Di
(7)Get DISi
(8)If DISi=min(DIS)
(9)m=Di
(10)Repeat steps 11 to 16 until there is no change in the medoids
(11)Get the max-count medoid
(12)Output:<KEY1,VALUE1>,<KEY2,VALUE2>,…,<KEYm,VALUEm>
算法3与算法2的不同之处在于(8)~(10)行:首先选取List<VALUE>的第一个值作为第一个分类的中心点(M1)。然后遍历余下的对象,若此对象与所有分类的中心点距离均大于初始误差值E,则把此对象作为新类的中心点添加到Medoids中。算法3用若干分散的对象作为分类的中心点代替算法2中的随机对象,目的是让中心点分布得更加离散,聚类的速度也有所提高。而且用E代替K更适用于本领域,同时还可以通过对初始误差值E的设定控制每个分类的范围。
2.3 具有权重值的EW-MEDOIDS聚类算法
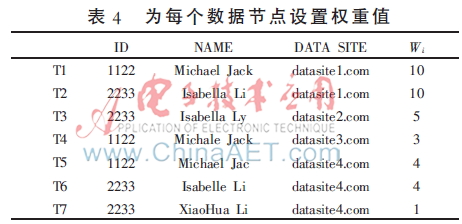
算法3中,把所有节点的数据视作等价的,没有权重大小的区别。然而现实生活中并非如此。例如,政府网站提供的数据往往比其他的网站具有更高的可信度。因此,在所有节点上加上权重值,以此表明此节点数据的可信度。通过权重值的设置,可以调整分类中心点的偏移,使得结果更加精确,如表4所示。
算法4:基于MAP-REDUCE的EW-MEDOIDS聚类算法
(1)Input:DATA
(2)Map(DATA)MAPDATA={<KEY1,List<VALUE1>,<KEY2,List<VALUE2>,…}
(3)For each MAPDATA<KEY,List<VALUE>
(4)M1=VALUE1
(5)For each non-medoid object o
(6)If GetDis(o,medoids)>E
(7)M.Add(o)
(8)Associate each object to the closest medoid
(9)For each medoid m
(10)For each non-medoid object Di
(11)Get DISi with weight
(12)If DISi=min(DIS)
(13)m=Di
(14)Repeat steps 11 to 16 until there is no change in the medoids
(15)Get the max-count medoid
(16)Output:<KEY1,VALUE1>,<KEY2,VALUE2>,…,<KEYm,VALUEm>
数据集D={D1,D2,…Dn}来自若干个不同节点。通过评价节点的可信度,人工设定节点的权重值分别为(W1,W2,…,Wn)。这样数据集D可以表示为{<D1,W1>,<D2,W2>,…,<Dn,Wn>}。算法3和算法2的不同之处在于(13)行,即更新中心点时,权重值属性参与了计算。
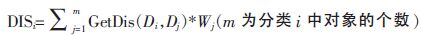
3 仿真实验
为了评估本文提出的算法的效率、并行程度,搭建了HADOOP平台进行实验。实验的编程语言采用Java语言,在HADOOP平台上实现算法1、算法2和算法3。实验平台包含6个节点,每个节点安装有UBUNTU 14.10操作系统、HADOOP 2.4.0平台,具有AMD 3.10 GHz双核处理器和4 GB内存。
本实验数据要求文本型数据,而且其中部分数据呈现错乱现象,因此采用人工生成的测试数据集。具有权重值的EW-MODOIDS算法是在E-MEDOIDS算法的基础上加上节点的权重值控制中心点的偏移,因此只要权重值的设定符合实际情况,EW-MEDOIDS算法的精确性就大于无权重干预的K-MEDOIDS算法和E-MEDOIDS算法,无需实验验证。
3.1 单节点数据规模对运行时间的影响
为了评估算法的运行效率,生成100~1 000条不一致的数据分别用K-MEDOIDS算法和E-MEDOIDS算法(EW-MEDOIDS算法和E-MEDOIDS算法效率相当)在单一节点实现。在生成单节点实验数据时,首先设置固定词条作为正确答案,然后按一定比例随机挑选数据条目进行增加、删除、修改、调换顺序等操作,每组实验数据均取十次相同重复实验结果的平均值。
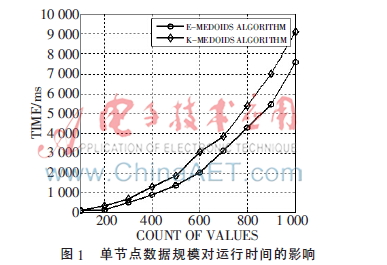
E-MEDOIDS算法中参数E的引入不仅提高了聚类算法的适用性,而且从图1可以看出,E-MEDOIDS算法的运行效率比K-MEDOIDS算法有一定的提高。
3.2 参数E对算法的影响
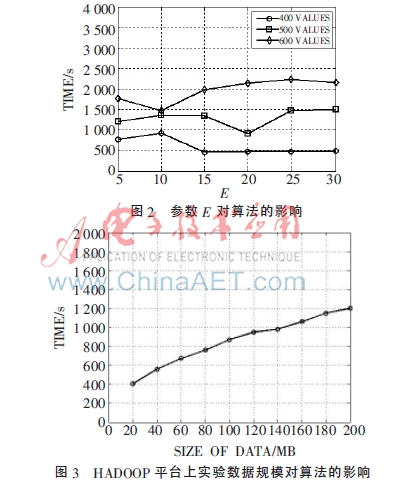
分别采用400、500、600条目的数据集进行实验,每次实验更改参数E的大小,然后收集程序的运行时间。图2表明E-MEDOIDS参数E对算法的运行效率整体影响不大,但是当参数E取得某一恰当值(约等于固定词条的长度)时,程序运行时间取得最小值。因此,正确设置参数E,可以提高算法的效率。
3.3 HADOOP平台上数据集规模对算法的影响
为了验证在大数据环境下算法的并行性,在HADOOP平台上使用大小不等的10组数据进行实验。实验数据集由不同数量的单节点实验数据组成,生成的实验数据文件大小从20 MB~200 MB不等。HADOOP实验平台运行20个MAP-REDUCE任务,实验结果如图3所示。
由图3可以看出,随着数据量增加,HADOOP任务运行时间也平缓增加。当数据量较小时,算法运行时间增长较快;当数据量较大时,运行时间增长比较缓慢。这是因为当数据量较大时才能发挥HADOOP平台下算法并行运算的优势,因此算法具有良好的并行性。所以本文提出的基于MAP-REDUCE的聚类算法可以有效解决大数据环境下数据不一致性问题。
4 结束语
大数据环境中,提高数据质量也将成为数据价值再创造的关键之一。当分布在不同节点上的数据集成时,很容易引起数据不一致问题,严重影响数据质量。本文提出了基于MAP-REDUCE的聚类算法解决大数据环境下的数据不一致问题。通过改进K-MEDOIDS算法提出E-MEDOIDS算法,使聚类算法在处理数据不一致问题上适用性更强。又提出了EW-MEDOIDS算法,引入节点的权重值对聚类算法进行干预,进一步提高聚类算法的精确性。而算法采用MAP-REDUCE框架实现,有效增强了聚类算法的并行性,可高效解决大数据环境下的数据不一致问题。
目前,EW-MEDOIDS算法的权重值是通过人工设定的。当数据节点量很大时,人工设置的方法将不适用。未来可以在自动设置权重值方面开展工作,尽量减少不必要的人工操作。
参考文献
[1] AEBI D, PERROCHON L. Towards improving data quality[C]. CiSMOD, 1993: 273-281.
[2] FAN W, GEERTS F. Foundations of data quality management[J]. Synthesis Lectures on Data Management, 2012,4(5):1-217.
[3] RAHM E, DO H H. Data cleaning: problems and current approaches[J]. IEEE Data Eng. Bull., 2000,23(4):3-13.
[4] SHAHAMATNIA E, DOROTOVI I, MORA A, et al. Data inconsistency in sunspot detection[C]. Intelligent Systems′ 2014, Springer International Publishing, 2015:567-577.
[5] DANILOWICZ C, NGUYEN N T. Consensus methods for solving inconsistency of replicated data in distributed systems[J]. Distributed and Parallel Databases, 2003,14(1): 53-69.
[6] 孟小峰,慈祥.大数据管理:概念,技术与挑战[J].计算机研究与发展,2013,50(1):146-169.
[7] KUMAR V V, DINESH K. Job scheduling using fuzzy neural network algorithm in cloud environment[J]. Bonfring International Journal of Man Machine Interface, 2012,2(1):1-6.
[8] TEWARI N C, KODUVELY H M, GUHA S, et al. MapReduce implementation of variational bayesian probabilistic matrix factorization algorithm[C]. Big Data, 2013 IEEE International Conference on. IEEE, 2013:145-152.

