摘  要： 提出了一种新型两步式迭代最近点算法对三维人耳点云模型进行配准，该过程主要分为两步完成：（1）采用基于CUDA并行加速的ICP" title="EM-ICP" target="_blank">EM-ICP算法进行初始配准，从而使人耳点云数据大致调整为同一姿态，并且为下一步提供良好的初始变化；（2）基于ICP算法对三维人耳点云数据进行精确配准。该方式能够有效避免ICP算法配准过程中局部对齐等缺陷。实验结果证明，采用两步式迭代最近点算法配准后的三维人耳数据具有良好的配准效果与配准速度。

　　关键词： EM-ICP；ICP；人耳；点云配准；CUDA

0 引言

　　在当今信息化时代，随着科学技术的不断发展，传统的基于身份证、学生证、磁卡等的身份鉴别技术存在容易被伪造、被盗取以及容易遗失等问题，暴露出越来越多的缺陷。它们已经不能满足人们对快速、便捷、有效的身份识别技术的需求。在此情况下，生物特征识别技术应时而生。人耳识别是以人耳作为识别媒介来进行身份的鉴别，是一种很有发展潜力的生物特征识别技术，受到了国内外众多研究机构的广泛关注。研究指出，没有任何两个人（即使是双胞胎）的耳朵是完全一样的，并且在8~70岁之间都不会有显著的变化，可以作为个体生物识别的依据。人耳形状特征很丰富，其表面具有大量的沟和脊，不受胡须、化妆品、年龄、表情等影响，具有更高的稳定性、唯一性和健壮性，为人耳识别技术提供了理论研究价值和实际应用前景。

　　随着三维扫描技术的迅速发展，三维数据的获取变得更加方便，三维模型已经成为继数字音频、数字图像、数字视频之后一种新的数字媒体形式。三维人耳模型包含的特征信息比二维图像更为丰富，因此基于三维人耳的识别技术便逐渐发展起来。三维人耳模型不但能够很好的反应人耳的轮廓信息，而且能够很好地描述人耳的结构和姿态信息。采用三维人耳数据进行识别能有效解决姿态变换、阴影和光照条件改变等问题对识别率的影响，因此更适合采用三维的方式来进行采集和识别。

　　三维人耳模型识别的步骤大致如下：首先使用三维扫描仪获取人侧脸的深度图像；其次将人耳数据从人侧脸数据中准确地提取出来；最后将不同人耳数据或其特征进行配准，通过比较人耳数据之间的配准误差，从而实现三维人耳识别。

1 相关工作

　　迭代最近点（Iterative Closest Points，ICP）算法[1]是目前最常用的三维数据配准算法，通过迭代最小化两待配准点云上对应点间的距离误差，获得最佳的旋转矩阵和平移矩阵，实现精确配准。迭代最近点算法能够满足大多数三维数据的配准要求，但这些算法在不知道待配准模型之间对应点的情况下都需要有一个良好的初始变换，不好的初始变换会导致三维模型局部收敛，直接影响着三维数据的配准效果。因此，为避免该缺陷，许多研究者采用了很多解决方式。2002年Granger等[2]提出EM-ICP算法，将最大期望（EM）算法[3]应用到ICP算法中，从而避免了初始配准的步骤。2005年，Hui等[4]利用两步迭代最近点算法对人耳进行配准，首先利用ICP算法对耳轮数据进行粗配准，然后将该变换矩阵作为初始变换再次应用在ICP算法中，对第一步的匹配进行优化，提高识别效率。2007年，Yan等[5]通过主成分分析（PCA）[6]算法对待配准点云先进行初始配准，调整人耳的姿态，再对初始配准后的结果使用ICP算法进行精确配准。同年，Chen等[7]利用四元组计算初始变换进行粗对齐，再利用ICP算法进行精确匹配。

　　随着三维扫描技术的不断发展，三维扫描仪的扫描精度不断提高，数据规模也随之增大。由于ICP算法、EM-ICP算法均需要对大规模的矩阵进行运算，数据规模的增大必然导致工作效率的降低，传统的串行配准合并算法的效率已无法满足实时性的需求。图形处理单元GPU进行并行计算，由多个流处理器分别进行数值运算，实现任务级和数据级的并行，能够很好地解决上述问题。NVIDIA公司推出的统一计算架构CUDA提供了高性能的GPU并行计算环境，可用于大规模三维数据的处理。由CPU作为主机负责逻辑性强的事务处理和串行计算，GPU作为协处理器完成可并行计算的部分，高度线程化的并行处理任务则由CPU和GPU共同完成，大大提高了程序的运行效率和数据的处理速度，使由于数据规模较大、精度要求较高造成的配准及合并效率降低等问题得以解决。2008年Choi等[8]基于CUDA对ICP算法进行了并行加速，实现了对深度图像进行实时配准。2010年Tamaki等[9]基于CUDA对EM-ICP算法进行了并行加速，配准速度明显提高。

　　根据上述学者们的研究，本文提出了一种两步式迭代最近点算法对三维人耳点云模型进行配准。首先采用基于CUDA加速的EM-ICP算法作为ICP算法的初始配准，使人耳点云数据大致调整为同一姿态，然后基于该算法提供的初始变化采用ICP算法对三维人耳点云数据进行精确配准，相当于进行了两次配准，最终达到配准效果。

2 基于EM-ICP的初始配准

　　初始配准能够有效调整三维模型的位置与姿态，为精确配准提供一个理想的初始变换。本文采用基于CUDA加速的EM-ICP算法对三维人耳模型进行初始变换，EM-ICP算法不需要建立初始对应关系，以权重表示两点间的配准概率，迭代运算优化配准概率，最终实现点云配准。

　　已知三维人耳点云模型X={xi，i=1，…，n}与三维人耳点云模型Y={yi，i=1，…，m}，n与m分别表示人耳点云模型X与Y中点云个数，模型X上的任意一点xi与模型Y上所有点都存在一个对应关系，且用权重的大小来表示配准概率。通过求解模型的变换矩阵R与t，更改人耳点云模型Y的位置，直到点云模型间误差函数E最小。

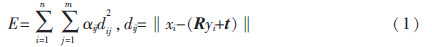
　　其中，ij表示xi与对应点yi的配准概率。

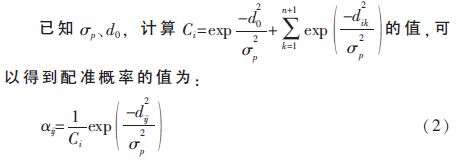
　　因此，点云模型间误差函数E可重写为：

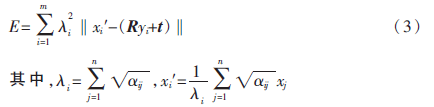
　　EM-ICP算法[2]具体步骤如下：

　　（6）若E大于阈值τ且?滓p小于0.3，则返回到（2），否则迭代结束。

　　EM-ICP算法中，点云模型X上的每一个点都与点云模型Y上所有点存在一个对应关系，即匹配概率ij，因此计算全映射的关系矩阵A=（ij）与两个点云模型的规模密切相关，当点云模型的规模较大时，对矩阵A运算的时间很长，对矩阵A的计算进行GPU并行加速，加快算法效率。

　　对原算法进行并行加速的关键问题是将运算过程分为向量与矩阵的运算和矩阵内元素间的运算两种，利用CUBLAS（CUDA Basic Linear Algebra Subprograms）[10]对向量与矩阵间的运算进行加速，编写CUDA kernel函数对矩阵元素间的运算进行加速[9]。具体步骤如下：

　　（1）将模型X、Y拷贝到显存中，并且对CUDA环境及CUBLAS库函数初始化；

　　（2）计算模型X、Y对应点之间的距离dij；

　　（6）求解旋转矩阵R、平移矩阵t；

　　（7）更新模型Y的位置Y=RY+t；

　　（8）更新控制参数；

　　（9）若E大于阈值τ且p小于0.3，则返回到（2），否则迭代结束。

3 基于ICP的精确配准

　　本文采用ICP算法对粗配准后的三维人耳模型进行精确配准。ICP算法能够对深度图像进行有效的配准，是当前众多配准算法的基础。ICP算法不断地更新一个点云模型的位置，直到该模型与另一个点云模型对应点之间的距离达到某阈值为止。在ICP算法中，点云模型X上的任意一点xi在点云模型Y上有且仅有一个对应点。

　　已知点云模型X={xi，i=1，…，n}与点云模型Y={yi，i=1，…，m}，n与m分别表示人耳点云模型X与Y中点云个数，寻找点云模型X上每一个点xi到点云模型Y上的最近点yi，通过求解模型的变换矩阵R与t，更改模型点云Y的位置，直到点云模型间误差函数E最小。

　　ICP算法的主要目的是求解两个点云模型之间的空间变换，通过这个空间变换使得两点云模型之间的距离最小，其具体步骤如下：

　　（1）点云模型X与模型Y初始对齐；

　　（2）找到点云Y中距离点云X中xi最近的点yi；

　　（3）采用四元数方法解旋转矩阵R，平移矩阵t，并求解；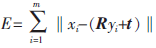

　　（4）更新模型Y的位置X=RX+t；

　　（5）若E大于阈值τ，则返回到（2），否则迭代结束。

4 实验结果及分析

　　实验所用三维扫描仪的分辨率为640×480，帧频为24 f/s。实验程序运行硬件配置为：Intel Xeon E5-2609@2.40 GHz处理器，16 GB内存，NVIDIA Quadro 2000显卡，192个CUDA核心，1 GB GDDR5显存容量，计算能力2.1。系统环境：Fedora 16 Linux，CUDA6.5，GCC4.6.3。

　　4.1 数据采集

　　通过三维激光扫描仪可以得到人耳侧面的扫描数据，但是得到的数据不仅包括人耳数据，还包括人耳附近的皮肤数据，需要将这些无用的数据除去，将人耳数据提取出来。

　　提取到人耳数据后，去掉其颜色信息，得到需要的三维人耳数据模型。在下面的实验中将使用提取得到的三个人耳数据，如图1所示，提取得到的人耳数据，方向各不相同，分别为其编号为ear_a，ear_b，ear_c。

　　4.2 配准效果

　　本文选用CUDA加速的EM-ICP算法作为ICP算法的初始配准，再使用ICP算法进行精确配准。进行两次配准，既保证了配准速度，又保证了配准精度，最终得到了理想的配准效果。如表1所示，将ear_a作为待配准模型，对ear_a与ear_b，ear_a与ear_c分别进行EM-ICP粗配准与ICP精确配准。

　　由表1能够清楚看出，人耳模型ear_b、ear_c经过EM-ICP粗配准后，能够初步调整人耳模型的位置，ICP精确配准后均达到了理想的配准效果。

　　如图2所示，待配准模型ear_a与配准后的ear_b、ear_c模型位置。可以看出，配准后的ear_b、ear_c均调整到与模型ear_a姿态一致的位置。

　　4.3 配准精度

　　将ear_a作为配准模型，对ear_a与ear_b、ear_a与ear_c进行不同方式的配准，如图3所示为分别基于ICP[1]、EM-ICP[9]、两步式ICP[4]以及本文提出的EM-ICP和ICP算法相结合的方式进行配准得到的配准精度。由图可见，本文算法与其他算法相比，具有较高的配准精度，配准效果优于其他方式。

　　4.4 配准时间

　　如表2所示，将分别基于ICP[1]、EM-ICP[9]、两步式ICP[4]以及本文提出的EM-ICP和ICP算法相结合的方式进行配准所用时间进行对比。显然，ICP算法效率略低，EM-ICP算法具有很高的效率，采用两种迭代方式的时间消耗比采用一种迭代方式的时间消耗高，然而在均采用两种迭代方式前提下，本文算法的时间消耗要优于两步式ICP算法，并且本文算法与只基于ICP算法相比，其时间消耗差距不大。

参考文献

　　[1] BESL P J， MCKAY N D. A method for registration of 3-d shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1992，14（2）：239-256.

　　[2] GRANGER S， PENNEC X. Multi-scale EM-ICP： a fast and robust approach for surface registration[C]. Proceedings of the 7th European Conference on Computer Vision. Copen-hagen， Denmark： Springer-Verlag， 2002：418-432.

　　[3] DEMPSTER A， LAIRD N， RUBIN D. Maximum likelihood estimation from incomplete data via EM Algorithm[J]. Journal of the Royal Statistical Society， 1977，39（1）：1-38.

　　[4] CHEN H， BHANU B. Contour matching for 3D ear recognition[C]. In：Proceedings of IEEE Workshop on Application of Computer Vision， 2005：123-128.

　　[5] YAN P， BOWYER K W， Biometric recognition using three-dimensional ear shape[J]. IEEE Trans PAMI， 2007，29（8）：1297-1308.

　　[6] ELAD M， TAL A， AR S. Content based retrieval of VRML objects-an iterative and interactive approach[C]. Proceedings of the Eurographics Workshop in Manchester， United Kingdom， 2001：107-118.

　　[7] CHEN H， BHANU B. Human ear recognition in 3D[J]. IEEE Transaction PAMI， 2007，29（4）：718-737.

　　[8] CHOI S I， PARK S Y， KIM J， et al. Multi-view range image registration using CUDA[C]. Proceedings of the 23rd International Technical Conference on Circuits/Systems， Computers and Communications， 2008：733-736.

　　[9] TAMAKI T， ABE M， RAYTCHEV B， et al. Softassign and EM-ICP on GPU[C]. Proceedings of the 2010 1st International Conference on Networking and Computing， Washington DC， USA： IEEE， 2010：179-183.

　　[10] NVIDIA. CUDA CUBLAS（CUDA Basic Linear Algebra Subprograms）Library[EB/OL].（2015-04-15）. http：//cudazone.nvidia.cn/cublas/.