摘  要： 协同过滤算法是推荐系统中应用最广泛的算法，随着用户数量和物品数量的不断增加，传统的协同过滤算法不能满足推荐系统的实时需求。本文提出了一种融合隐语义模型的聚类协同过滤算法。首先利用隐语义模型分解评分矩阵，然后在分解后的矩阵上利用传统的聚类算法聚合相同类别的物品，最后在相同类别的物品之间进行基于项目的协同过滤推荐。实验结果表明，该算法有效减少了推荐时间，同时在一定程度上提高了算法精度。

　　关键词： 推荐系统；隐语义模型；聚类算法；协同过滤

0 引言

　　随着互联网的蓬勃发展，用户数量和信息量都呈指数型增长。不同的用户都有其个性化的需求，如何快速地在这些复杂环境中找出那些满足用户兴趣的信息，成为亟需要解决的问题。而推荐系统的功能就是针对不同的用户根据其背景和喜好主动推荐信息来满足用户的潜在兴趣[1]。

　　协同过滤技术是现在推荐系统中应用最广的算法[2]，它的主要思想是根据用户对相似项目的评分来预测对目标项目的评分[3-4]。基于这种假设，大部分用户对两个商品i和j的评分都很相似，那么就可以考虑将其中一个商品推荐给只对另一个商品有评分的用户。基于项目的协同过滤找到目标项目的若干近邻，产生推荐列表。传统的协同过滤算法是利用用户的历史行为，来预测用户对目标用户的评分。需要在整个用户空间上去寻找最近邻居。随着电子商务的不断发展，用户数量和物品的数量都呈指数型增长，这样传统的算法就不能够满足推荐的实时需求。同时，传统的协同过滤算法只是考虑了用户的历史行为，而没有考虑物品之间的关系。针对这些问题，本文提出了一种融合隐语义模型的聚类协同过滤算法，区别于传统的基于项目聚类的协同过滤[5]，本文算法没有直接在用户评分矩阵上进行聚类，而是先将评分矩阵进行分解，将得到的矩阵再进行聚类，这样聚类的维度降低，同时还考虑了物品类别信息，提高了推荐系统实时响应速度。

1 相关研究

　　隐语义模型（LFM）是由Simon Funk在Netflix Prize后公布的一个算法[6]。该算法的理论基础是运用SVD矩阵分解，把用户评分矩阵R分解为两个低维矩阵，然后用这两个低维矩阵去估计目标用户对项目的评分。

　　传统的SVD分解需要一个简单的方法补全稀疏矩阵，使矩阵R变成一个稠密矩阵。这种需求在推荐系统面对大数据量的情况时需要很大的存储空间。同时SVD矩阵分解的算法复杂性特别高，在高维稠密数据中进行矩阵分解特别慢。LFM正是为解决这两个问题而提出的。

　　LFM将评分矩阵R分解为两个低维矩阵相乘：

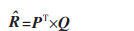
　　其中P∈Rf×m，Q∈Rf×n，而且f<<m，从而达到降维的目的。

　　可以直接通过训练集的观察值，利用最小化RMSE来学习P、Q。损失函数定义为：

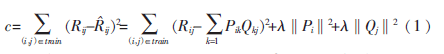
　　其中λ‖Pi‖2+λ‖Qj‖2是用来防止过拟合的正规化项。

　　最小化上面的损失函数可以采用随机梯度下降算法，通过求参数的偏导数来找出最快下降方向，然后迭代地不断去优化参数。

　　首先求出参数的偏导数：

　　然后，根据随机梯度下降算法，得到迭代计算公式：

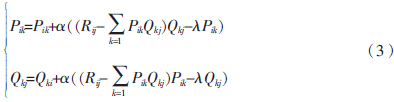
　　当损失函数达到最小值时，迭代结束，得到矩阵P和Q，分别为用户对隐藏类别的兴趣权重和项目属于不同隐藏类别的权重。

2 融合隐语义模型的聚类协同过滤

　　基于项目聚类的协同过滤算法能够有效地降低计算维度，减少运算时间。然而这种算法也存在不足之处。在大型的电子商务系统中，项目的数量很大，例如淘宝上的商品数量多达8亿之多。同时用户的评分项目又很少，一般不会达到1%，所以实际上数据是很稀疏的。直接对这些稀疏的数据进行聚类，效果不是很理想，维度过大。因此提出了融合隐语义模型的聚类算法。

　　2.1 项目聚类

　　传统的协同过滤算法没有考虑物品本身的类别信息，如电影的分类、电商物品的类别等。因此可以利用物品的类别，把相同类别的物品聚类到一块来推荐给喜欢这类物品的用户。但是，实际的推荐系统中物品的数量很大，很难人为地去给物品进行分类，同时有些物品的属性特殊，无法归属于特定的类别。

　　利用LFM可以把用户的评分矩阵R分解为两个矩阵：一个是用户对不同类别物品的喜爱权重矩阵P，另一个是不同物品属于不同类别的权重Q。然后可以在矩阵Q上进行传统的聚类算法[7-8]，把矩阵Q分解为K个簇{C1C2…Ck}，每一个簇就代表一种物品的类别，这样就自动生成了原来很难定义的类别。

　　算法1：融合隐语义模型的聚类算法

　　输入：用户-项目评分矩阵R，聚类个数S

　　输出：S个聚类簇

　　方法：

　　（1）利用公式（1）、（2）、（3）对评分矩阵R进行矩阵分解，得到用户矩阵P和项目矩阵Q：

　　（2）设矩阵Q中项目集合为I={i1，i2…in}；

　　（3）在项目矩阵中任意选择S个项目，作为初始聚类的中心CC={cc1，cc2…ccs}；

　　（4）将S个聚类集合初始化为空，C={c1，c2…cs}；

　　（5）repeat

　　for each item i in I

　　for each item c in CC

　　计算i和c的相似性

　　end for

　　计算i最近的聚类中心，把i加到最近的聚类

　　集合中

　　end for

　　for each item cc in CC

　　计算新的聚类中心

　　end for

　　until聚类中心不变

　　（6）返回。

　　2.2 产生推荐

　　为了得到目标用户的若干邻居，需要度量不同用户的相似性，从而找出与目标用户最相似的邻居集合。相似性度量的方法主要有两种：

　　（1）余弦相似性：采用标准的向量余弦夹角计算，用户Ui和Uj的相似度Sim（Ui，Uj）的计算方法如下：

　　（2）改进的余弦相似性：为了减少不同用户评分尺度上的差异，改进的余弦相似性用减去平均分后的分数计算相似性：

　　在进行协同过滤的最近邻查询时，目标用户的最近邻居大部分分布在与目标项目相似性最高的若干个簇里，因此不需要在整个项目空间上寻找最近邻。算法的复杂度降低。

　　假设目标项目I的最近邻居集合用Ci={Ci1，Ci2…Cik}表示，采用余弦相似度计算相似性，则用户U对项目I的预测评分计算如下：

　　sim（i，j）表示项目i和j之间的相似度，Ri和Rj表示对项目i和j的平均评分。

　　算法2：利用聚类结果产生推荐

　　输入：用户-项目评分矩阵R，项目聚类C，聚类中心CC，邻居个数K，相似度阈值Y。

　　输出：目标用户U对目标项目I的评分。

　　方法：

　　（1）初始化与目标项目I相似的集合SC为空

　　（2）for item cc in CC

　　（3）if sim（cc，i）>Y

　　（4）cc所在的簇加入集合SC

　　（5）end for

　　（6）for item i in SC

　　（7）计算sim（i，I）

　　（8）end for

　　（9）选出相似度最高的k个邻居。

　　（10）利用公式6，计算用户U对目标I的评分。

　　（11）返回。

　　利用算法2可以得到用户对项目的预测评分，从中选出评分最高的K个项目推荐给用户。

　　3 实验结果和分析

　　3.1 数据集及度量标准

　　实验采用MovieLens站点（http：//movielens.umn.edu）提供的数据集[9]。该站点是一个基于Web的研究性推荐系统，用于接受用户对电影的评分并且提供相应的推荐列表，该数据集包含943个用户对1 682部电影的100 000个评分，评分的范围为1~5，而且每个用户至少有20个评分。整个实验根据需要进一步划分数据集，其中的80%作为训练集，20%作为测试集。

　　实验采用绝对偏差MAE作为度量标准，通过计算预测评分与实际评分之间的差别来度量算法的准确性，MAE越小，算法的准确性越高。设通过算法预测的评分为，用户实际的评分为{P1，P2…Pk}，则MAE的定义为：

　　3.2 实验结果与分析

　　本文提出的算法并不保证能够找到目标项目的所有最近邻，因为聚类形成的簇中心可能远离目标项目。下面把所提出改进算法与基于项目的协同过滤进行比较，使用MAE和运行时间作为度量标准。

　　固定邻居个数k=20，可以得到不同聚类个数对MAE的影响，如图1所示。

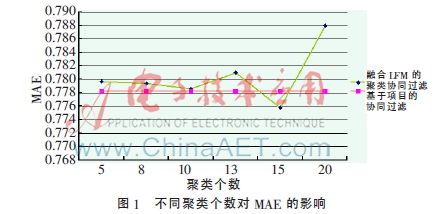
　　如图1所示，当k=15时，本文提出的算法的MAE达到最小值，比基于项目的协同过滤还要小，但随着聚类个数的增加，MAE开始变大。

　　固定聚类个数c=10，可以得到不同邻居个数对算法MAE的影响，如图2所示。

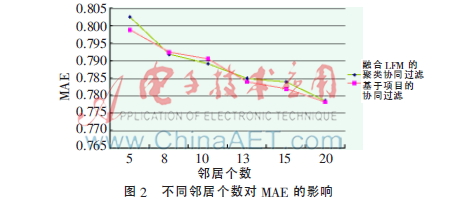
　　如图2所示，算法在不同邻居个数上的MAE与Item-Base保持基本相同，在某些邻居点上算法的MAE更小。

　　固定邻居个数k=20，可以得到不同聚类个数产生推荐的时间，如图3所示。

　　如图3所示，融合LFM的聚类协同过滤算法的运行时间远远小于传统的协同过滤算法，能够更好地满足推荐的实时要求。

4 结论

　　针对传统的基于项目的协同过滤算法在面对大数据量的情况下表现出的性能不佳，以及基于项目聚类算法不能很好地应对稀疏数据、没有考虑物品类别等问题，本文提出了一种融合隐语义模型的聚类协同过滤算法。算法首先对用户的评分数据进行矩阵分解，得到物品的类别信息；然后在分解后的矩阵上进行传统的聚类算法。实验表明，本文提出的算法可以有效提高推荐系统的响应速度。同时由于利用了隐语义模型，推荐的过程中加入了商品类别信息，从而在一定程度上提高了算法的精度。

参考文献

　　[1] SCHAFER J B， KONGSTAN J A， RIED J. E-commerce recommendation applications[J]. Data Mining and Knowledge Discovery， 2001，5（1/2）：115-153.

　　[2] 王国霞，刘贺平.个性化推荐系统综述[J].计算机工程与应用，2012，48（7）：66-76.

　　[3] SARWAR B， KARYPIS G， KONSTAN J， et al. Item-based collaborative filtering recommendation algorithms[C]. In Proceedings of the Tenth International World Wide Web Conference， 2001：285-295.

　　[4] DESHPANDE M， KARYPIS G. Item-based top-N recommendation algorithms[J]. ACM Transactions on Information Systems， 2004，22（1）：143-177.

　　[5] 邓爱林，左子叶，朱杨勇.基于项目聚类的协同过滤推荐算法[J].小型微型计算机，2004，25（9）：1665-1670.

　　[6] DUMAIS S T. Latent semantic analysis[J]. Annual Review of Information Science and Technology， 2004，38（1）：188-230.

　　[7] DEMPSTER A， LAIRD N， RUBIN D. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society， 1977，38（1）：1-38.

　　[8] THIESSON B， MEEK C， CHICKERING D， et al. Learning mixture of DAG models[C]. Proceeding of the Fourteenth Conference on Uncertainty in Articial Intelligence， 1998：504-513.

　　[9] MILLER B N， ALBERT I， LAM S K， et al. Movie lens unplugged： experiences with an occasionally connected recommender system[C]. Proceedings of the 8th International Conference on Intelligent User Interfaces， New York， 2003： 263-266.