摘  要： 联合相容分支定界算法（Joint Compatibility Branch and Bound，JCBB）充分考虑传感器量测之间的相关性和重新匹配关联的可能，但计算量随观测数目成指数增长。为优化其计算复杂度和关联准确度，以最近邻算法（Nearest Neighbour，NN）进行关联，对符合重复度和经过设定步数的情况使用JCBB进行特征匹配，并以互斥准则和最优准则来提高关联准确度。引入机器学习领域的评价测度对改进后算法和JCBB算法进行比较，结果表明，改进后的关联算法能够保证更好的关联准确度。

　　关键词： 联合相容分支定界算法（JCBB）；数据关联；特征匹配；准确度

0 引言

　　数据关联源于目标跟踪领域，用于确定传感器量测信息和目标源之间的对应关系，错误的数据关联不仅影响导航和定位精度，甚至会导致整个关联算法不一致或者发散[1]。

　　Singer等人提出的最近邻（Nearest Neighbor，NN）[2]算法是最早也是最简单的数据关联方法，当观测量和特征之间的统计距离度量最小或者残差概率密度最大时认为两者可以关联，在环境特征密度较大的情况下，容易发生关联失败现象。Bar-Shallom和Jaffer提出的概率数据关联（Probability Data Association，PDA）算法充分利用过去一定时间内的数据信息，不依赖于过去数据关联的正确性，提高了算法的收敛性，但对计算开销要求有所提高。对PDA改进后的联合概率数据关联（Joint Probability Data Association，JPDA）[3]算法对所有可能的关联假设集合进行搜索，并以此为基础寻找最优关联。针对NN算法忽略环境特征之间相关性的问题，Jose Neira 等人提出了联合相容性检验（Joint Compatibility test，JC test）算法，检验一次观测获得的所有观测和地图特征之间的联合相容性，联合相容分支定界（Joint Compatibility Branch and Bound，JCBB）[4]算法能排除一些NN无法排除的关联假设，结合分支定界法和相容性的递增式计算搜索解释树的方法来获得最优解。数据关联方法还有多假设数据关联[5]、基于图论的关联算法[6]、惰性数据关联[7]、基于信息理论关联[8]等，它们都寻求在计算复杂度和关联准确度之间获得更好效果，在目标跟踪、数据融合等领域[9-11]都有广泛涉及。

　　在保证计算复杂度不增加的前提下，考虑算法计算复杂度和准确度两要素，将最近邻算法与联合相容分支定界算法结合使用，并以互斥准则、最优准则约束误关联情况，从而提高关联准确度，降低错误关联导致整个算法发散的可能，进而保证定位和更新精度。

1 问题定义

　　1.1 特征关联

　　移动机器人在导航过程中需要构建环境地图并且确定自身在地图中的位姿，数据关联是机器人在观测到环境特征之后对观测量进行分类应用或整合的过程，用以确定当前的一个或者多个观测量是否应该对应到地图中的已有特征以及对应到哪一个特征。

　　图1中三角形表示移动机器人，其顶点作为传感器所在位置，以圆形表示机器人构建地图中已有的特征点，记为F1~F5，以方形表示当前传感器的观测量z1~z5，椭圆表示以某种距离度量表示的地图特征的匹配范围，忽略传感器所得观测量是虚警信息的情况。z1和z2分别落在F1和F2的可匹配范围之内，两对观测—特征对可以进行匹配；对于z3和F3以及z3和F5均可视为匹配对，若仅以直观距离最近原则选择会舍去其与F5的匹配，因其与F3距离更近；观测量z4未落在任一特征的匹配范围内，将其视作待加入地图的新特征F6。对所有观测量和特征点进行匹配即完成了数据关联过程，如图1右图所示的关联结果直接影响地图创建中特征位置的更新，以及新特征的加入，进而影响机器人自身定位过程。

　　1.2 马氏距离与卡方检验

　　马氏距离（Mahalanobis Distance）表示数据协方差之间的距离，是计算两个未知样本集之间相似程度的有效方法。其与欧氏距离的不同在于它考虑不同特征之间的相关性且与测量尺度无关。对均值为、协方差为的N维观测量z，其马氏距离的平方为：

　　利用Cholesky分解=CCT替换变量，则以变量y=C-1（z-），得：

　　由此得马氏距离的平方服从自由度为N的卡方分布。以符合不同自由度和准确度要求的卡方分布检验两个样本集之间是否足够相似，这种方法在关联问题中得到广泛应用。

2 算法

　　2.1 联合相容分支定界算法

　　JCBB算法的核心是联合相容准则，用以检验所有观测值与地图特征点之间的相容性。相容性检验标准也采用马氏距离，由于同时考虑所有特征与机器人之间的相关性，其匹配准确度高于最近邻算法。对于一次关联对应假设集为Hk={j1，j2，…，jk}时，扩展卡尔曼滤波过程中的联合观测方程表示为：

　　在当前估计状态处的线性化过程为：

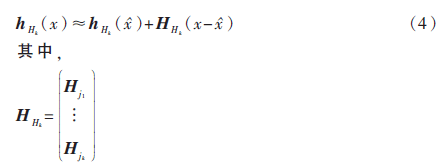
　　联合信息及其协方差为：

　　联合相容检测准则为：

　　其中，ｄ是联合观测量的维数，是要求的置信度。如果马氏距离满足式（7），则认为关联解Hk满足联合相容条件。然后对关联解空间采用分支定界方法进行遍历，以配对数目单调非减规则为定界条件，以联合相容条件为分支准则，搜索并最终决定观测值和地图特征点之间的最佳关联解。

　　2.2 改进算法

　　初始使用最近邻算法对多个观测值进行数据关联，若无多个观测值对应同一个特征的情况，则接受所得关联结果。若出现干涉现象则调用联合相容分支定界算法完成关联。若在JCBB关联过程中仍出现干涉现象，则以一次关联中仅允许一个地图特征与一个观测量完成关联，若再有此特征关联则被拒绝，避免多观测量对同一地图特征的重复匹配。

　　搜索解空间过程若有多个符合最大匹配数目的关联解，最优准则选定为：选择其中Mahalanobis距离最小的关联解作为关联结果。

　　改进算法针对关于计算复杂度的考虑，结合NN计算复杂度低的特点，并以相应准则解决JCBB可能存在的干涉现象和存在多个可能的最优解的情况以保证关联准确性。

3 实验

　　3.1 评定指标

　　引入机器学习中的评价测度对关联性能进行评定。以真/假（true/false）说明判断正误，以正/负（positive/negative）表示判定结果，正例判定为正例称为真正（true positive，TP），负例判定为负例称为真负（true negative，TN），正例判定为负例称为假负（false negative，FN），负例判定为正例称为假正（false positive，FP）。准确率（Accuracy）反映关联算法的整体判定能力（能将正例判定为正例，负例判定为负例），精确度（Precision）反映判定的正例中真正的正例样本的比重，召回率（Recall）反映被正确判定的正例占总的正例的比重。用Precision和Recall评估一种算法，当两者均更高时，才能说明分类算法的性能更优于另一种算法。然而事实上两者在某些情况下是矛盾的，采用评价测度F Score（F Measure）可以综合考虑精确度和召回率，它是二者的加权调和平均。Accuracy（记为A）、Precision（记为P）、Recall（记为R）、F Score（记为F），依次定义为：

　　A=（TP+TN）/（TP+TN+FP+FN）（8）

　　P=TP/（TP+FP）（9）

　　R=TP/（TP+FN）（10）

　　F=（（a2+1）P×R）/（a2P+R）（11）

　　特别地，当参数a=1时，成为最常见的F1 Score（F1 Measure）测度，即

　　F1=2P×R/（P+R）（12）

　　3.2 实验参数设置

　　仿真实验设置为机器人从世界坐标（0，0）出发，在规模为180 m×250 m的环境中，沿规定路径运动，依据激光测距仪传回的观测信息，对环境中的62个特征点进行定位，并最终返回起始点。仿真参数设置如下：将生成随机噪声的种子设置为23，运动噪声和观测噪声的方差分别设定为：ν=0.7 m/s，?酌=3°；ρ=0.3 m，b=4°。机器人运动速度为4 m/s，最大转向角速度为±20°/s，最大转向角±30°，激光最大扫描距离30 m，扫描范围0°~180°，控制周期和观测周期均为0.1 s，前后轮间距为4 m。

　　3.3 实验结果分析

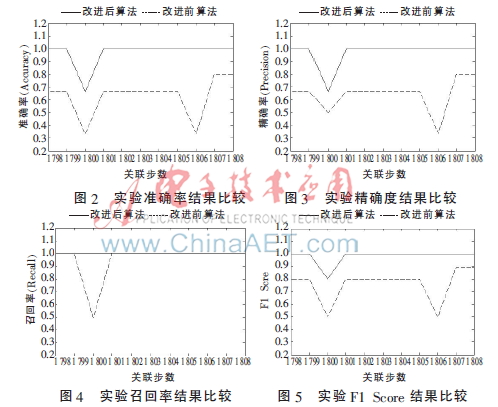
　　通过图2~图5针对不同指标比较结果可知，当改进前关联算法的准确率和精确度变低时，改进后算法的准确率和精确度仍保持较高；以召回率和精确度都较高或者以综合了精确度和召回率的F1 Score作为评价原则，改进后算法关联性能都优于改进前。调整噪声参数，改进后算法仍能保持更优的关联性能。

4 结束语

　　针对联合相容分支定界算法计算复杂度较高的缺点，为改进其关联性能，考虑最近邻算法计算复杂度低及可能出现的干涉现象和搜索最优解可能出现的匹配数相同的情况，将其与最近邻算法和最优及互斥准则融合，改进算法提高了关联准确度，降低了错误关联引起算法发散的概率，进而减少机器人对自身位姿和构图的不确定性。在更复杂环境下的关联方法选择和计算复杂度处理是待研究的问题。

参考文献

　　[1] DURRANT-WHYTE H， BAILEY T. Simultaneous localization and mapping： part I[J]. Robotics & Automation Magazine， IEEE， 2006，13（2）：99-110.

　　[2] BEIS J S， LOWE D G. Shape indexing using approximate nearest-neighbour search in high-dimensional spaces[C]. Proceedings of the IEEE 1997 Computer Society Conference on Computer Vision and Pattern Recognition， 1997：1000-1006.

　　[3] FORTMANN T E， BAR-SHALOM Y， SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J]. Oceanic Engineering， IEEE Journal of， 1983，8（3）： 173-184.

　　[4] NEIRA J， TARD?魷S J D. Data association in stochastic mapping using the joint compatibility test[J]. Robotics and Automation， IEEE Transactions on， 2001，17（6）：890-897.

　　[5] COX I J， LEONARD J J. Modeling a dynamic environment using a Bayesian multiple hypothesis approach[J]. Artificial Intelligence， 1994，66（2）：311-344.

　　[6] BAILEY T， NEBOT E M， ROSENBLATT J， et al. Data association for mobile robot navigation： a graph theoretic approach[C]. Robotics and Automation， 2000. Proceedings. ICRA′00. IEEE International Conference on. 2000：2512-2517.

　　[7] H?魧HNEL D， THRUN S， WEGBREIT B， et al. Towards lazy data association in SLAM[C]. Robotics Research. 2005， Springer： 421-431.

　　[8] KAESS M， DELLAERT F. Covariance recovery from a square root information matrix for data association[J]. Robotics and Autonomous Systems， 2009，57（12）：1198-1210.

　　[9] CHONG C Y， KUMAR S P. Sensor networks： evolution， opportunities， and challenges[J]. Proceedings of the IEEE， 2003， 91（8）： 1247-1256.

　　[10] DALLIL A， OUSSALAH M， OULDALI A. Sensor fusion and target tracking using evidential data association[J]. Sensors Journal， IEEE， 2013，13（1）：285-293.

　　[11] WU Z， THANGALI A， SCLAROFF S， et al. Coupling detection and data association for multiple object tracking[C]. Computer Vision and Pattern Recognition （CVPR）， 2012 IEEE Conference on. 2012： 1948-1955.