摘  要： 提出基于脑电信号（EEG）的睡眠分期研究。利用离散小波变换（DWT）的db8小波分解得到的细节分量作为信号新的表达，把各个细节分量能量作为特征，建立带高斯径向基核函数（RBF）的非线性支持向量机（SVM）模型。研究发现，其对睡眠分期研究的方案是可行的，满足模型对泛化能力的要求。

　　关键词： 睡眠分期；离散小波变换；支持向量机

0 引言

　　睡眠是人体一种非常重要且不可或缺的生理活动，但工作压力、疾病、不良的生活习惯等因素会影响人的睡眠质量，长期睡眠质量低下会引发各种心理、生理疾病。依据生理信号数据自动识别睡眠，分期对睡眠状态与睡眠质量的科学评估以及相关疾病的诊断及治疗有很重要的意义和参考价值。

　　对睡眠的研究往往是基于相关生理数据。在清醒和不同睡眠阶段，人的脑电信号（Electroencephalogram，EEG）在不同的脑区会出现不同的节律变化分布，可以表征人体的不同睡眠阶段。参考文献[1-3]提取最小值、最大值、均值、标准差等频域特征和排列组合熵、样本熵等非线性动力学参数，但其样本较少，模型推广性能不足。参考文献[4]分别使用Choi–Williams分布、连续小波变换和Hilbert-Huang变换（Hilbert-Huang Transform，HHT）提取特征，利用随机森林分类器说明不同方法提取特征对分类器的准确率有一定影响，其中使用CWT提取特征的分类器准确率最高。参考文献[5-6]分别建立复发性神经分类器和支持向量机（Support Vector Machine，SVM）模型，对非快速眼动深睡期没有细分。而参考文献[7]使用EEG各个节律波频带的相对功率作为特征，所建立的SVM模型准确率高于神经网络（Neural Network，NN）模型，该研究只是将睡眠分为4个阶段，未具体区分非快速眼动睡眠各个阶段，且清醒期的识别率偏低，并没有突出提高清醒期识别率的基础作用。参考文献[8]研究了25位受试者睡眠EEG、眼电（Electrooculogram，EOG）和肌电（Electromyogram，EMG）信号，提取特征后在深度信念网络（Deep Belief Networks，DBN）基础上建立的马尔科夫模型准确率高于未提取特征的模型准确率，说明提取特征是建立模型的重要步骤。由于样本来自疑似睡眠呼吸障碍者，该模型具有较强的针对性和局限性。

　　由于人的生理信号存在个体差异，当被试者人数增加时与信号特征离散性增大，而导致模型的推广能力下降。本文使用Sleep-EDF数据库EEG Fpz-Cz、EEG Pz-Oz这2个通道的数据。采样频率为100 Hz，由专家根据R&K标准[9]，基于经验标定受试者每30 s区间的状态。R&K标准将睡眠分为6个阶段，分别是清醒期（Wake）、非快速眼动期（Non-Rapid Eye Movement，NREM）和快速眼动期（Rapid Eye Movement，REM），其中NREM又可分为浅睡期（包括NREM1、NREM2）和深睡期（包括NREM3、NREM4）。

1 离散小波变换

　　利用EEG将睡眠分期的关键是对能表征各个睡眠阶段的特征进行提取。受试者在长时间的测试过程中，电极松动或移动会带来基线漂移，而对频谱图的研究发现，低频信号的幅值相对较大，尤其以1 Hz以内的幅值最为显著，据此可以判断，信号主要存在基线漂移现象。通过离散小波变换处理数据，在消除基线漂移之后提取各个分量的能量作为模型特征。

　　小波变换是在傅里叶变换的基础上发展起来的一种时频分析方法，在处理非平稳信号方面，具有良好的时频特性。由于实验采集到的信号大多是经过采集系统采集的离散数据，因此离散小波变换的应用非常广泛[10]。将信号f（t）进行k尺度离散小波变换，计算公式如下：

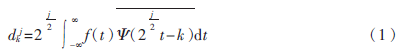
　　原始时域信号经由离散小波变换得到逼近分量   Ai（t）和细节分量Di（t）（i=1，2，...，k）。本文使用db8小波分解，分别得到细节分量Di（t）（i=1，2，...，8）和逼近分量A8（t）。细节分量Di（t）（i=1，2，...，8）从D1（t）到 D8（t）的频率逐次降低。其中，D7（t）和D8（t）的频谱主要集中在1 Hz以内，故可以将其作为基线漂移分量，置零即可。图1显示了一名受试者在REM期的EEG Fpz-Cz通道的30 s信号经离散小波变换得到细节分量Di（t）（i=1，2，…，6）的频域信号。

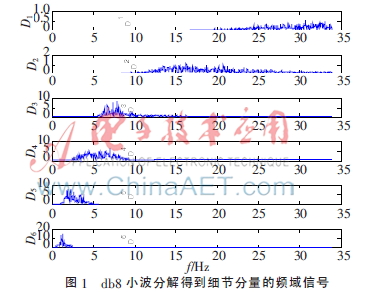
　　在不同睡眠阶段，各个细节分量的能量不同，可以作为特征区分各个睡眠阶段。本文使用细节分量Di（t）（i=1，2，...，6）的能量信息作为部分特征实现睡眠分期。

2 非线性SVM模型分析

　　SVM在解决小样本、非线性及高维模式识别中表现出许多特有的优势。非线性SVM问题的基本思想是，通过非线性变换，将输入变量x转化到某个高维空间，然后再变换空间求最优分类面。非线性SVM问题的最优化目标是：

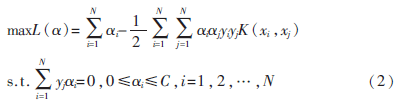
　　相应的判决函数为：

　　如果y≥0，判为一类，类别为1；否则，类别为-1。

　　式（2）和式（3）中K（xi，x）为核函数，本文选择使用了高斯径向基核函数：

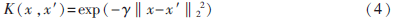
　　参数C、选择对模型的准确性有很大的影响，本文使用了基于交叉验证的网格搜索法来进行SVM参数寻优。

3 实验结果

　　选取Sleep-EDF数据库中8位受试者的数据。将6位受试者的数据作为一组，其中的75%用来建立非线性SVM模型，剩余的25%用来测试模型精度，验证模型是否出现过拟合问题。利用额外2位受试者的数据测试模型的精度，验证模型的泛化能力。本研究的整体流程如图2所示。

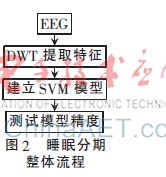
　　使用台湾林智仁的LIBSVM作为研究平台。模型测试精度如表1所示。

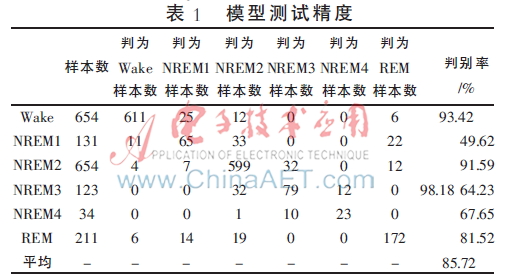
　　本文模型的分期平均准确率为85.72%，说明模型没有出现过拟合。实际有以下方面对模型精度存在较大的影响：原始时域EEG信号中的干扰成分过多；专家标定状态本身就有一定误差；睡眠的各个阶段是连续的；等等。

　　使用已经建立的SVM模型，将剩余2名受试者的数据经测试对比，平均精度为81.65%。因此，本文的模型满足了对泛化能力的要求，验证了本研究的可行性。

4 结论

　　使用脑电信号研究睡眠分期对数据预处理、降维处理、提取特征、分类器的选择都是很重要的环节。本文对db8小波分解EEG得到的各个层次小波提取能量特征，使用SVM进行睡眠分期。本文的模型经过测试之后，达到比较理想的分类效果，即具有良好的推广能力。

　　本文的研究只是基于EEG。在今后的研究中，还有很多工作需要进一步深入研究，也可将其他的生理指标引入睡眠分期的研究，如EOG、心电（Electrocardiogram，ECG）、EMG，相信也会有好的研究前景。

参考文献

　　[1] GNE?S， POLAT K， YOSUNKAYA . Efficient sleep stage recognition system based on EEG signal using K-means clustering based feature weighting[J]. Expert Systems with Applications， 2010，37（12）：7922-7928.

　　[2] 李谷，范影乐，庞全.基于排列组合熵的脑电信号睡眠分期研究[J].生物医学工程学杂志，2009，26（4）：869-872.

　　[3] 周鹏，李向新，张翼，等.基于主成分分析和支持向量机的睡眠分期研究[J].生物医学工程学杂志，2013，30（6）：1176-1179.

　　[4] FRAIWAN L， LWEESY K， KHASAWNEH N， et al. Automated sleep stage identification system based on time–frequency analysis of a single EEG channel and random forest classifier[J]. Computer Methods and Programs in Biomedicine， 2012，108（1）：10-19.

　　[5] HSU Y L， YANG Y T， WANG J S， et al. Automatic sleep stage recurrent neural classifier using energy features of EEG signals[J]. Neurocomputing， 2013，104：105-114.

　　[6] KOLEY B， DEY D. An ensemble system for automatic sleep stage classification using single channel EEG signal[J]. Computers in Biology and Medicine， 2012，42（12）：1186-1195.

　　[7] LEE J， YOO S K. Electroencephalography analysis using neural network and support vector machine during sleep[J]. Engineering， 2013（5）：88-92.

　　[8] L?魧NGKVIST M， KARLSSON L， LOUTFI A. Sleep stage classification using unsupervised feature learning[J]. Advances in Artificial Neural Systems， 2012，2012：9.

　　[9] RECHTSCHAFFEN A， KALES A. A manual of standardized terminology， techniques and scoring systems for sleep stages of human subjects[M]. Los Angeles： UCLA Brain Information Service/Brain Research Institute， 1968.

　　[10] OCAK H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy[J]. Expert Systems with Applications， 2009， 36（2）： 2027-2036.