摘 要: 以固高GRB-400机器人和摄像机组成手眼系统,在手眼关系旋转矩阵的标定方面,分析了基于主动视觉的标定方法。为实现手眼关系平移向量的标定,提出以固定于机械臂末端的激光笔来获取工件平台上特征点的基坐标,并结合已标定的旋转矩阵来标定平移向量。最后,从图像求取多个特征点之间的距离并与实际值进行误差比较,平面特征点间的长度测量误差在±0.8 mm之间,表明手眼标定精度较高,可满足机器人进行工件定位与自动抓取的要求。
关键词: 机器人;手眼系统;主动视觉;激光笔;标定
0 引言
当今,机器人视觉系统以其精度高、成本效率高、连续性、灵活性等特点被广泛应用于电子原件装配、焊接工程、零配件尺寸检查等领域。手眼标定是机器视觉系统中的关键技术,手眼标定的精度将直接影响系统的定位精度。因此,为提高系统的定位精度,需要大量的实验来实现手眼标定,以减小最终误差。在手眼标定方面许多学者做了努力,并取得了一定的成果,如Ma[1]提出了主动视觉的方法,通过摄像机的正交平移运动,利用极点建立约束方程组,求解摄像机内参数及手眼关系;杨广林[2]等给出一种手眼标定方法,仅需场景中的两个特征点,通过控制摄像机做两次平移运动和一次旋转运动即可实现手眼标定。此外,针对一些机器人如SCARA机器人,其在做旋转运动时仅能绕z轴旋转,对于一些手眼标定方法该类机器人无法实现,如Shiu[3]和Tsai[4]的手眼标定方法均要求至少需要旋转轴不平行的两组运动,才能唯一确定手眼矩阵的各分量。本文以固高GRB-400机器人和摄像机组成的手眼系统为研究对象,采用基于主动视觉的手眼标定方法对手眼关系的旋转矩阵进行标定,借助于激光笔来获取工件平台上特征点的世界坐标,然后根据特征点的世界坐标和已标定的旋转矩阵来求取手眼关系的平移向量。
1 固高GRB-400机器人
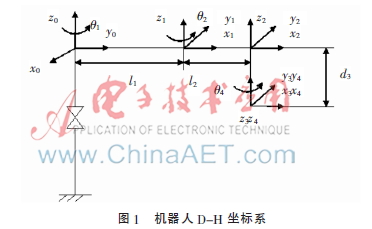
四自由度GRB-400机器人是典型的SCARA机器人,具有3个旋转关节和1个移动关节,采用D-H法建立坐标系,如图1所示。从控制器中获取关节变量?兹1、?兹2、?兹4、d3,由图1可求得各连杆的变换矩阵,从而得到机械臂末端的位姿参数:

其中,![9`NN$K1]EL{]O0IGN{JS)~9.jpg 9`NN$K1]EL{]O0IGN{JS)~9.jpg](http://files.chinaaet.com/images/2016/02/17/6359133448810192572187639.jpg) 分别表示基坐标系与机械臂末端坐标系之间的旋转矩阵和平移向量。
分别表示基坐标系与机械臂末端坐标系之间的旋转矩阵和平移向量。
易知其中的旋转矩阵 具有如下形式:
具有如下形式:

2 手眼关系的标定
2.1 手眼系统中的坐标变换
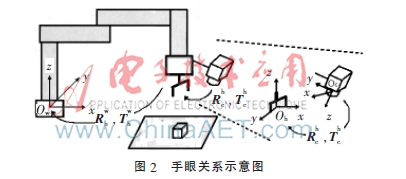
手眼关系示意图如图2所示,Qw-xyz、Qh-xyz和Qc-xyz分别表示机器人基坐标系、机械臂末端坐标系和摄像机坐标系,![9`NN$K1]EL{]O0IGN{JS)~9.jpg 9`NN$K1]EL{]O0IGN{JS)~9.jpg](http://files.chinaaet.com/images/2016/02/17/6359133453422792576505331.jpg) 分别表示基坐标系与机械臂末端坐标系之间的旋转矩阵和平移向量,Rhc和Thc分别表示机械臂末端坐标系与摄像机坐标系之间的旋转矩阵和平移向量。设P为空间中的一点,Pw、Ph和Pc分别为点P在坐标系Qw-xyz、Qh-xyz和Qc-xyz中的坐标,则P在手眼系统中各坐标系之间的关系如下:
分别表示基坐标系与机械臂末端坐标系之间的旋转矩阵和平移向量,Rhc和Thc分别表示机械臂末端坐标系与摄像机坐标系之间的旋转矩阵和平移向量。设P为空间中的一点,Pw、Ph和Pc分别为点P在坐标系Qw-xyz、Qh-xyz和Qc-xyz中的坐标,则P在手眼系统中各坐标系之间的关系如下:

2.2 手眼关系中旋转矩阵的标定
在手眼系统中,当控制机械手做平移运动时,摄像机也随着机械手做平移运动。参考文献[1]给出了确定摄像机坐标系平移方向的方法。
当控制机械手做一次平移运动时,设其平移向量为 k 1,相应的摄像机平移向量为k
1,相应的摄像机平移向量为k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133468414492574657021.jpg) 1(
1(![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133468875092576468684.jpg) 1、
1、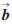 1均为单位向量),设P点在机械臂坐标系平移前后的坐标分别为Ph和Ph+k
1均为单位向量),设P点在机械臂坐标系平移前后的坐标分别为Ph和Ph+k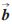 1,在摄像机坐标系平移前后的坐标分别为Pc和Pc+k
1,在摄像机坐标系平移前后的坐标分别为Pc和Pc+k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133472592192577918179.jpg) 1,根据式(3)可得:
1,根据式(3)可得:
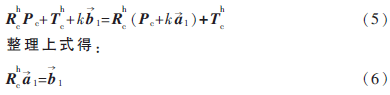
类似地,控制机械手沿不同方向做两次平移运动,设其平移向量分别为k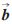 2、k
2、k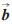 3,相应的摄像机平移向量分别为k
3,相应的摄像机平移向量分别为k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133475870992576554478.jpg) 2、k
2、k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133476400892572820030.jpg) 3(
3(![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133476866292573846847.jpg) i、
i、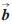 i均为单位向量,i=2,3),同样可推得:
i均为单位向量,i=2,3),同样可推得:

将式(6)~(8)合成矩阵形式有:
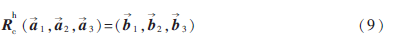
由此可得手眼关系的旋转矩阵:
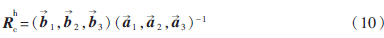
在实际标定过程中,可以只通过控制机械手沿相互正交的两个方向平移,然后采用施密特正交化方法对得到的两个摄像机平移向量进行正交化,第三个平移向量![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133480238492573866574.jpg) 3、
3、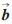 3由前两项叉乘得出,即
3由前两项叉乘得出,即![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133481283892575898447.jpg) 3=
3=![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133481916992573046662.jpg) 1×
1×![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133482439192574798890.jpg) 2,
2,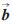 3=
3=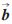 1×
1×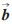 2,由此可求得正交的旋转矩阵
2,由此可求得正交的旋转矩阵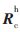 。
。
2.3 手眼关系中平移向量的标定
手眼关系的平移向量是通过以固定于机械臂末端的激光笔来获取工件平台上特征点的基坐标,并结合已标定的旋转矩阵来标定的。
2.3.1 基于激光笔求工件平台上特征点的基坐标
基于激光笔求特征点基坐标的示意图如图3所示,工件平台与基坐标的z轴垂直(设工件平台在z轴的坐标位置已知),P为工件平台上位置固定的特征点,设其基坐标表示为(wxp,wyp,wzp)T,激光笔安装于机械臂末端,即Qh-xyz坐标系的A处,且使激光射线平行于Qh-xyz的z轴。可通过控制机械手上下移动观察激光射线是否打在工件平台上的同一点来判断激光射线是否平行于Qh-xyz的z轴,若不是则调整激光笔直到激光射线与Qh-xyz的z轴相平行。易知当激光射线与Qh-xyz的z轴相互平行时,激光射线上的点在Qh-xyz上具有相同的x、y轴坐标值且不随机械手的移动而改变,设分别为hxp、hyp。
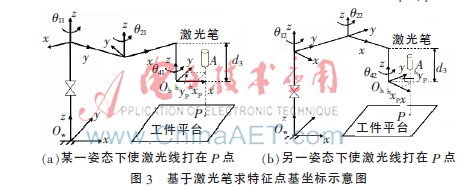
首先,通过调整机器人的四个关节状态使激光射线打在P点上(如图3(a)所示),设此时P点在Qh-xyz中的坐标为(wxp,wyp,wzp)T,从控制器中获取当前机器人的关节变量分别为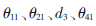 ,根据D-H法可求得机械臂末端的位姿参数
,根据D-H法可求得机械臂末端的位姿参数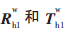 ,易知旋转矩阵
,易知旋转矩阵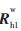 具有如式(2)的形式,设为:
具有如式(2)的形式,设为:

接着,保持机械臂末端与工件平台的距离不变,即机器人的移动关节参数值仍为d3,改变机器人的其他三个旋转关节,且仍使激光射线打在P点上(如图3(b)所示),显然此时的P点在Qh-xyz中的坐标仍为(wxp,wyp,wzp)T,从控制器中获取当前机器人的关节变量分别为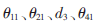 ,同理可求得
,同理可求得 ,且旋转矩阵
,且旋转矩阵![7N@K(%449G(R}QG}ZJ3~]0U.png 7N@K(%449G(R}QG}ZJ3~]0U.png](http://files.chinaaet.com/images/2016/02/17/6359133512604692571708812.png) 具有式(2)的形式:
具有式(2)的形式:

由式(12)、(13)可解得:
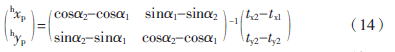
在基坐标系下,对于工件平台上的特征点的z轴坐标值相等且为已知,因此只需求取x、y轴的坐标值。将求得的(hxp,hyp)T带入式(12)即可求得P点在基坐标系下的x、y轴的坐标值。为减小(hxp,hyp)T的误差,可采用对不同特征点重复多次实验求平均的方法。
2.3.2 平移向量的标定
根据手眼系统中的坐标变换关系,由式(3)、(4)可得:

标定过程:控制机械手使工件平台上已知基坐标的特征点置于场景中,从控制器中获取当前机器人的关节变量求得![9`NN$K1]EL{]O0IGN{JS)~9.jpg 9`NN$K1]EL{]O0IGN{JS)~9.jpg](http://files.chinaaet.com/images/2016/02/17/6359133518247392575045818.jpg) ,从图像上获取特征点的图像像素坐标(u,v),zc可由参考文献[2]给出的方法求得,
,从图像上获取特征点的图像像素坐标(u,v),zc可由参考文献[2]给出的方法求得,![6])K%3AGN@_4W]`7H)ZL)QN.jpg 6])K%3AGN@_4W]`7H)ZL)QN.jpg](http://files.chinaaet.com/images/2016/02/17/6359133522570392577186571.jpg) 、M均已标定求出,则由式(19)即可求得手眼关系的平移向量
、M均已标定求出,则由式(19)即可求得手眼关系的平移向量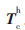 。通过重复多次实验求平均,可减少误差。
。通过重复多次实验求平均,可减少误差。
3 实验结果及分析
本文的手眼系统的硬件部分主要有:四自由度GRB-400机器人、机器人控制柜、控制计算机、CCD摄像头、图像采集卡及其他辅助设备。摄像机安置于机械臂手爪的旋转关节上,其采集的图像尺寸为2 048× 1 536。
3.1 手眼关系旋转矩阵的标定实验
控制机械手沿机械臂末端坐标系的Zh+(“+”表示坐标轴的正方向,“-”表示坐标轴的负方向)方向移动 10 mm,根据移动前后图像特征对应点求取摄像机的平移向量k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133525739092572899464.jpg) 1,再控制机械手沿机械臂末端坐标系的Yh+方向移动10 mm,同样可求得摄像机的平移向量k
1,再控制机械手沿机械臂末端坐标系的Yh+方向移动10 mm,同样可求得摄像机的平移向量k![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133526376792573561005.jpg) 2,利用Schmidt正交化,令
2,利用Schmidt正交化,令![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133527300392574642821.jpg) 3=
3=![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133528446392575800694.jpg) 1×
1×![KMTASD)]WSY$MQ6V]FEHJSP.jpg KMTASD)]WSY$MQ6V]FEHJSP.jpg](http://files.chinaaet.com/images/2016/02/17/6359133529153192575617952.jpg) 2,同时利用机械手平移的方向向量由式(10)求得手眼关系的旋转矩阵
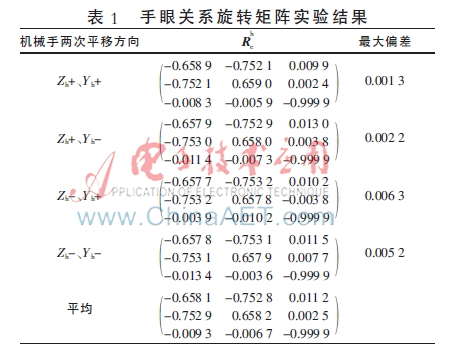
2,同时利用机械手平移的方向向量由式(10)求得手眼关系的旋转矩阵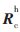 。同理控制机械手沿机械臂末端坐标系的Zh-、Yh+、Zh+、Yh-、Zh-、Yh-方向移动10 mm,每两次移动就可确定一个
。同理控制机械手沿机械臂末端坐标系的Zh-、Yh+、Zh+、Yh-、Zh-、Yh-方向移动10 mm,每两次移动就可确定一个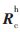 。旋转矩阵的多次实验结果数据如表1所示,其中最大偏差为旋转矩阵的计算值与平均值之间的偏差矩阵中的最大值。从表1可看出旋转矩阵的偏差是稳定的,取平均值作为
。旋转矩阵的多次实验结果数据如表1所示,其中最大偏差为旋转矩阵的计算值与平均值之间的偏差矩阵中的最大值。从表1可看出旋转矩阵的偏差是稳定的,取平均值作为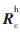 的标定结果。即:
的标定结果。即:
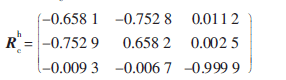
3.2 手眼关系平移向量的标定实验
在求平移向量之前,需通过激光笔来获取工件平台上特征点的基坐标,因此先对激光笔在机械臂末端坐标系x、y轴的坐标位置hxp、hyp进行标定。通过多次标定得到的数据结果如表2所示,其中偏差为(hxp,hyp)T的实验计算值与平均值之间的差值。
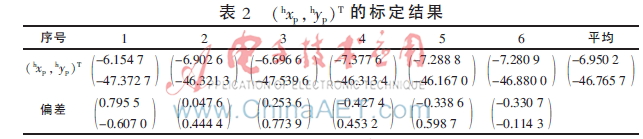
由表2可以看出,实验得出的hxp、hyp比较稳定,取平均值作为hxp、hyp的标定结果。即:
hxphyp=-6.950 2-46.765 7
在求得hxp、hyp后,控制机器人使激光射线打在工件平台上基坐标待求的特征点P上,从控制器中获取当前机器人的关节变量求得机械臂末端的位姿参数,由式(12)即可求得P点的基坐标。
接着对手眼关系平移向量进行标定:控制机械手使工件平台上基坐标已知的4个特征点置于场景中,从控制器中获取当前机器人的关节变量求得![9`NN$K1]EL{]O0IGN{JS)~9.jpg 9`NN$K1]EL{]O0IGN{JS)~9.jpg](http://files.chinaaet.com/images/2016/02/17/6359133538348992578108643.jpg) ,从图像上获取这些特征点的图像像素坐标,这些特征点的zc值按参考文献[2]的方法另外求取,
,从图像上获取这些特征点的图像像素坐标,这些特征点的zc值按参考文献[2]的方法另外求取,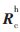 、M均已知,由式(19)即可求得手眼关系的平移向量
、M均已知,由式(19)即可求得手眼关系的平移向量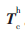 。平移向量的标定结果数据如表3所示,其中最大偏差为平移向量的计算值与平均值之间的偏差向量中的最大值。
。平移向量的标定结果数据如表3所示,其中最大偏差为平移向量的计算值与平均值之间的偏差向量中的最大值。
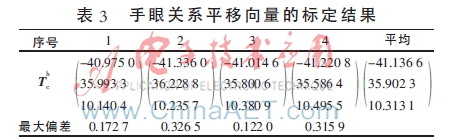
由表3可看出,平移向量的最大偏差小于0.5 mm,取平均值为其标定结果。即:
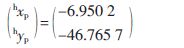
3.3 标定结果测试

选取工件平台上的4个点作为测试点,且将特征点置于不同的场景中,如图4所示,通过求取特征点的基坐标以求得这4个特征点两两之间的距离,实验结果数据如表4所示,其中实际值为由游标卡尺直接测量所得特征点之间的间距。
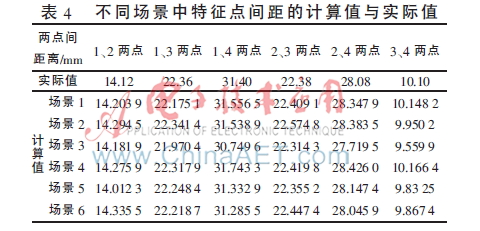

由表4可得不同场景中特征点间距计算值与实际值的误差曲线,如图5所示。从图5可以看出,特征点间距计算值与实际值的误差在±0.8 mm之间,说明所标定的手眼关系的旋转矩阵 和平移向量
和平移向量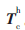 精度较高,可满足机器人的工件定位与自动抓取的要求。
精度较高,可满足机器人的工件定位与自动抓取的要求。
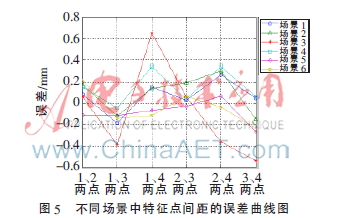
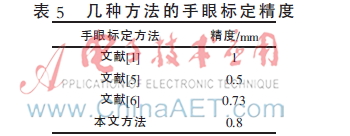
表5列出了本文方法和其他文献方法的手眼标定精度。从表5可以看出,参考文献[5]的标定精度最高,达到了0.5 mm,但其标定过程要求机器人的外臂坐标系到机器人基坐标系的旋转矩阵以及末端执行器的高度保持不变,具有一定的局限性。而参考文献[1]和参考文献[6]的手眼标定方法在求解平移向量时均需要机器人做旋转运动,并且不能仅仅只绕某一轴旋转,若仅绕某一轴旋转将无法求出平移向量。在标定精度方面,参考文献[6]的标定精度与本文方法相当,而参考文献[1]和参考文献[5]的标定精度均低于本文方法。
4 结论
本文提出了通过固定在机械臂末端的激光笔来获取工件平台上特征点的基坐标,以此来标定手眼关系的平移向量;通过场景中的两个特征点,通过精确控制机械臂做2次特定的平移运动即可标定出手眼关系的旋转矩阵。实验结果表明,本文方法的标定精度较高(±0.8 mm),可满足一般机器人工件自动抓取、跟踪控制等作业的使用要求。此外,本文提出的方法对于平移向量的标定,只需要求机器人末端手臂垂直于工件平台,并使固定在该臂上的激光笔的射线平行于该臂坐标系的z轴,这对于大多数的机器人都是易于实现的,因此本文的方法精度高,适用范围广。
参考文献
[1] MA S D. A self-calibration technique for active vision systems [J]. IEEE Transactionsons on Robotics and Automation,1996,12(1):114-120.
[2] 杨广林,孔令富,王洁.一种新的机器人手眼关系标定方法[J].机器人,2006,28(4):400-405.
[3] SHIU Y C, AHMAD S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB[J]. IEEEE Transactions on Robotics & Automation, 1989,5(1):16-29.
[4] TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEEE Transactions on Robotics & Automation, 1989,5(3):345-358.
[5] 戚芳,席锋.简便高精度的机器人手眼视觉标定方法[J].传感器与微系统,2006,25(1):27-29.
[6] 张黎烁,赵志梅.基于主动视觉的结构光手眼系统自标定方法[J].科学技术与工程,2014,14(9):202-206.

