摘 要： 对于边界显著的图像，用二值图像代替灰度图像进行SIFT特征匹配，节约了运行时间。同时在SIFT算法中用128维的特征描述子进行特征描述影响了算法的实时性，用欧氏距离进行匹配对算法的准确性有一定的影响。提出了一种改进SIFT算法，用64维的特征描述子以及加权的欧式距离进行匹配。实验结果表明，所提出的改进方法在提高准确率的同时还减少了运行时间。
关键词： SIFT算法；二值图像；特征描述子；加权欧式距离
0 引言
图像匹配是将两幅或多幅在不同条件下拍摄的图像进行相互匹配。目前它在模板匹配定位[1]、导航、医学影像分析和计算机视觉[2]等多个领域有广泛的应用。
目前图像匹配的方法主要分为基于灰度的匹配方法[3]和基于特征的匹配方法[4]。前者直接利用图像灰度进行匹配，算法比较简单，但对噪声等干扰比较敏感，匹配效率普遍较低。后者对形变、旋转及平移的适应性较好。SIFT（Scale Invariant Feature Transform）算法是一种相对稳定的局部特征匹配算法[5]。
SIFT算法虽然可以对旋转和平移在图像匹配过程中的干扰进行处理，但它也存在算法效率低、匹配精度差等问题。本文提出了一种对于边界显著图像的改进的新方法，利用二值图像代替灰度图像，简化了图像信息，利用64维特征描述子并且用加权的欧式距离进行匹配。试验证明该方法不仅提高了算法的精度和准确率，而且在边界显著的图像的匹配中也有较好的适用性。
1 SIFT算法
SIFT算法主要包括尺度不变空间的特征点检测、特征点信息描述、特征向量的匹配。
1.1 尺度不变空间的特征点检测
在对尺度不变空间进行特征点检测时，首先要提取出尺度不变空间的极值点，然后精确定位特征点，最后为每个特征点分配方向。
尺度不变空间的极值点检测。通过高斯核产生多尺度空间的核[6]。一幅二维图像I（x，y）与尺度可变高斯函数G（x，y，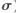
）做卷积，可得到该图像的尺度不变空间L（x，y，
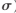）如式（1）所示。
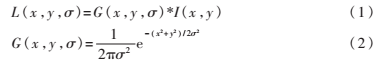
其中，（x，y）表示图像中像素点的坐标，*是卷积，σ是尺度空间因子。通过对高斯尺度空间进行采样来建立高斯金字塔；再对相邻两层的高斯金字塔相减，生成高斯差分尺度空间（DOG scale-space）金字塔，即：
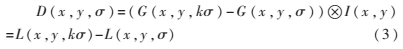
如果某点比DOG尺度空间中本层的8个点以及上下两层的18个点都大或者都小，则把该点作为图像在该尺度下的一个候选特征点，如图1所示。
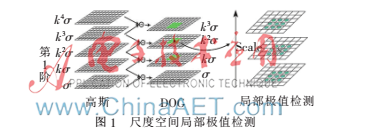
在得到候选特征点之后，要检测每个候选特征点的稳定性，把检测通过的特征点作为SIFT特征点。首先要对特征点中的边缘响应点和对比度较低的点进行去除，然后构造一个三元二次函数，利用此函数来更加精确特征点的位置和尺度。
为了使SIFT算法具备旋转不变性，需要为每个特征点分配方向。像素点（x，y）处的梯度值与方向分别为：
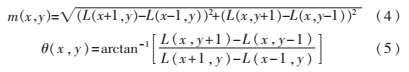
其中，L中的尺度是该特征点所在的尺度。
在实际计算中，利用取值在0~360°范围内的梯度直方图来对特征点的邻域像素的梯度方向进行统计，其中每10°代表着一个方向，共分为36个方向，并把直方图中的峰值作为该特征点的方向。至此，完成尺度不变空间的特征点检测，每一个特征点都包含了方向、尺度和位置信息。
1.2 特征点信息描述
为了确保算法具有旋转不变性，要将坐标轴旋转到特征点的方向。然后在特征点的周围取16×16的像素窗口，在4×4的小块图像上计算8个方向的梯度方向直方图，对每个梯度方向的累加值进行描绘，构成一个种子点。用16个种子点来描述每个特征点，就此形成了128维的SIFT特征描述子。
1.3 特征向量的匹配
SIFT特征向量生成之后，利用欧氏距离，即d（u，v）=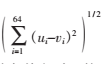
进行匹配。按一定顺序选取主图像中的所有特征点，然后利用欧式距离计算该特征点与待匹配图像中所有特征点的距离，提取出最近距离和次近距离，如果最近的距离比次近的距离小于某个设定的阈值，则认为这两个特征点是匹配点对。
2 本文提出的改进算法
2.1 图像二值化
在原始SIFT算法中，利用原图像的灰度图像来构造DOG尺度空间。而对于边界显著的图像，它的边界和轮廓信息比较重要，背景信息相对可以忽略，如果使用灰度图像来进行SIFT特征匹配，会使算法在背景信息上浪费时间。
本文利用二值图像代替灰度图像，由于二值图像的灰度值均为1或0，这对于极值点的选取和特征向量的描述与匹配都有所简化。
2.2 改进后算法的特征描述子
由于SIFT特征向量高达128维，这为后来的匹配工作带来了很大的计算量[7]，但是多数降维方法由于没有考虑到SIFT的特点进行降维，从而导致它的匹配效率下降。本文利用的降维方法从SIFT的自身特点出发进行降维，在匹配效率不变的情况下成功地节约了匹配时间。
如图2所示，对于一个种子的8个方向的梯度方向直方图的累加值a0，a1，…，a7，用4个方向b0，b1，b2，b3来表示，如图3所示。其中
b0=|a0-a4|（6）
b1=|a1-a5|（7）
b2=|a2-a6|（8）
b3=|a3-a7|（9）
这样描述每个种子的累加值的数量由8个降到了4个，但是这4个累加值仍然包含了8个累加值中所有的信息，所以即使特征描述子由128维降到64维，也不影响对特征点信息的描述，对匹配效率也不产生影响。在特征匹配时，由于特征向量的维数减少了一半，因此此方法为计算距离节约了时间，提高了算法的实时性。
2.3 用加权的欧式距离进行匹配
利用欧氏距离进行相似性度量的方法能够解决匹配的问题，但是不难发现生成的64维的描述子之间是不等价的，离特征点越近的种子所生成的描述子起的作用越大。因此本文的改进方法为用加权的欧式距离代替欧式距离进行图像匹配，从而提高匹配效率。
加权的欧式距离，即d（u，v）=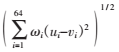
，它考虑了不同维之间不同的重要性，本文选择离特征点较近的4个种子生成的16维的描述子，使它们在匹配时的权重
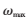取较大值，其余的12个种子生成的48维的描述子权重
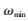取较小值。经过大量的实验发现，随着
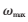的逐渐增大，相匹配的特征点的数量会逐渐减少，同时考虑到匹配的特征点数量和算法精度的因素，本文认为当阈值
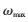∈[1.01，1.50]时匹配效果较好。
3 实验与分析
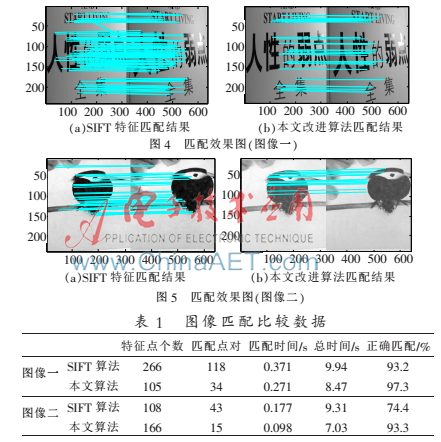
本文设计了一系列的实验来检测本文改进算法的性能。为了更好地对实验结果进行比较，所有实验都是利用MATLAB7.10编程，运行在配置为Intel（R）core（TM）2 Duo CPU P7350@2.00 GHz、操作系统为Microsoft Windows 7的微机平台上。选择边界显著的图像作为匹配对象。为了使本文改进算法的性能得到更加全面的体现，实验结果从特征点个数、匹配点对、特征点匹配时间、算法运行总时间以及正确匹配率5个方面对改进算法与原算法进行比较，如图4、图5和表1所示，其中改进的SIFT算法取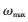
=1.15。
通过分析实验数据和匹配结果可以发现：改进的算法由于用二值图像进行匹配，简化了图像信息；同时用64维的特征描述子，大大节约了匹配的时间；用加权的欧式距离提高了算法的匹配率。由此可见本文的改进算法运算速度更快、准确率更高。
4 结论
通过对SIFT算法的深入研究，本文就SIFT算法自身的不足进行了改进，利用二值图像进行特征匹配，同时在不影响匹配效率的前提下对SIFT算法成功地进行了降维，最后用加权的欧式距离作为相似性度量进行匹配。经过大量的实验不难发现，对于边界显著的图像，本文改进的算法在匹配时间和匹配效率上都要优于原始的SIFT算法。但本文改进算法也有不足之处，匹配的特征点对相对较少，因此对该算法处理的图像类型有一定的限制，所以如何改进此问题是下一步工作的重点。
参考文献
[1] 吴立德.计算机视觉[M].上海：复旦大学出版社，1993.
[2] 吴毅良.一种基于SIFT和SUSAN特征的图像匹配方法[J].微型机与应用，2011，30（12）：33-35.
[3] MORTANI M，SATIONH F. Image template matching based on ratio of mean and central pixel in local area[J].Proceedings of the SPIE The International Society for Optical Engineering， 2007，67（94）：1-6.
[4] ZITOVA B， FLUSSER J. Image registration methods： a survey[J]. Image and Vision Computing， 2003，21（11）：977-100.
[5] DAVID G L. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision（S0920-5691），2004，60（2）：20.
[6] LINDEBERG T. Scale-space theory： a basic tool for analyzing structures at different scales[J]. Journal of Applied Statistics， 1994，21（2）：225-270.
[7] Zhu Hongbo， Xu Xuejun， Wang Jing， et al. A rapid automatic image registration method based on improved SIFT[J]. Procedia Environmental Sciences， 2011，11（A）：85-91.