摘 要: 在对目标进行分类识别过程中,对其特征的有效提取直接影响最后分类的精度。针对此类问题,提出了基于Tri-training算法对图像进行多特征融合分类,通过利用Principal Component Analysis(PCA)主成分分析法,并结合目前比较实用的半监督学习Tri-training算法对图像显著目标进行分类,其中Tri-training算法是以Support Vector Machine(SVM)、Na?觙ve Bayes(NB)、Back Propagation(BP)为基分类器,将图像的多特征数据值作为图像在Tri-training分类器的输入对分类器进行训练和测试。实验表明,在进行了有效的预处理之后,再对样本进行多特征融合在一定程度上明显提高了分类精度。
关键词: 分类器;多特征融合;半监督;显著目标
0 引言
半监督学习是近年来提出的一种新的学习策略,它不仅有效结合了监督学习和非监督学习的优点,而且完善了它们的不足。它通过同时使用标记样本和未标记样本的数据,然后利用未标记样本的信息数据来帮助其建立学习模型,使其可以获得很好的学习泛化性能和学习效果。所以在近年来该理论及其算法得到快速的发展和应用,Blum和Mitchell提出的Co-training算法[1],通过使用两个不同的分类器来实行协同训练,然后再将单个分类器所产生的新标记数据加入到另一个分类器中,通过迭代的方法,不停地扩充有标记样本集并反复训练。但是该算法不仅要求其数据属性可以分为两个不同的子集,而且要求其中每个子集能独立训练产生出分类器,所以在实际应用中很难得到满足。Zhou等人提出的Tri-training算法[1],它没有充分冗余视图的局限,同时也不需要采用不同的分类方法,其实用性更广。将Co-training算法和Tri-Training算法结合的SVM分类方法,也可以获得很好的分类精度。
为了提高对图像中显著目标的分类精度,本文提出了基于Tri-training算法对目标进行多特征融合分类的方法,首先对图像中的目标进行预处理,消除图像中的噪声干扰,同时有效克服其强度敏感性。然后在此基础上分别提取中心矩特征,仿射不变矩特征以及其灰度共生矩特征,然后再利用PCA方法将以上特征融合,最后基于Tri-training算法进行分类。
1 特征提取
1.1 数据预处理
在对图像数据实行有效的预处理过程中,一般主要对其实行去噪处理。本文主要利用小波方法对图像实行有效的降噪处理。小波变换降噪方法通过将数据变换到其小波域中,然后再利用小波分解获得的高频系数将其去除,最后再对图像信号进行小波反变换来达到降噪目的。其公式如下:
g(x,y)=f(x,y)+n(x,y)(1)
其中g(x,y)为要得到的理想图像,f(x,y)为输入图像,n(x,y)为噪声,通过频域变化将噪声去除就得到了想要的理想图像。
1.2 图像中心矩特征提取
假设x={x(i),i=0,1,2,…,I-1}表示距离像幅度,其中x(i)为第i+1个距离单元的回波幅度,I为距离单元的个数,然后对其归一化处理可得:

f=[f(1),f(2),…,f(J-1)]T=[W2,W3,…,WJ]T(4)
其中中心矩WJ的幅度与阶数关系为递增关系,为了能够有效地抑制指数增长造成的影响,一般通过对中心矩作极差变换来达到消除数量级造成干扰的目的。在对中心矩特征作向量极差变换时,实质上是做了归一化处理,从而有效地解决了特征不在同一个数量级的问题。所以可得其中心矩特征为f=[f(1),f(2),…,f(J-1)],其中J表示中心矩的最高阶数。
1.3 图像灰度共生矩阵特征提取
灰度共生矩阵一般定义为从灰度级为i的点离开某个固定位置关系d=(Dx,Dy)达到灰度为j的概率。这里用Pd=(i,j)(i,j=0,1,2,…,L-1)来表示灰度共生矩阵。其中L指图像的灰度级,i,j分别表示像素的灰度。图像中像素间的距离和方向由d的值决定。?兹为灰度共生矩阵的生成方向,通常取0°,45°,90°和135°四个方向。灰度共生矩阵的像素对如图1所示。

当选定像素间位置关系d后,就能基于关系d生成灰度共生矩阵[2]。
Pd= Pd(0,0) Pd(0,1) … Pd(0,j) … Pd(0,L-1) Pd(1,0) Pd(1,1) … Pd(1,j) … Pd(1,L-1) … … … … … … Pd(i,0) Pd(i,1) … Pd(i,j) … Pd(i,L-1) … … … … … …Pd(L-1,0) Pd(L-1,1) … Pd(L-1,j)… Pd(L-1,L-1)(5)
1.4 图像仿射不变特矩特征提取
一般二维仿射线性变换的数学变换模型可表示为:
x′y′=Axy+b(6)
假设p是坐标平面上任一点,p′点是其仿射线性变换对应点,变换后坐标系下的两点坐标可表示

如果通过归一化中心矩来获得仿射不变矩,只需要合适的扭曲不变性和拉伸不变性就可以实现仿射变换的不变性。通过利用构造的中心矩多项式方法,可达到消除仿射变换矩A的目的,这样就能实现一般情况下的仿射不变性。这里是利用Jan Flusser等人构造的六个仿射不变矩变量来作为目标图像的特征不变量[3]。

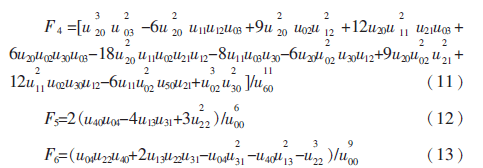
2 特征融合
PCA的基本思想是用一组维数最少的特征以最精确的方式描述原始样本特征[4-5]。仿真实验中从图像中提取三种有效特征,然后使用主成分分析法再将三种特征融合成一种综合特征对目标进行分类。实验取每类样本100张图片,一共两类样本数据,其中每一组样本数据中包含7维中心矩特征、6维仿射不变矩特征以及3维灰度共生矩特征。将上述三种特征生成一个16维的特征向量为x=(?准1,?准2,…,?准16)T,那么由200个特征向量构成的特征矩阵为X=(x1,x2,…,x200),其中向量xk表示第k张样本图像的中心矩特征,仿射不变矩特征及灰度共生矩特征组成列向量。实验仿真中先将三种特征数据进行串联,然后通过PCA来将串联后的数据进行有效的融合。目的有两方面:一是将三种特征数据中的相关性消除;二是将三种特征数据从高维矢量降为低维矢量。
3 基于Tri-training的图像目标分类

基于Tri-training算法的多特征融合图像分类流程图如图2所示。将图像数据转换成算法程序能够处理的数据格式(xls文件)并输入到Tri-training算法的MATLAB程序中,由算法进行样本集的划分。当完成初始的三种基分类器之后,按百分比输入已标记样本,然后通过三个基分类器对未标记样本进行相互标记以获得置信度高的样本,再加入到已标记样本中进行模型的训练。以此迭代直至结束,最后获得由三个基分类器组成的集成分类器。在测试阶段,通过三个分类器分别对测试样本集进行有效的分类,使用多数投票法来获得最后的分类结果。
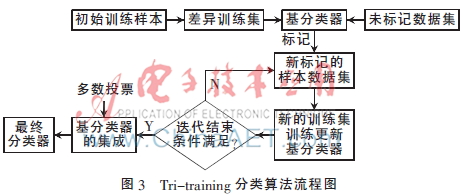
Tri-training分类算法流程图如图3所示。Tri-training[4]算法采用三个基分类器,再通过随机采样算法bootstrap来获得存在差异的训练数据子集,从而能够有效地保证基分类器之间的差异性。在Tri-training训练结束后,采用多数投票法对三个分类器进行集成,得到最终的分类器进行分类。
4 实验结果与分析
本文中选取飞机和越野车各100张照片作为实验数据,首先提取图像的中心矩特征、放射不变矩特征和灰度共生矩特征,再将这些数据融合得到一个多特征数据来作为Tri-training分类器的输入数据,实验中基于MATLAB 7.0平台进行仿真。部分样本如图4所示。

4.1 样本分配
选用25%的特征数据作为测试样本集,剩余的75%作为训练样本集。在训练样本集中,未标记样本的比例依次选用80%,60%,40%和20%进行测试和比较。Tri-training算法中采用了SVM,NB,BP作为分类器。
4.2 算法的性能评价标准
采用算法对于测试集的分类错误率作为分类器的评价指标。

其中,E是算法分类错误率,Ncorrect是分类正确的样本数目,N是总样本数。
4.3 实验结果
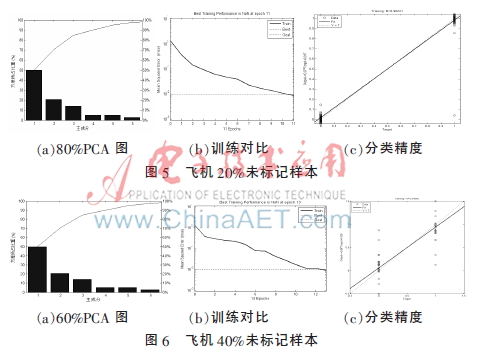
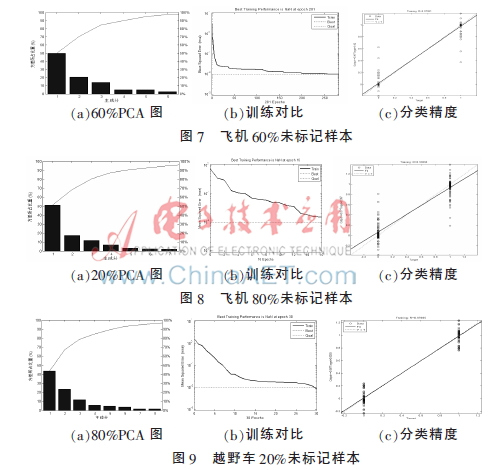

实验中对未标记样本的比例依次选用80%,60%,40%和20%进行测试和比较,结果如图5~图12所示。以下各图中,(a)为PCA融合得到的方差图,(b)为训练之后与最优线的比较,(c)是最后分类的精度。
表1是在4种不同百分比下未标记样本的半监督学习(PCA+Tri-training)与对应的PCA特征融合分类错误率的比较。
从表1中可以看出,当标记的样本比较多时,PCA多特征融合法与基于Tri-training算法的PCA多特征融合法的分类精度差不多,但是当样本开始减少时,就能看出两种方法的差异性,所以在少数样本情况下第二种方法更实用,分类精度更高,操作性很强。
5 结束语
本文主要是将机器学习领域的Tri-training半监督学习方法应用在图像的显著目标分类,并基于Tri-training算法提出了与多特征融合相结合的图像分类方法,通过有效地将图像的中心矩特征、仿射不变矩特征和灰度共生矩特征进行融合,利用SVM,NB,BP三个基分类器进行协同训练,达到了很好的分类效果。仿真结果表明其在小样本分类中具有很好的分类效果。
参考文献
[1] 周志华.机器学习及其应用2007[M].北京:清华大学出版社,2007.
[2] 陆丽珍,刘仁义,刘南.一种融合颜色和纹理特征的遥感图像检索方法[J].中国图象图形学报,2004,9(3):328-332.
[3] 楚稼,张桂林.基于颜色和边缘信息融合的背景建模方法[J].计算机工程,2008,34(4):42-45.
[4] LOWE D G. Distinctive image features from scale invariant key points[J]. In Journal of Computer Vision, 2004,60(2): 91-110.
[5] 谢辉,陆月明,孙松林.基于半监督学习的一种图像检索方法[J].计算机应用研究,2013,30(7):2210-2212.

