摘 要: 提出一种分割灰度不均匀单目标相似图像组的新模型。该模型结合组相似活动轮廓模型(ACGS)和不均匀性嵌入式活动轮廓模型(InH_ACM),同时考虑了图像的灰度、纹理和形状的特征,能有效分割灰度不均匀的图像组,处理图像中的误导信息。另外,采用在GB显著图上自动定位初始轮廓的方法,重新定义了平衡灰度一致性能量和纹理一致性能量的权重。实验结果表明,该方法在分割精度和收敛速度上都有优势。
关键词: 图像分割;相似图像组;ACGS模型;InH_ACM模型;GB显著图
0 引言
研究发现对于存在误导信息(如背景中有树枝、花丛等)的单张图像,很难得到理想的分割结果。因此,研究者们开始尝试利用多张图像间的相似性,排除干扰。2013年,Zhou Xiaowei等人提出组相似活动轮廓模型[1](Active Contours with Group Similarity,ACGS),专门针对目标形状相似的单目标图像组进行分割,可以有效地修正由于图像中干扰信息导致的分割错误,其避免了人工标记大量带注释数据,可视为一种无监督的先验形状模型,但该模型一般只对灰度均匀的图像组有效。为了分割灰度不均匀图像,近年来学者们也提出了各种改进模型[2],这些模型主要利用局部卷积消除局部不均匀性,一般只对灰度变化缓慢的图像有效,对于灰度变化剧烈的图像是无效的。本文采用不均匀性嵌入式活动轮廓模型[3](Inhomogeneity-embedded Active Contour,InH_ACM)来处理灰度不均匀图像问题。
本文结合ACGS模型和InH_ACM模型,提出一种分割灰度不均匀单目标相似图像组的新模型,称为不均匀性嵌入式组相似活动轮廓模型(Inhomogeneity-embedded Active Contours with Group Similarity,InH_ACGS)。该模型同时利用图像的灰度和纹理特征,并在形状相似约束下快速收敛,同时对图像中干扰信息导致的分割错误有一定的修正作用。另外,采用在GB显著图[4]上自适应获取初始轮廓的方法,并重新定义了灰度一致性和纹理一致性权重的计算方式。在实验部分,通过两组真实相似图像组的分割结果证明了本文模型分割不均匀图像组的效果优于另外两种模型,收敛速度也更快。
1 相关背景
1.1 ACGS模型
给定一组相似图像I1,…,In,要获取图像的目标轮廓C1,…,Cn。为了保证轮廓间的相似性,Zhou Xiaowei等人提出以下模型:
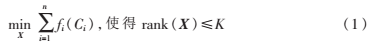
其中,X=[C1,…,Cn];K是一个预设常数,K越小目标形状越相似;fi(Ci)是CV模型[5]的能量泛函,表达式如下:
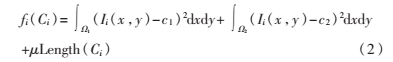
其中,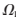 和
和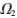 表示曲线Ci的内部和外部区域;c1、c2分别表示曲线Ci内部和外部的灰度均值;Length(Ci)为曲线Ci的长度;
表示曲线Ci的内部和外部区域;c1、c2分别表示曲线Ci内部和外部的灰度均值;Length(Ci)为曲线Ci的长度;![_(L2{P7VNA(87]TGI6$4EZ6.png _(L2{P7VNA(87]TGI6$4EZ6.png](http://files.chinaaet.com/images/2016/02/20/6359160127415900003439703.png) ≥0为常数,是长度项的权重。
≥0为常数,是长度项的权重。
式(1)中用核范数代替秩算子,得到以下目标函数:

其中,‖X‖*表示X的核范数,也就是X奇异值的和;λ是形状相似性权重,λ越大轮廓间的相似性越强。
1.2 InH_ACM模型
图像I中的任意像素点p=(px,py),I(p)为该像素点的灰度值,窗口大小k∈Z,k≥1,其中Z为整数,此处固定k,定义像素p的空间邻近方形邻域为:
N(p)={q∈I:|px-px|≤k,|py-qy|≤k}(4)
在形式上,该领域内的像素点可以分为以下两类:
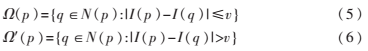
其中,![Z~8@BRPDMC]NKMV24T9WT]F.png Z~8@BRPDMC]NKMV24T9WT]F.png](http://files.chinaaet.com/images/2016/02/20/6359160146048600006142601.png) =N(p),v>0是给定的阈值。
=N(p),v>0是给定的阈值。
像素不一致因子PIF(Pixel Inhomogeneity Factor)定义如下:

其中,|·|表示集合中包含的元素个数。所有像素点PIF值组成的矩阵对应一张反映图像纹理信息的InH(Inhomogeneity)图(如图1(b)所示)。
在CV模型框架下,嵌入InH得到以下纹理一致性能量泛函:
![]]FFW{`MTJ$S]R_ZW_[D_39.png ]]FFW{`MTJ$S]R_ZW_[D_39.png](http://files.chinaaet.com/images/2016/02/20/6359160154254500001556076.png)
其中,PIF(x,y)表示坐标为(x,y)像素点的PIF值。i1和i2分别表示曲线C内部和外部的PIF均值。
再联合传统CV模型的全局灰度一致性能量函数:
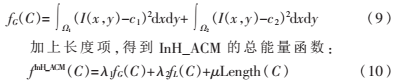
其中,λ1≥0、λ2≤1是平衡灰度一致性和纹理一致性能量项的权重。
InH_ACM模型能有效分割灰度不均匀图像,但对于图像中目标和背景的灰度和纹理同时有相似部分的情况,往往会造成错误分割。如图1中小鸟和木桩的灰度和纹理都很相似,会被误认为是同一分割目标。

2 本文模型
2.1 InH_ACGS模型
本文结合以上两种模型,建立以下能量泛函:
![8VFCA_80MW8X]NYXRH9]6T0.png 8VFCA_80MW8X]NYXRH9]6T0.png](http://files.chinaaet.com/images/2016/02/20/6359160164251800008476700.png)
其中,fiInH_ACM(Ci)是InH_ACM模型的能量泛函。
将式(11)简写为以下形式:
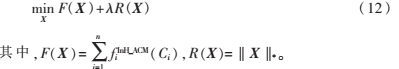
参考文献[1]中已经给出了式(12)的具体算法步骤,根据该算法可以直接求解。唯一不同的是,在计算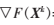 时,
时,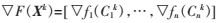 ,计算如下:
,计算如下:
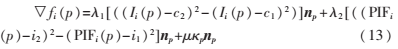
其中,p是曲线Ci的坐标,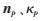 分别是在p点的法向量和曲率。
分别是在p点的法向量和曲率。
2.2 GB显著图获取初始轮廓曲线
本文首先采用GB方法[4]输出显著图,再在显著图上使用CV模型获取初始轮廓曲线。通过GB方法获得的显著图,其显著性区域(即高亮区域)大致就是所要分割的目标区域,所以通过该方法获取的初始轮廓曲线基本在分割目标附近(如图1(c)、(d)、(e)所示)。GB方法输出显著图的具体步骤参见参考文献[4],在作者的网页上有可直接运行MATLAB代码。
3 实验
3.1 实验结果
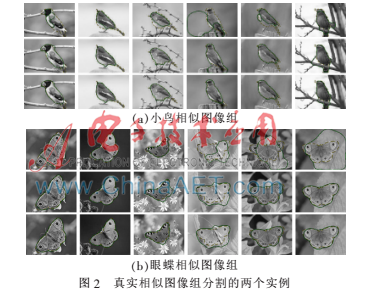
本节通过两组真实相似图像组的实验比较ACGS模型、InH_ACM模型和本文InH_ACGS模型的分割结果。对于两组实验,选取相同的长度项权重![)T[PS4$YWF8_6$G6%]4QKKK.png )T[PS4$YWF8_6$G6%]4QKKK.png](http://files.chinaaet.com/images/2016/02/20/6359160191665100008786631.png) 为2,计算PIF值的窗口k大小为5,阈值v采用参考文献[3]的方法自适应计算得到。另外,图2中图像组(a)、(b)使用的形状相似性权重λ分别为10、15。图中,分别由6张灰度不均形状相似的小鸟或眼蝶图像组成,每个实例的第一至第三行分别表示ACGS模型、InH_ACM模型和本文InH_ACGS模型的结果,黑色实线为模型输出曲线。
为2,计算PIF值的窗口k大小为5,阈值v采用参考文献[3]的方法自适应计算得到。另外,图2中图像组(a)、(b)使用的形状相似性权重λ分别为10、15。图中,分别由6张灰度不均形状相似的小鸟或眼蝶图像组成,每个实例的第一至第三行分别表示ACGS模型、InH_ACM模型和本文InH_ACGS模型的结果,黑色实线为模型输出曲线。
需要特别说明的是,本文重新定义了灰度一致性权重λ1和纹理一致性权重λ2的计算公式,参见3.2节。
图2(a)、(b)的第一行结果显示,ACGS模型对于灰度不均匀的图像组几乎无法正确分割,只考虑灰度特征是远远不够的;而第二行中,InH_ACM模型能够大致找到分割目标的边界,但是当图像目标和背景的灰度和纹理都有一定相似性时容易造成错误分割,例如图2(a)中第二行的第1、4、6列和图2(b)中第二行的第3、4列,分割结果会受到背景枝干、木桩、花丛等的影响;第三行为本文InH_ACGS模型的分割结果,同时考虑灰度、纹理和形状特征,能够在一定程度上排除背景环境因素的干扰,得到比较准确的分割结果。虽然本文模型对目标轮廓有一定的修正作用,但对于像图2(b)中第4张这样目标和背景的灰度和纹理的对比度都非常低的弱边界图像效果并不十分明显。另外,在收敛速度上,由于该模型的形状约束影响,避免轮廓曲线重新初始化,保持轮廓曲线间的相似性以至于不会偏离太远,因此能够快速地演化到目标边界上。两组图像在InH_ACM模型和本文模型下的收敛时间分别为:66.06 s、49.60 s和65.96 s、60.46 s。
为了评估模型分割结果的好坏,本文采用F测度来对其评估,其定义为:
![M5%9@0ML]RJ{P$FW~`K3J6S.png M5%9@0ML]RJ{P$FW~`K3J6S.png](http://files.chinaaet.com/images/2016/02/20/6359160197256200002682306.png)
其中,A是模型分割目标,B是基准目标。F测度越大说明模型的分割结果越好。表1中显示本文模型的分割效果比另外两种模型都好,这也证明了将ACGS模型与InH_ACM模型相结合能发挥两者的优势,得到更好的结果。

3.2 参数设置
本节给出一个设置灰度一致性权重和纹理一致性权重λ2的方法。在原始图像和InH图中,首先分别定义初始轮廓内外的灰度均值对比度和PIF均值对比度为:
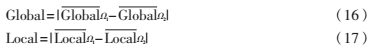
其中, 分别表示轮廓内外灰度均值,
分别表示轮廓内外灰度均值, 分别表示轮廓内外PIF均值。然后,定义λ1、λ2,如下:
分别表示轮廓内外PIF均值。然后,定义λ1、λ2,如下:
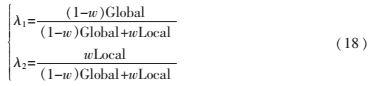
其中,w表示平衡原始图像和InH图的权重,w∈[0,1],本文实验中w取值为0.5。
4 结论
本文模型同时考虑图像组的灰度、纹理和形状信息,能够比较准确地分割出不均匀图像组中相似目标的边界,对于背景干扰信息也有一定的修正作用,并且在形状约束下快速收敛。但该模型也存在一些不足,如果使用GB显著图获取的初始轮廓曲线位置不适合,可能会影响分割的结果。另外,本文模型在处理弱边界图像时还有待改进之处。
参考文献
[1] Zhou Xiaowei, Huang Xiaojie, DUNCAN J S, et al. Active contours with group similarity[C]. 2013 IEEE Computer Vision and Pattern Recognition(CVPR), 2013:2969-2976.
[2] 汪方正,向德辉.基于演化曲线自适应的图像分割模型的研究[J].计算机技术与应用,2014,40(11):132-135.
[3] Dai Lingzheng, Ding Jundi, Yang Jian. Inhomogeneity-embedded active contour for natural image segmentation[J]. Pattern Recognition, 2015,48(8):2513-2529.
[4] HAREL J, KOCH C, PERONA P. Graph-based visual saliency[J]. Advances in Neural Information Processing Systems, 2007,19(1):545-552.
[5] CHAN T, VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing,2001,10(2): 266-277.

