摘 要: 时间序列的维数比较大,直接对时间序列进行聚类性能不理想。如何提高时间序列的聚类性能,是主要研究点。首先使用邻域保持嵌入对时间序列样本维数约简,然后对维数约简后的数据进行聚类融合,最后将它的聚类性能与已有方法如主成分分析、分段聚合近似进行比较。实验表明,所提出的算法更能提高聚类性能。
关键词: 时间序列;聚类融合;维数约简;邻域保持嵌入
0 引言
时间序列是一种高维且随着时间变化而变化的数据。时间序列聚类在风险管理、车辆检测[1]、隧道通风控制、交通流等领域广泛应用。
苏木亚等人[2]提出了基于主成分分析(Principal Component Analysis,PCA)的时间序列聚类方法,但是PCA是线性方法,现实数据集往往具有非线性特征;李海林等人[3]先用分段聚合近似(Piecewise Aggregate Approximation,PAA)对时间序列降维,然后进行聚类,但是PAA没有考虑样本之间的内在关系。邻域保持嵌入(Neighborhood Preserving Embedding,NPE)[4]是局部线性嵌入(Locally Linear Embedding,LLE)[5]的线性近似,它清晰地考虑了数据的流形结构,约简后的数据可以最优地保持原数据集的局部邻域信息,并考虑了样本之间的内在关系。
针对单一聚类算法存在结果不稳定的问题,现在趋向于融合多个聚类的结果,即聚类融合。本文提出了一种基于NPE的时间序列聚类融合算法,实验结果表明,本文提出的算法与已有方法相比,更能提高聚类性能。
1 背景
1.1 邻域保持嵌入
设原始数据集X={x1,x2,…,xn}?奂Rl,NPE[4]找到变换矩阵A。使用A将X映射到Y={y1,y2,…,yn}Rd,(d<<l),能够保持X的局部结构。
(1)构造邻域图G。如果xj在xi的k近邻中,就在两个点之间放一条有向边。
(2)计算加权矩阵W。通过解决最小化问题得到点xi到xj之间边的权重Wij;如果xi与xj之间没边,则Wij=0。

其中,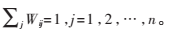
(3)计算映射。通过解决一般特征值问题来获得转换向量a:
XMXTa=λXXTa(2)
其中,X=(x1,…,xn),M=(I-W)T(I-W),I=diag(1,…,1)。假设A=[a0,a1,…,ad-1],特征值排序后为0≤λ0≤…≤λd-1。得到y:yi=ATxi,其中yi是d维向量,A是l×d矩阵。
1.2 基于互信息的聚类成员的权值
聚类成员Pa、Pb类标记用{P1a,P2a,…,Pka}和{P1b,P2b,…,Pkb}表示。设Pia中有ni个元素,Pjb中有nj个元素,Pia和Pjb中相同元素有nij个。互信息ФMI为[6]:
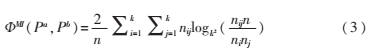
每个聚类成员的平均互信息为:
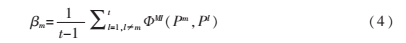
βm越大,聚类成员Pm所包含的特有信息就越少,其权值[6]可定义为:

其中,Z是对权值标准化,wm>0且
2 时间序列聚类融合算法
算法包括三步:首先,使用NPE对数据集进行维数约简;其次,对降维后的数据进行聚类,产生聚类成员;最后,使用加权投票法进行聚类融合。
聚类融合算法如下:
输入:数据集Data,近邻个数k,嵌入维数d,聚类个数M,聚类成员个数H
输出:聚类结果
(1)使用PCA对数据集进行预处理;
(2)yi←APCATxi,其中,APCA是PCA的转换矩阵;
(3)计算加权矩阵W;
(4)假设ANPE=[a0,a1,…,ad-1],特征值排序后为0≤λ0≤…≤λd-1;
(5)yi=ANPETxi,得到变换后的矩阵Y;
(6)使用K均值聚类将Y聚成M个类,进行H次,得到H个聚类成员;
(7)计算每个聚类成员的权值;
(8)对聚类成员使用加权投票进行聚类融合。
3 实验
3.1 数据集描述
表1列出了来自不同领域的10个时间序列数据集[7]的主要特征。
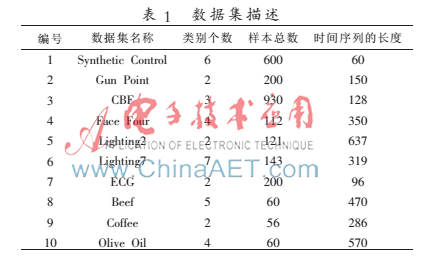
3.2 评价准则
聚类性能用micro-p[6]表示,如式(6)所示。设数据集分为c类{C1,C2,…,Cc},n为样本个数,ah表示实验正确分到Ch中的样本个数,micro-p越大,聚类效果越好。

3.3 性能比较
每一种测试重复10次,记录平均的micro-p,结果如表2所示。第2列是在原始数据上进行K均值聚类的micro-p,第3、4、5列分别是对PCA、PAA以及NPE降维后的数据进行K均值聚类时最高的micro-p以及相应嵌入空间的维数;第6列给出了对NPE降维后的数据进行聚类融合最高的micro-p以及相应聚类成员个数,用NPEC表示聚类融合算法。

对表2中实验结果进行配对样本t检验,结果如表3所示。

从表2、表3可以看到,NPEC的平均micro-p为 0.8,高于其他方法。另外,原始数据、PCA、PAA分别与NPEC配对样本t检验的概率p值都小于0.05,说明NPEC的聚类性能显著地好于这三种方法。
3.4 参数对算法性能的影响
图1为在Coffee上,将k固定为10,micro-p随d的变化情况。当d较小时,micro-p较低,聚类性能较差。产生这种情况,一种可能的解释为数据集中不同的样本经过NPE映射以后,在低维空间重叠在了一起。随着d增加,micro-p快速上升,说明本文提出的算法并不需要很高的嵌入维数就可以获得不错的聚类效果。

图2为在Synthetic Control上,将d固定为43, micro-p随k的变化情况。随着k的增加,micro-p在一定范围内波动,说明k对聚类性能的影响较小。

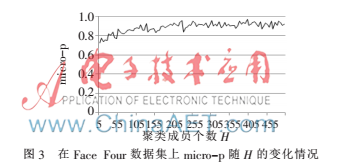
图3给出在Face Four上,micro-p随H的变化情况。当H从5增长到100时,micro-p逐渐提高,当H继续增大时,micro-p保持稳定并在一定范围内波动。
4 结论
本文提出了一种基于NPE的时间序列聚类融合算法,与已有方法PCA、PAA相比,这种方法更能提高聚类性能。在算法中,如何选择最优的嵌入维数以及共识函数的设计,值得今后进一步研究。
参考文献
[1] 陈龙威,孙旭飞.一种基于时间序列分层匹配的骑线车辆检测方法[J].微型机与应用,2014,33(21):88-91.
[2] 苏木亚,郭崇慧.基于主成分分析的单变量时间序列聚类方法[J].运筹与管理,2011(6):66-72.
[3] 李海林,郭崇慧,杨丽彬.基于分段聚合时间弯曲距离的时间序列挖掘[J].山东大学学报,2011,41(5):57-62.
[4] He Xiaofei, Cai Deng, Yan Shuicheng, et al. Neighborhood preserving embedding[C]. IEEE International Conference on Computer Vision, 2005:1208-1213.
[5] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500):2323-2326.
[6] 唐伟,周志华.基于Bagging的选择性聚类集成[J].软件学报,2005,16(4):496-502.
[7] Chen Yanping, KEOGH E, et al. The UCR Time Series Classification Archive. www.cs.ucr.edu/~eamonn/time_series_data/.2015.

