摘 要: 对比分析了最小半径泊车算法和不等半径泊车算法的基本原理,分析了汽车在低速情况下泊车入库时的后轮轨迹特点。同时在MATLAB环境下对两种算法进行了仿真研究,并且对仿真数据进行了比较分析。结果表明,不等半径泊车算法对泊车起始位置要求相对较低,更符合实际操作需求。
0 引言
自动泊车系统是一种智能汽车安全辅助系统,是一种全新的智能驾驶技术,它能够使汽车驾驶员在复杂的城市环境内快速便捷地完成泊车任务,降低了因泊车空间狭小或驾驶技术不熟练而引发交通事故的概率,对于当前汽车工程领域的研发具有重要意义[1-2]。
近几年,国内外很多学者对自动泊车系统进行了相关研究。法国国立计算机及自动化研究院Paromtchik等人研究了泊车运动轨迹方面的工作[3],台湾成功大学Chao等人通过全景摄像头获取模型小车相对于车位之间的位置并生成可行的参考泊车路径[3],德国艾尔默斯公司(Elmos)宣布推出可用于驱动超声波传感器的E524.02和E524.03数字超声波倒车辅助系统系列芯片[4],其中浙江大学开展的相关研究是该领域的优秀代表。浙江大学周泓、王文飞对实现自动泊车系统涉及到的3个核心算法进行了探索和研究[5],根据泊车位空间信息,通过泊车路径算法计算出一条最简单泊车的行车路径,但是并没有将该算法与不等半径泊车算法进行对比,没有对泊车起始位置的误差进行数据分析。本文针对泊车起始位置的选择,以泊车路径规划为依据,对比分析了最简单泊车算法和不等半径泊车算法的基本原理,通过仿真数据分析,总结出两种泊车算法对汽车起始位置的约束范围。
1 模型建立与算法分析
1.1 运动学模型的建立
正常情况下,汽车倒车过程可以认为是低速保持不变的过程[6],在这种情况下车轮不会发生侧滑,可以认为车后轮垂直方向速度为0,其方程式为:

根据图1车辆运动学模型[7]可知,汽车前、后轴中心点位置关系有:


对式(2)进行微分,得到其速度关系表达式:

由此将式(5)代入式(4),即可求得车辆回转圆角速度为:

将式(5)、(6)代入式(3)得到后轴线中心点在x、y方向上的速度为:

然后将式(6)对时间积分,最后代入式(7)后,再对时间微分,即可得到后轮轴线中心点轨迹方程:
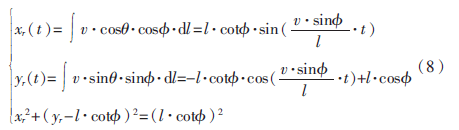
1.2 泊车算法分析
1.2.1 最简单泊车算法
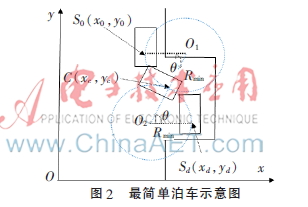
由图2最简单泊车示意图可知,车辆泊车轨迹是由两段相切的圆弧组合而成的S形曲线。最简单泊车过程中,汽车始终以最小转弯半径运动。汽车首先往停车位方向将方向盘打死,从起始位置S0(x0,y0)到达两段圆弧的切点C,然后再反方向打死方向盘直至到达目标位置Sd(xd,yd)。根据数学理论基础可知,车轮划过的圆弧曲线长度最短,所需的停车位空间最小,汽车可以方便快速地完成泊车任务。
1.2.2 不等半径泊车算法

由于最简单泊车算法对汽车起始位置要求较高,当车辆未能到达标准起始位置时,容易导致泊车过程失败。其失败的主要原因在于汽车两段泊车轨迹均以最小泊车半径运动,起始位置可控范围较小[8]。由图3不等半径泊车示意图可知,如果将第一段泊车轨迹改为不等半径运动,那么对于汽车起始位置的要求会大大降低,整个泊车过程更加简单方便。
2 仿真结果分析
本文根据运动学模型建立MATLAB仿真[9],由汽车后轮轴中心点轨迹方程进行仿真,其结果如图4所示。

由轨迹方程和图4汽车后轮轨迹图容易得知,汽车车轮始终在做等半径同心圆运动,车后轮轨迹与汽车轴距和车身转向角有关,而与汽车行驶速度无关,由此可以得出,汽车泊车过程实际是汽车车轮反复画圆弧的过程。基于该理论基础,下面对泊车过程轨迹进行仿真分析。

通过建立笛卡尔坐标系,对汽车车身各点坐标进行准确的定位,从而对泊车过程中的泊车轨迹进行仿真,最简单泊车、不等半径泊车轨迹图分别如图5、图6所示。由仿真图可知,虽然不等半径泊车算法的第一段泊车半径明显大于汽车最小转弯半径,而且汽车所需的停车位长度也明显增加,但是其对于汽车起始位置的可控范围明显增大。
不同的汽车驾驶员具有不同的驾驶习惯和驾驶技能,在实际操作中,无法保证每一个驾驶员都能准确到达标准的起始位置。出于以上情况的考虑,下面将从起始位置的变化范围对两种算法进行仿真数据分析和比较。
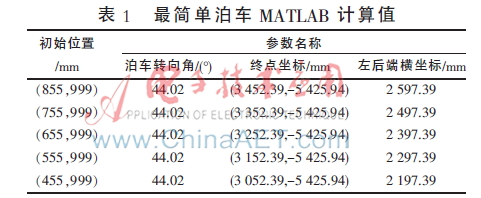
通过表1第1组数据的汽车后轴中心点坐标易求得泊车空间右墙面顶点坐标为(4 407.39,-6 524.94),据数据统计,普通停车位的大小为2.2 m×7.5 m[10-11],由此可确定最简单泊车算法的横向坐标变化范围为2 207 mm~4 407 mm。同时,由图7和表1第5组数据容易得到当汽车起始位置为(455,999)时,汽车左下端横坐标为 2 197.39,小于最简单泊车横坐标变化范围的最小值,此时,汽车车身超出停车位空间,最简单泊车方案失败。在这种情况下,汽车后轴中心点的横向位置变化范围不足400 mm,这对于驾驶员对起始位置的控制有着很高的要求,缺乏一定的灵活性。
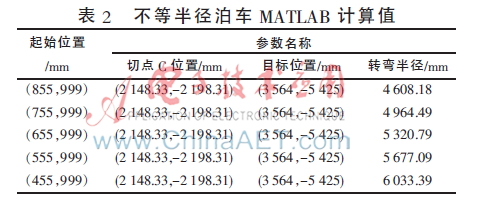
根据表2数据分析可知,随着汽车起始位置的改变,第一段泊车半径也逐渐增大,且大于汽车最小转弯半径。另外,由图8和表2第5组数据可知,当起始位置为(455,999)时,第一段泊车半径为6 888.39 mm,小车成功到达目标位置,顺利完成泊车过程,相比最简单泊车的横向位置变化范围,该算法更加灵活方便。
对于有效的起始位置,必须保证在泊车过程中不与周围的障碍物发生碰撞。通过数学建模,可以将这一问题简化为两个约束条件[5]:

其中,LBo1为圆心O1到前方障碍物的距离,L为车宽。
由此可以确定横向位置的变化范围:

确定了横向位置的变化范围,再通过横纵坐标的几何关系,同理可以确定纵向位置的变化范围。下面通过改变汽车起始位置和目标位置的坐标,由两个约束条件计算出汽车起始横向位置和纵向位置的变化范围,如表3所示。
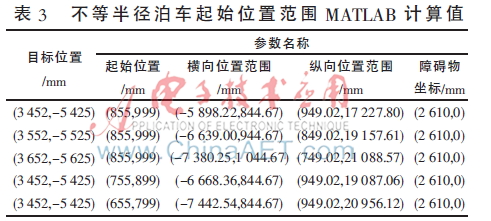
通过表3数据分析可知,不同的起始位置和目标位置所对应的水平横向位移不同。不等半径泊车算法使起始位置的选择不再局限于一点上,更加符合实际的需要,通过该算法使泊车过程更加方便快捷。
3 结论
本文首先通过建立泊车过程的运动学模型,得到车轮运动轨迹表达式,然后通过在MATLAB下的泊车轨迹仿真,验证了最简单泊车和不等半径泊车的可行性,并且将两者进行对比分析仿真,得到不等半径泊车算法对汽车起始位置的要求相比最简单泊车算法更加符合实际需求,对于起始位置的选择更加灵活方便。
参考文献
[1] 禄盛,黄显杭,苏岭,等.自动泊车系统模型研究与实车验证[J].重庆邮电大学学报(自然科学版),2014,26(4):522-529.
[2] Ryu Young-woo, Oh Se-young, Kim Sam-yong. Ro-bust automatic parking without odometry using en-hanced fuzzy logic controller[A]. IEEE International Conference on Fuzzy Systems, Sheraton Vamcouver Wall Centre Hotel, Vancouver, BC, Conda, 2006.
[3] 朴昌浩,禄盛,张艳,等.自动泊车系统设计[M].北京:科学出版社,2014.
[4] 艾尔默斯公司.数字超声波倒车辅助系统[J].微型机与应用,2013,32(10):89.
[5] 周泓,王文飞.自动泊车系统中核心算法的研究[J].电路与系统学报,2012,17(3):71-76.
[6] 杨妮娜,梁华为,王少平.平行泊车的路径规划方法及其仿真研究[J].电子测量技术,2011,34(1):42-45.
[7] 张伟东.基于预瞄点的自动倒车设计和实现[J].轻工机械,2011,29(3):96-100.
[8] 王道斌,梁华为,杨妮娜,等.两种自主泊车路径规划方法的对比研究[J].电子测量技术,2011,34(1):27-31.
[9] 薛年喜.MATLAB在数字信号处理中的应用[M].北京:清华大学出版社,2008.
[10] 罗奕树,张在龙,王日信.自动泊车小车转弯参数及特征环境参数的确定[J].闽江学院学报,2011,32(5):46-50.
[11] Zhao Yanan, EMMANUEL G. Collins Jr.. Robust automatic parallel parking in tight spaces via fuzzy logic[J].Robotics and Autonomous Systems, 2005(51):111-127.

