摘 要: 针对传统优化算法在图像聚类分析中存在的复杂度高、容易陷入局部最优解的问题,提出了使用猫群算法求解图像聚类问题。该算法通过分组和混合策略的机制进行信息传递,用猫记忆当前群体中的全局最优解来更新自身,提高了算法的搜索能力;阐述了猫群算法的搜寻模式和跟踪模式,讨论了两种模式下猫群的速度、位置更新公式;并说明了利用该算法求解图像聚类分析问题的具体步骤。通过实验验证了猫群算法在图像聚类分析中的有效性和准确性。
0 引言
图像的聚类分析就是在错误率最小的情况下,把特征相近或者相同的图像归为一类,是模式识别研究方向的一个重要环节。人们已经找到了许多用于图像聚类分析的群体仿生智能优化算法,其中比较典型的算法包括粒子群算法、遗传算法以及蚁群算法等。粒子群算法在后期不能很好地跳出局部最优;遗传算法搜索速度比较缓慢,不能较好地进行局部搜索;蚁群算法需要强调信息素的作用,增加了算法的时间复杂度,降低了分类效率。为了解决上述问题,本文提出了解决图像聚类分析的一种智能仿生算法——猫群算法,并以图像中不同物体聚类分析为例,介绍该算法解决聚类问题的实现方法并验证算法的正确性和有效性。
1 猫群算法的基本原理
猫群算法是通过观察猫在日常生活中的行为动作提出的群体智能仿生算法,猫即为待求优化问题的可行解[1]。该算法将猫的行为分为搜寻模式和跟踪模式,在搜寻模式中猫处于休息、张望的状态;而在跟踪模式中猫在跟踪动态目标。在整个猫群中,绝大多数猫执行搜寻模式,而只有少量的猫处于跟踪模式[2]。在搜寻模式下,记忆池记录了猫所搜寻的邻域位置点,记忆池的大小代表猫能够搜索的地点数量,通过变异算子,改变原值,使记忆池存储了猫在自身的邻域内能够搜索的新地点,猫根据保存在记忆池中适应度值的大小选择一个最好的位置点。在跟踪模式下,每一次迭代中,猫将跟踪一个“极值”来更新自己,这个“极值”是目前整个种群找到的最优解[3],使得猫的移动方向向着全局最优解逼近,利用全局最优的位置来更新猫的位置,具有向“他人”学习的机制。然后混合成为一个群体,根据分组率,随机地将猫群分为搜寻模式和跟踪模式两种模式,直到算法执行完预定的种群进化次数结束。
1.1 搜寻模式
在搜寻模式中,定义了3个基本要素:记忆池、个体上每个基因改变范围、个体上需要改变的基因的个数。记忆池中记录了猫所搜寻的邻域位置点,猫从中选择一个适应度最好的位置点;在算法开始之前设定个体上每个基因改变范围的值,一般取值为0.2;在基因总长度的范围内随机挑选一个值作为个体上需要改变的基因个数。搜寻模式可分为如下3个步骤:
(1)复制自身位置。猫把自身的位置复制J份并且存放在记忆池中,J为记忆池的大小[4]。
(2)执行变异算子。变异算子是一种局部搜索操作,每只猫经过复制、变异产生邻域候选解,在邻域里找出最优解,即完成了变异算子。对记忆池中的每个个体,个体上每个基因改变的范围是一个随机值,它的大小取值范围是从零至个体上基因总长度之间,并且是在算法开始之前设定的。根据个体上需要改变的基因的个数和改变的范围,在原来的位置上随机加上一个扰动,然后使用新的位置来替代原来的位置[1]。
(3)执行选择算子。复制猫的自身位置,把新的位置副本保存在记忆池中,从中选择适应度值最高的新位置来代替当前猫的位置。
1.2 跟踪模式
猫进入跟踪模式后,猫群算法即类似于粒子群算法,采用速度-位移模式来移动每一位基因的值。猫的跟踪模式可以通过以下两步来描述。
(1)速度-位移模型操作算子
整个猫群经历的最好位置,即为目前得到的最优解[1],记做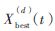 。每个猫都有一个速度,记做Vi={vi1,vi2,…,viL},定义式(1):
。每个猫都有一个速度,记做Vi={vi1,vi2,…,viL},定义式(1):
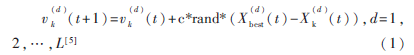
其中,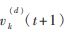 表示更新后第k只猫的第d位基因的速度值,L为个体上基因的总长度[1];
表示更新后第k只猫的第d位基因的速度值,L为个体上基因的总长度[1]; 代表的是第k只猫Xk(t)所处位置的第d个分量;c是一个常量,其值需要根据不同的问题而定;rand是一个随机数,它的取值范围是0~1。
代表的是第k只猫Xk(t)所处位置的第d个分量;c是一个常量,其值需要根据不同的问题而定;rand是一个随机数,它的取值范围是0~1。
(2)根据式(2)更新第k只猫的位置:
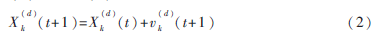
其中, 代表位置更新后第k只猫Xk(t+1)的第d个位置分量。
代表位置更新后第k只猫Xk(t+1)的第d个位置分量。
2 控制参数选择
2.1 群体规模
较大的群体规模可以增大搜索的空间,使所求的解更逼近于最优解,但增加了算法的时间和空间的复杂度,较小的群体规模容易陷入局部最优。
2.2 分组率
分组率就是为了使猫群算法更加逼近真实世界猫的行为而设定的一个参数,该参数一般取一个很小的值,使少量的猫处于跟踪模式,保证大部分猫处于搜寻模式。
2.3 个体上每个基因改变范围
进行基因的改变主要是为了增加解的多样性。个体上基因的改变范围太小很难产生新解,太大则会使得算法变成随机搜索。
2.4 最大进化次数
进化次数过少,使算法还没有取得最优解提前结束,出现“早熟”现象;进化次数过多,算法早已收敛到了最优解,增加了算法的运算时间。
3 基于猫群算法图像聚类分析设计
一幅图像中含有多个物体,在图像中进行聚类分析需要对不同的物体分割标识[6],如图1所示。有A、B、C、D、B、C、D、A、C、D、A、B共12个待分类样品,如何将这12个物体分成4类呢?本文介绍用猫群算法解决图像中不同聚类问题的实现方法。
3.1 构造个体

图1中有12个物体需要进行聚类,假设得到的一种结果如图2所示,样品的分类号位于每个样品的下方;样品的编号在右上角且固定不变[7],并且编号不同。
猫群使用符号编码,位串长度L=12,样品所属的类号取值范围为1~4。因为样品的编号是固定的,所以某个样品在每个解的位置是固定的,而样品所属的类别随时保持编号变化。如果编号为n,则代表第n个样品,而第n个位所指向的值代表第n个样品的归属类号[7]。
为了算法求解方便,设定A用数字1表示,B用数字2表示,C用数字3表示,D用数字4表示。设初始解的编码为(1,3,2,1,4,3,2,4,3,2,4,1),如表1所示。这个解并不是最优解,而是一种假设分类情况。

表1表示第1、4、12号样品被归类到第1类;第2、6、9号样品被归类到第3类;第3、7、10号样品被归类到第2类;第5、8、11号样品被归类到第4类。
3.2 计算适应度
系统初始化了N只猫,算法中取分组率为0.02,根据分组率将猫分为搜寻模式和跟踪模式下的猫,每一只猫的位置就是所求问题的解但不一定是最优解。
(1)将猫的编码表示法转化为类中心表示法
设模式样品集为X={Xi,i=1,2,…,n},其中Xi为D维模式向量,聚类问题就是要找到一个划分C={C1,C2,…,Ck},使得总的类内离散度之和达到最小[5]。定义式(3):

其中,Cj为第j个聚类的中心,d(Xi,Cj)为样品到对应聚类中心的距离,聚类准则函数Jc即为各类样品到对应聚类中心距离的总和[8]。
确定聚类中心后,可由最邻近法则确定聚类的划分。即对样品Xi,若第j类的聚类中心Cj满足式(4)时,则Xi属于类j。
d(Xi,Cj)=mind(Xi,Cl),l=1,2,…,k(4)
利用猫群算法求解聚类问题中,解集(即猫群)由每一个可行解(猫)组成。本文采用基于聚类中心集合作为猫的对应解[9],每一只猫的位置由k个聚类中心组成(k为已知的聚类数目)。
在一个具有k个聚类中心、样品向量维数为D的聚类问题中,猫的结构可以由位置、速度和适应值[1]来表示:
Cat(i)={location[],velocity[],fitness}
其中猫的位置通过Cat(i).location[]=[C1,…,Cj,…,Ck]表示,Cj表示第j类的聚类中心,是一个D维矢量。猫的速度可以表示为:Cat(i).velocity[]=[V1,…,Vj,…,Vk];Vj表示第j个聚类中心的速度值,Vj也是一个D维矢量。
(2)计算适应度
猫的适应度值使用Cat.fitness来表示并且采用以下方法计算。
①按照最邻近法则式(4),确定该猫的聚类划分。
②重新计算聚类中心,按照式(3)计算总的类内离散度Jc。
③使用公式Cat.fitness=1/Jc表示猫的适应度,Jc是总的类内离散度和。猫所代表的聚类划分的总类间离散度越小,猫的适应度越大。
3.3 位置更新
(1)跟踪模式
在迭代过程中,用C_gd表示猫群经历的最优位置和适应度,记忆猫群的全局最优解。C_gd={location[],fitness},根据式(1)和式(2)可以得到猫的速度公式如式(5)所示,位置更新公式如式(6)所示。
Cat(i).velocity(j).feature=Cat(i).velocity(j).feature+c*rand(Nwidth,Nwidth)*(C_gd.location(j).feature-Cat(i).location(j).feature)(5)
Cat(i).location(j).feature=Cat(i).locaiton(j).feature+Cat(i).velocity(j).feature(6)
其中,C为一个定值,根据经验一般取c=2会有比较好的效果。
(2)搜寻模式
猫复制自身副本,在自身邻域内加一个随机扰动到达新的位置,再根据适应度函数求取适应度最高的点作为猫所要移动到的位置点。其副本的位置更新函数如下:
current_Cat(n).location(k).feature=current_Cat(n).location(k).feature+current_Cat(n).location(k).feature*(SRD*(rand*2-1))(6)
其中,SRD=0.2,即每个猫个体上的基因值变化范围控制在0.2之内,相当于在自身邻域内搜索。
3.4 实现步骤
(1)设置相关参数。设定算法参数(分组率为0.02,基因变化范围为[-0.2,0.2],记忆池大小SMP=5),输入最大迭代次数(MaxIter)和类中心数(centerNum)。
(2)猫群的初始化。对于第i只猫Cat(i),为每一个样品随机指派某一类作为最初的聚类划分,并计算各个类的聚类中心,把它作为猫i的位置编码Cat(i).location[][1],计算猫的适应度Cat(i).fitness,反复进行,生成CatNum个猫。
(3)根据分组率随机设定猫群中执行搜寻模式的猫和跟踪模式的猫,即将猫的模式标识位作出相应的改变,在搜寻模式下猫的模式标识位为0,在跟踪模式下猫的模式标识位为1。
(4)在跟踪模式下,猫需要记住一个猫群的全局最优位置C_gd.location(j),对于每一只猫,根据式(5)和式(6)更新猫的速度和位置,这样在执行跟踪模式下的猫总是向着最优解的方向趋近。
(5)在搜寻模式下,对于每一只猫复制5份,并对这5份副本应用变异算子,根据式(6)对它们进行位置改变。将每个聚类中心位置进行变异,计算位置更新后的副本的适应度值,选取适应度最高的点来代替当前位置。
(6)对于每一个样品来说,按照如下步骤来更新适应度值:首先确定猫的聚类中心编码,然后根据最邻近法则确定样品的聚类划分,最后根据相应的聚类划分重新计算新的聚类中心,更新每一只猫的适应度值。
(7)计算所有猫的适应度值,找到当前的最优解。
(8)如果达到结束条件,则算法结束,输出全局最优解;否则回到步骤(3)继续执行。
4 图像聚类分析实验及性能分析
4.1 图像聚类分析实验
本文在Intel(R)Core(TM)i3-2330M处理器、内存为2 GB的计算机上使用MATLAB软件进行了相应的实验,采用欧式距离,设定类中心数为4,最大迭代数为8,最后得到的最优解编码如表2所示。通过样品值与基因值对照比较,发现相同的数据被归为同一类,而且全部正确,最优解出现在第4代。

4.2 算法性能分析
在同样的实验条件下,使用猫群算法、蚁群算法、遗传算法分别对50个不同图像进行聚类分析。3种算法的初始的最大迭代次数都为30,初始候选解个数都为50。3种算法的相关参数选择如下:
猫群算法:初始化50只猫,分组率为0.1,变化域为0.2,记忆池大小为5。
遗传算法:染色体的初始值设为50,给定分类中心M,选择算子采用赌轮选择方法,当交叉算子为0.6、变异算子为0.05时产生下一代。
蚁群算法:初始化50只蚂蚁,信息素蒸发参数为0.9,转换规则参数为0.5。

使用3种算法对50组图像进行10次实验,统计平均最优解出现代数(如图3所示)和平均准确率(如图4所示)。
从图3和图4可以看出,使用猫群算法在收敛速度和算法性能上要优于后两者,并且达到了预期分类效果。
5 结论
猫群算法具有良好的局部搜索和全局搜索能力,算法控制参数较少,通过搜索模式和追踪模式的相互结合,大大提高了搜索优良解的可能性和搜索效率,较其他算法容易实现,收敛速度快,具有较高的运算速度,易于与其他算法结合。该算法主要通过迭代过程来不断地寻找当前最优解,在每一次迭代过程中猫所执行的模式是随机的,在一定程度上提高了算法的全局搜索能力。实验表明,猫群算法在图像聚类问题中比蚁群算法和遗传算法更有效、更加准确。猫群算法目前主要应用于函数优化、图像分类等领域中,具有很好的理论探讨空间和广阔的应用前景。
参考文献
[1] 王光彪,杨淑莹,冯帆,等.基于猫群算法的图像分类研究[J].天津理工大学学报,2011,27(5):35-39.
[2] 范凯波.基于几何特征的车辆目标分类研究[D].天津:天津理工大学,2011.
[3] 王媛妮.顺序形态边缘检测及分水岭图像分割研究[D].武汉:武汉大学,2010.
[4] 吴伟林,周永华.基于差分演化与猫群算法融合的群体智能算法[J].计算机技术与自动化,2014,33(12):78-83.
[5] 陈彬,骆鲁秦,王岩.基于粒子群聚类算法的雷达信号分选[J].航天电子对抗,2009,24(5):25-28.
[6] 张忠华,杨淑莹.基于遗传算法的聚类设计[R].南宁:中国高科技产业化研究会信号处理产业化分会,2008.
[7] 张忠华,杨淑莹.基于遗传算法的图像聚类设计[J].测控技术,2010,29(2):44-46.
[8] 陈建成,屠昂燕.基于粒子群算法的织物组织结构识别[J].湖北第二师范学院学报,2010,27(2):15-16.
[9] 朱燕飞,胡夏云,唐雄民.基于群算法的过程参量聚类研究[J].计算机工程与应用,2012,48(26):36-38.

