摘  要： 针对传统的机器学习算法对不平衡数据集的少类分类准确率不高的问题，基于支持向量机和模糊聚类，提出一种不平衡数据加权集成学习算法。首先提出加权支持向量机模型（Weighted Support Vector Machine，WSVM），该模型根据不同类别数据所占比例的不同，为各类别分配不同的权重，然后将WSVM与模糊聚类结合提出一种新的集成学习算法。将本文提出的算法应用于人造数据集和UCI数据集实验中，实验结果表明，所提出的算法能够有效地解决不平衡数据的分类问题，具有更好的分类性能。

　　关键词： 不平衡数据集；权值；支持向量机；聚类；集成

0 引言

　　不平衡数据[1-2]分类问题一直备受关注，已成为机器学习领域中的研究热点。现实生活中，存在着许多不平衡数据的例子。如：医疗诊断、故障检测等。目前，不平衡数据分类问题的处理方法主要分为两类：

　　数据层面上，主要是对原始数据集进行处理，利用少数类过采样、多数类欠采样等方法使原始数据集各类别数据个数达到相对平衡。过采样技术（Synthetic Minority Ove-rsampling Technique，SMOTE）[3]通过少类样本和其近邻样本的线性关系获得新的少类样本，减少了过拟合现象，但在生成新样本时存在盲目性，容易出现样本混叠现象，增加噪音样本。单边选择欠采样技术（One-sided Selection）[4]寻找互为最近邻的异类样本对，并将其中的多类样本判断为噪声点并删除，但将噪声点完全删除，会丢失重要的数据信息。

　　算法层面上，主要是对已有分类算法进行改进或是设计新算法。赵相彬等人提出基于欠采样与修正核函数相结合的SVM算法[5]，根据保角变换修正SVM的核函数，有效地提高了分类准确率。Seref等人提出Weighted Relaxed Support Vector Machine（WRSVM）[6]，WRSVM是代价敏感学习和Relaxed SVM（RSVM）的结合，减少了离群点的影响。Lin等人提出基于SVM和聚类的不平衡数据分类算法[7]，该算法利用模糊聚类（FCM）将训练集的多类数据集分成几个子集，然后用每个子集和训练集的少类分别训练子分类器，最后通过投票原则确定最终分类结果。但FCM并不是对数据集平均分组。例如，设多类数据个数为100个，少类数据个数为30个，则需将100个多类数据分为3个子集，各子集个数可能为（24，36，40）、（10，25，65），当子集个数为65时，和少类数据个数30相比，两类数据个数依然是不平衡的。

　　因此，针对这一问题，本文提出一种加权集成学习算法——Ensemble Weighted Sup-port Vector Machine based on FCM（FCM-EN WSVM）。首先提出加权支持向量机模型，该模型根据不同类别数据所占比例不同，为各类别分配不同的权重。然后利用FCM将训练集的多类数据分为若干子集，每个子集分别和训练集的少类作为新的训练集训练多个WSVM分类器，最后对测试集进行测试，通过投票原则确定最终分类结果。新算法有效地解决了不平衡数据的分类问题。

1 支持向量机

　　支持向量机（Support Vector Machine，SVM）[8-9]是Corinna Cortes和Vapnik等人于1995年首先提出的，其基本原理：假设给定带有标签的训练集S={（x1，y1），…，（xn，yn）}，其中，xi∈RN表示样本点，yi∈{-1，1}表示所属类别标签，i=1，…，n。则SVM模型的目标函数为：

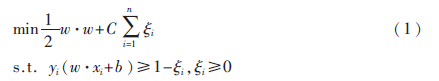
　　其中?孜i为松弛变量，C为惩罚参数，建立拉格朗日函数，式（1）转化为其对偶问题：

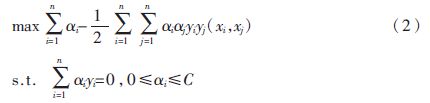
　　则其决策函数为：

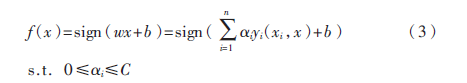
　　在非线性可分情况下，输入样本空间找不到最优分类超平面，因此将数据通过核函数映射到高维特征空间中，此时：

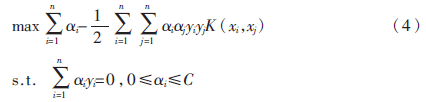
　　其决策函数为：

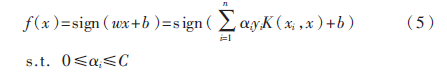
　　2 本文提出的算法

　　2.1 加权支持向量机（WSVM）

　　为了减小数据类别不平衡对SVM训练模型的影响，根据每个类别数据对分类贡献的不同，区别对待每一类别数据，为其分配不同的权值，则WSVM模型的目标函数为：

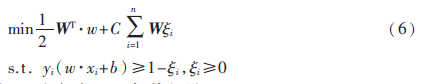
　　其中W为各类别的权值矩阵。

　　式（6）的对偶问题为:

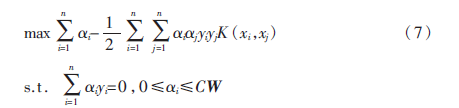
　　那么，映射到高维空间的决策函数为：

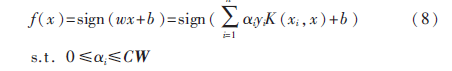
　　2.2 权值的定义

　　权值W需满足以下条件：

　　（1）少类数据的权值大于多类数据的权值，即Wshao>Wduo；

　　（2）Wi∈（0，1），且，C为数据的类别数。

　　设训练集的样本数为N，类别数为C，各类别的样本数从小到大排序依次为n1，n2，…，nC，则第i类数据的权值定义为：

　　根据不同类别样本个数所占的比例为其分配不同的权重，多类数据的权重大，少类数据的权重小，从而使各类别数据比例趋于平衡。

　　2.3 FCM-ENWSVM

　　模糊C均值聚类算法（Fuzzy C-means，FCM）[10]于1981年被Bezdek提出。它的思想是将数据集划分为不同的簇，要求同一簇的对象之间的相似度尽可能的大，而不同簇的对象之间的相似度尽可能的小。

　　FCM-ENWSVM算法（基于支持向量机和聚类的不平衡数据加权集成学习算法）：

　　（1）计算训练集的多类数据和少类数据的个数，并将其个数比记为M；

　　（2）利用FCM算法将多类数据集分为M个子集；

　　（3）M个子集分别和少类数据构成新的训练集，训练M个WSVM分类器；

　　（4）分别用M个分类器对测试集进行测试。

　　最终结果通过投票原则决定。

3 实验结果及分析

　　3.1 人造数据

　　随机生成一个300×2的数据集，按3∶1的比例随机分为训练集和测试集。实验中，分别用训练集训练SVM、WSVM两种分类器，核函数选择文献[11]中的Linear、RBF。图1、图2分别表示两种核函数的条件下，两种分类器对测试集的测试结果，其中每幅图中Original表示测试集真实的类别分布，SVM、WSVM表示用SVM、WSVM两种分类器分类后的测试集类别分布，加号表示正类（少类）1，点表示负类（多类）0，圈表示错分的数据点F。

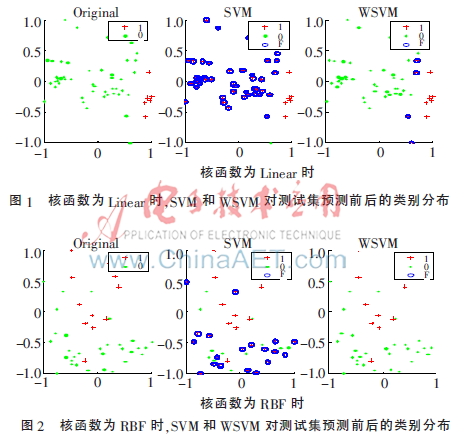
　　从图1、图2可以看出，在两种核函数下，WSVM的分类正确数都明显高于SVM的。WSVM考虑了不同类别数对分类准确率的贡献多少，权值起到了平衡的作用，有效地提高了分类器的性能。

　　3.2 UCI数据实验

　　从UCI数据库中选取了6个数据集，分别为wine、glass、housing、pima、breast、bupa，各数据集的基本信息如表1所示。

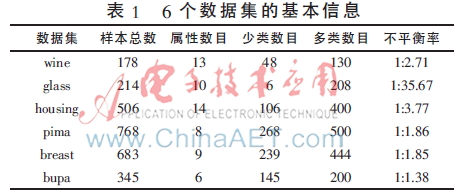
　　实验中，将表1中的数据集按3∶1的比例随机分为训练集和测试集，分类方法选择SVM、FSVM[12]、RSVM[11]、FCM-SVM[7]、FCM-ENWSVM（本文算法），评价准则选择文献[13]中的G-means、F-measure[13]。为了充分验证本文算法的有效性，图3、图4分别为glass、wine数据的训练集打乱顺序进行8次实验的结果折线图，表2~表5为其他4个数据集的实验结果，均取循环20次的平均值。

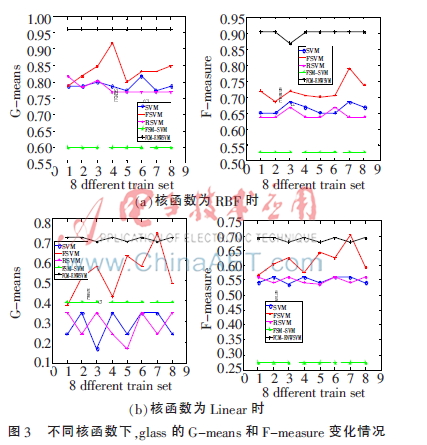
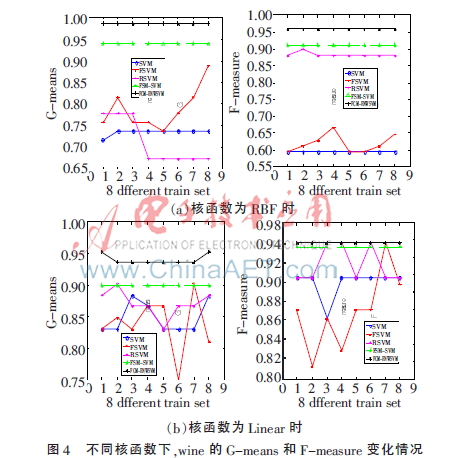
　　从图3、图4可以看出，本文提出的算法FCM-ENWSVM的G-means和F-measure明显高于其他方法。FCM-ENWSVM的变化比较稳定，而SVM、FSVM、RSVM的变化较大，FCM-SVM虽然比较稳定，但是准确率低，没有考虑到FCM不是对数据集进行平均分组，训练集的多类、少类个数依然是不平衡的。然而，FCM-ENWSVM改进了这些算法的不足之处，通过FCM和权值改善了数据的不平衡性，具有更好的分类效果。

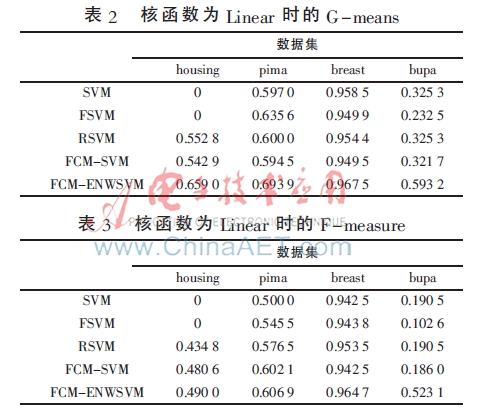
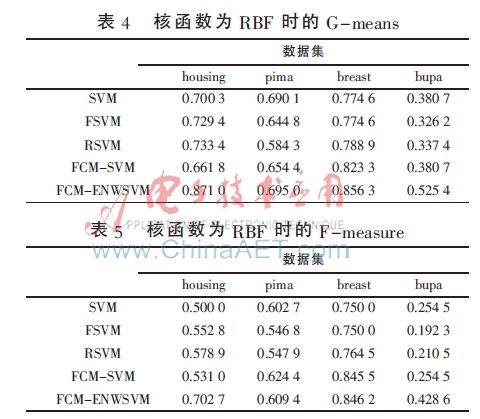
　　从表2~表5中可以看出，在不同的核函数下，FCM-ENWSVM的G-means、F-measure都高于其他方法。特别地，对于housing数据，当核函数为Linear时，SVM、FSVM的G-means、F-measure都为0，而FCM-ENWSVM的准确率相对较高。还可以发现，当多类少类的不平衡性差时，如bupa数据，SVM和FCM-SVM的结果相同，说明在FCM-SVM中，FCM并没有起到作用，准确率依然不高，而FCM-ENWSVM的却相对较高。FCM-ENWSVM利用了FCM算法，并考虑到用权值来改善数据的类别不平衡度，从而解决了FCM不平均分组再次造成数据不平衡的问题，有效地提高了分类准确率。

4 结论

　　本文针对传统分类算法对不平衡数据的分类准确率低的问题，基于支持向量机和模糊聚类，提出了一种不平衡数据加权集成学习算法。该算法根据不同类别样本对分类贡献的不同为每个类别分配不同的权重，提出加权支持向量机模型，并且利用模糊聚类算法对训练集的多类数据进行聚类，聚类后的每个子集分别和训练集的少类数据作为训练集，训练加权支持向量机子分类器。最后通过投票原则决定最终分类结果。将新算法应用于实例数据集的分类问题中，有效性和优越性得到了证明。

参考文献

　　[1] JAPKOW I， STEPHEN S. The class imbalance problem： a systermatic studay[J]. Intelligent Data Analysis Journal，2002，6（5）：429-450.

　　[2] YANG Q，WU X. 10 challenging problems in data mining research[J]. International Journal of Info-rmation Technology&Decision Making，2006， 5（4）： 597-604.

　　[3] CHAWLA N V， BOWYER K W， HALL L O， et al. SMOTE： synthetic minority over-sampling Technique[J]. Journal of Artificial Intelligence Resaerch， 2002（16）：321-357.

　　[4] KUBAT M， MATWIN S. Addressing the curse of  imbalanced training sets： one-sided selection[C]. Proceedings of the 14th International Conference on Machine Learning， San Francisco， 1997：179-186.

　　[5] 赵相彬，梁永全，陈雪.基于支持向机的不平衡数据分类研究[J].计算机与数字工程，2013，41（2）：241-243.

　　[6] SEREF O， RAZZAGHI T， XANTHOPOULOS P. Weighted relaxed support vector machines[J]. Annals of Opearations Research，Springer US，2014（9）：1-37.

　　[7] Lin Kaibiao， Weng Wei， ROBERT K， et al. Imbalance data classification algorithm based on SVM and clustering function[C]. The 9th International Conference on Computer Science & Education， 2014：544-548.

　　[8] CORTES C， VAPNIK V. Support-vector networks[J]. Machine Learning，1995，20（3）：237-297.

　　[9] VAPNIK V.Statistical learning theory[M]. New York： J.Wiley，1998.

　　[10] BEZDEK J. Pattern recognition with fuzzy objec-tive function algorithms[M]. New York： Plenum press，1981.

　　[11] 梁红霞，闫德勤.粗糙支持向量机[J].计算机科学，2009，36（4）：208-210.

　　[12] Huang Hanpang， Liu Yihung. Fuzzy support vector machines for pattern recognition and data mining[J]. International Journal of Fuzzy Systems， 2002，4（3）：826-835.

　　[13] 徐丽丽，闫德勤，高晴.基于聚类欠采样的极端学习机[J].微型机与应用，2015，34（17）：81-84.