摘  要： 岩石薄片显微图像在有较多的平坦背景区域且受到杂质和噪声干扰时，现有的聚焦算法极易出现自动聚焦失败。本文针对岩石薄片显微图像的相关特性，提出一种改进的Vollath函数清晰评价函数，该算法基于图像的互相关函数，可以有效抑制噪声、减少杂质干扰，再结合变步距渐进爬山算法实现岩石薄片显微图像的自动聚焦。大量实验表明，该算法基本可以满足实时性要求，并表现出卓越的单峰性和抗噪性，已在岩石薄片显微图像的自动聚集中进行实际应用。

　　关键词： 自动聚焦；噪声；杂质干扰；Vollath函数；爬山算法

0 引言

　　岩石薄片图像采集是长久保存薄片信息的一种有效手段，也是薄片图像分析的基础。通过光学显微镜成像时，一次成像只能表现薄片的某一个局部，例如常用的10倍物镜，采集完整张薄片需要大约150个视域的图像。因此，要将全薄片图像采集并保存，有效的方法是计算机控制视域转换、自动采集，再将各视域图像进行拼接。在自动采集的过程中，由于显微镜景深较小，视场切换之后很容易出现图像失焦，因此在每个视域的自动采集过程中都需进行自动聚焦。

　　自动聚焦是指在计算机控制显微镜成像的过程中，通过相应的算法控制电机调节镜头或者载物台获取最清晰的图像，主要有基于测距原理的主动式聚焦和基于图像处理的被动式聚焦[1]两种方式。由于显微图像是在高放大倍数、小孔径的物镜下拍摄的，其景深在微米级别，对机械系统要求较高，主动式聚焦方式存在诸多缺陷，因此多采用基于图像处理方法的被动式聚焦方法。被动式聚焦方法是获取摄像头的实时图像数据帧，分析当前图像的聚焦状态，按照一定的搜索策略控制步进电机调节载物台位置，实时反馈获取最清晰的图像。在这个过程中，最关键的是选择一个合适的判断图像清晰度的评价函数，同时选择合适的清晰度极大值搜索算法控制步进电机调节载物台获取最清晰的图像。

　　岩石薄片显微图像的特点是：个体特征不明显，不同岩性、致密度的岩石薄片差异较大，岩石薄片中杂质干扰较多等。在一般应用中，常见的清晰度评价函数基本能够满足要求，但是岩石薄片存在这样一些局部视域，当表面有较多的平坦背景区域、图像细节不明显而盖玻片上又有杂质时，这种情况会造成清晰度函数曲线出现局部极值，导致自动聚焦失败。特别是当需要自动连续采集序列图，进行全薄片的图像拼接时，若出现自动聚焦失败，轻则拼接图像部分区域模糊，重则会使图像拼接失败，因此需要进行相关研究以解决这一问题。

　　本文针对岩石薄片显微图像的相关特点，对比现有清晰度评价函数的性能，为减少平坦背景区域和图像噪声对清晰度值的影响，采用最大值Vollath函数作为清晰度评价函数，并使用改进的变步距渐进爬山算法作为清晰度极大值搜索算法。Vollath函数仍能满足实时性要求，而且具有更好的抗噪性，聚焦成功率更高，特别是针对本文岩石薄片显微图像，在目标内容较少的情况下，依旧表现出较好的单峰性和灵敏度，有效抑制了噪声和杂质干扰的影响。

1 常用清晰度评价函数分析

　　选择一个合适的图像清晰度评价函数是自动聚焦算法的关键，聚焦图像比离焦图像细节更加清晰，在空间域上表现为梯度值相对较大，在频域上表现为高频分量更加丰富，这是设计清晰度评价函数的基础。一个好的清晰度评价函数应具有单峰性强、抗噪能力强、无偏性好、灵敏度高以及计算速度快等特点。

　　目前，清晰度评价函数主要是基于频率域、空间域和统计特征等方式来设计评价函数[2]。

　　1.1 基于频率域的清晰度评价函数

　　此类评价函数主要是基于傅里叶变换（或者小波变换）[3]。其理论依据是图像清晰度主要由图像中的高频信息决定，因此将图像转换到频率域上，提取其中的高频分量做为评价依据。

　　这种算法的特点是灵敏度高，但需将图像信息从空间域变换到频率域上，因此计算量较大，运行效率较低，无法满足自动聚焦过程的实时性。

　　1.2 基于统计特征的清晰度评价函数

　　此类评价函数最常用的算法是熵函数[4]，根据香农信息理论，熵值较大时，信息量较多，因此，图像的熵值可以衡量图像信息的丰富程度，也可以用于评价图像的清晰度。

　　图像的熵值公式定义如下：

　　式中，Pi是图像x取灰度值i的概率，L为灰度级数。

　　1.3 基于空间域的清晰度评价函数

　　（1）平方梯度函数

　　该函数公式定义如下所示：

　　式中，I（x，y）为图像在点（x，y）的灰度值，聚焦窗口大小为M×N。

　　在图像内容丰富、噪声较小时，上述函数的性能虽各有差异，但基本都能满足岩石薄片显微图像的自动聚焦要求。当自动聚焦受到噪声、灰尘、平坦背景区域较多等外部因素干扰时，需要对算法进行改进，提高算法的稳定性和抗噪性。

2 最大值Vollath函数

　　2.1 图像聚焦处理窗口的选择

　　聚焦处理窗口是指用来获取图像聚焦函数值的图像处理区域，很多学者在进行图像自动聚焦算法研究时，常通过选取特定聚焦区域的方式来减少数据处理量和提高聚焦精度。

　　常见的聚焦处理窗口选择方法有中心取窗法、1D区域法、多点取窗法、非均匀采样算法等[5]，这些方法多根据感兴趣目标按照一定规律分布或者出现在可预期区域的假设来设计，在使用数码相机聚焦的大景深环境下，这些方法基本可以取得满足聚焦要求的效果。但是在显微镜这种小景深环境下，这些方法是无法满足聚焦要求的。在显微镜下，感兴趣目标可能比较稀疏，目标也可能未出现在聚焦处理窗口区域内，加之在深度离焦情况下，图像是一片模糊，因此无法通过上述方法来选择聚焦处理窗口。基于上述原因，本文选取整幅图像作为聚焦处理窗口。

　　2.2Vollath函数的改进

　　相机成像过程中总是会产生噪声，特别是孤立噪声会对总的清晰度值产生很大影响[6]。Vollath函数在图像噪声较多的情况下有很好的表现，因此采用改进的Vollath函数来计算图像的清晰度值。改进的Vollath函数不仅可以抑制噪声，当岩石薄片显微图像的内容比较稀疏且有杂质干扰时，亦表现出卓越的性能。

　　基于自相关的Vollath函数：

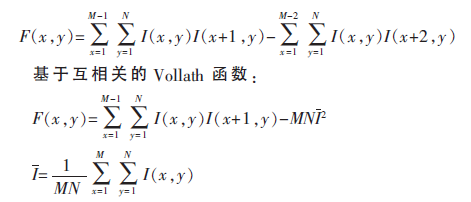
　　式中，I（x，y）为图像在点（x，y）的灰度值，I为图像聚焦窗口内的平均灰度值，聚焦窗口大小为M×N。

　　本文采用基于互相关的Vollath函数作为清晰度评价函数，可将函数等价为：

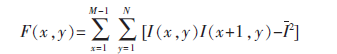
　　为增强评价函数的灵敏性，对Vollath函数进行改进，分别计算像素I（x，y）四邻域内的互相关量。

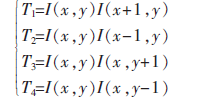
　　得到最大互相关量：

　　Tmax=max（T1，T2，T3，T4）

　　则基于Vollath函数得到的清晰度值为：

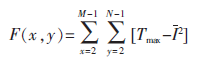
3 自动搜索算法

　　自动聚焦的可靠性和精确度取决于清晰度评价函数，而搜索算法则决定了自动聚焦算法的效率。自动搜索算法即通过控制Z轴方向的电机上下运动，改变显微系统的薄片与镜头之间的距离，寻找清晰度的最大值，从而确认其为图像最清晰的状态。目前比较常见的自动搜索算法有爬山算法、曲线拟合算法、平均搜索算法、斐波那契搜索算法等，其中，爬山算法[7]以其简单、高效、稳定等特性最为常用。本文采用变步距渐进爬山算法[8]，它可以有效避免将局部峰值误判为极大值，提高了偏光显微图像的自动聚焦成功率，该算法步骤如图1所示。

　　（1）设定一个初始位置P0，计算当前清晰度值F（P0）；

　　（2）设定一个初始方向，沿此方向移动一个大步距S1，计算清晰度值F（P1）；

　　（3）比较F（P0）与F（P1），若F（P0）<F（P1），则沿原方向移动并继续计算清晰度值，直到F（Pn-1）>F（Pn）；

　　（4）当F（Pn-1）>F（Pn）时，改变方向移动，此时的步距S2应小于S1（本文中S1为5倍的S2），继续计算清晰度值并作判断，直到找到F（Pn）的最大值停止。

　　在自动搜索聚焦过程中，受机械精度、噪声、薄片灰尘等多种因素的影响，极易出现局部峰值，因此本文加入阈值判断：

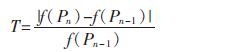
　　若T≤Th，则判定局部峰值，继续搜索；若T>Th，则认为已越过峰值，返回继续搜索，其中Th为判定阈值。本文中的Th根据文献[9]中的实验经验值取0.05为宜。

4 实验结果及分析

　　本文实验在自行设计的多视场自动聚焦、自动采集平台上进行，平台的物镜放大倍率为10倍，相机分辨率为2 592×1 728，自动载物台可进行前、后、左、右各方向的移动，以及上、下聚焦等操作，平台分辨率≤0.625 m，重复定位精度≤5 m，聚焦分辨率≤0.1 m。

　　试验中使用自动采集平台拍摄不同类型的岩石薄片图像，获取从离焦到聚焦再到离焦的序列图，验证算法性能。特别地，采集若干组有较多平坦背景区域且有杂质干扰的显微图像（一般称之为目标内容稀疏），即背景区域较多，岩石颗粒目标比较稀疏的图像），这些图像极易导致自动聚焦失败，通过对这些图像进行实验，可以有效验证算法性能。

　　实验图像如图2所示，其中图2（a）和（b）为无噪声和引入高斯噪声的图像；图2（c）和（d）分别为轻度目标内容稀疏时，聚焦状态和离焦状态的图像，虽然该组图为轻度目标内容稀疏，但也受到薄片杂质干扰；图2（e）和（f）分别为重度目标内容稀疏时，聚焦状态和离焦状态的图像。对这三组图，分别采用平方梯度函数、TenenGrad函数、Brenner函数、熵函数以及本文改进的Vollath函数求取图像清晰度值，并绘制归一化处理的清晰度评价函数曲线，将几种算法和改进的Vollath函数算法进行对比，进而验证本文自动聚焦算法的性能。

　　（1）带噪声图像的算法性能分析

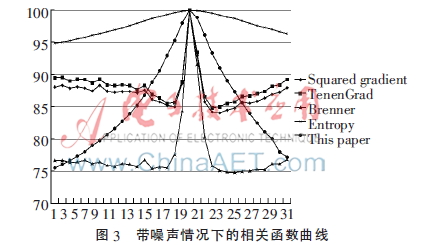
　　模拟数字图像成像过程中会产生噪声，特别是光源较暗、感光元件ISO较高时易产生高斯噪声。在序列图中加入均值为0、方差为0.02的高斯噪声，如图2（a）和（b）对比所示。由图3实验结果所示，熵函数曲线过于平缓，无法进行聚焦。其他函数曲线虽然在轻度离焦时陡峭性、灵敏度保持得很好，但是当处于重度离焦时，TenenGrad函数、Brenner函数受噪声影响很大，而本文的改进Vollath函数则表现出优良的抗噪性。

　　（2）轻度目标内容稀疏情况下的算法性能分析

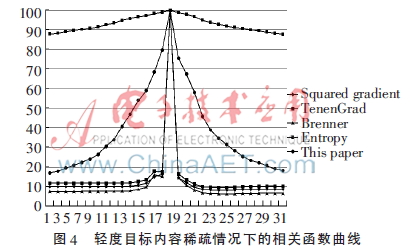
　　如图4实验结果所示，当岩石薄片显微图像属于轻度目标内容稀疏时，除熵函数外的多数算法基本可满足对清晰度评价函数的要求。但观察图4细节部分，TenenGrad函数和Brenner算法出现了一个局部峰值，本文算法相对而言波峰较宽，但依旧保持陡峭性，可实现重度离焦情况下的聚焦。

　　（3）重度目标内容稀疏情况下的算法性能分析

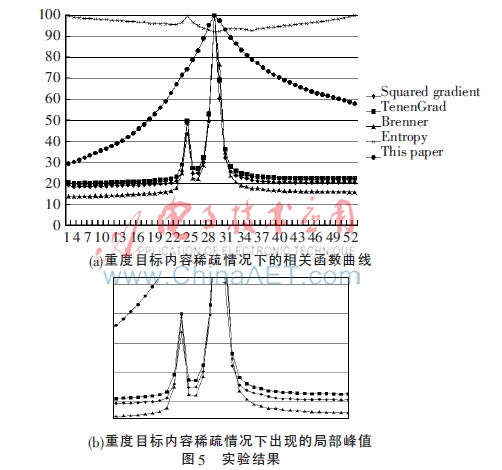
　　在显微镜自动聚焦的应用实践中发现，当显微镜视场处于平坦背景区域较多的情况下，受薄片表面杂质的影响，传统算法极易出现聚焦失败的情况。如图5（b）实验结果所示，受薄片表面杂质干扰时，其他函数曲线出现十分严重的局部峰值形成了双峰，而正是这种原因造成传统算法的聚焦失败。本文算法基于图像的互相关性，避免了杂质对函数曲线的影响，保持了良好的单峰性，有效解决了在目标内容过于稀疏且受到表面杂质干扰时出现聚焦失败的问题。

5 结论

　　本文所提出的改进Vollath算法虽然存在波峰较宽的不足，但具有良好的无偏性和单峰性，特别是在含噪声、背景像素较多的情况下，比传统清晰度评价函数拥有更加优秀的抗噪性能。结合变步距渐进爬山算法，本文的自动搜索算法可以有效实现岩石薄片显微图像的自动聚焦。

参考文献

　　[1] 孙杰，袁跃辉，王传永.数字图像处理自动图像聚焦算法的分析和比较[J].光学学报，2007，27（1）：35-39.

　　[2] 申勤.数字图像清晰度评价函数的研究与改进[J].微型机与应用，2011，30（1）：32-33.

　　[3] 郭丙华，廖启亮，余志.基于小波变换的快速自动聚焦算法[J].中山大学学报（自然科学版），2007，46（2）：12-15.

　　[4] 郭军，曾文涵，谢铁邦.基于熵函数的快速自动聚焦方法[J].计量技术，2003（11）：30-32.

　　[5] 朱孔凤.自动聚焦区域选择算法[J].安徽大学学报（自然科学版），2009，33（2）：31-34.

　　[6] 莫春红，刘波，丁璐，等.一种梯度阈值自动调焦算法[J].红外与激光工程，2014（1）：323-327.

　　[7] HE J， ZHOU R Z， HONG Z L. Modified fast climbing search auto-focus algorithm with adaptive step size searching technique for digital camera[J]. IEEE Trans. on Consumer Electronics， 2003，49（2）：257-262.

　　[8] 张来线，孙华燕，郭惠超，等.基于图像灰度梯度最大值累加的自动调焦算法[J].光子学报，2013，42（5）：605-610.

　　[9] 翟永平，刘云辉，周东翔，等.稀疏图像内容情况下显微镜自动聚焦算法[J].软件学报，2012，34（5）：1281-1294.