摘  要： 提出一种基于最小外包矩形的快速椭圆拟合方法，该方法利用最小二乘法获得目标的最小外包矩形框，再求取外包矩形框的内切椭圆，该椭圆能有效反映目标的大部分运动信息。本文对该方法进行了目标拟合的有效性和实效性实验分析。分析表明，本算法得到的拟合椭圆内背景像素比例（Background Pixel Raito，BPR）相比于传统的矩形框和经典的Khachiyan椭圆拟合方法有了显著的下降，且拟合方法无需迭代运算，拟合速度仅次于传统的矩形框，比经典的Khachiyan椭圆拟合方法快3倍。本算法对于实时目标跟踪应用具有很好的应用价值。

　　关键词： 目标跟踪；椭圆拟合；最小二乘法；Khachiyan算法；矩形拟合框

0 引言

　　几何形状是一种常见的目标表示方法，如椭圆、矩形等[1-2]。在跟踪过程中，拟合的几何框面积越接近真实的运动目标，就越能真实地反应运动目标的各项参数。因此，目标的拟合率是目标检测与跟踪的一个重要指标[3]。特别是在多目标跟踪应用中，若运动目标的拟合几何框偏大，可能会导致两个运动目标的拟合框有一定程度的重合，两个拟合框之间相互影响，造成获取的目标特征不够准确。反之，若拟合几何框偏小，计算出的目标特征不够完整，也会影响跟踪效果[4]。

　　在目前的视频跟踪算法及应用中，矩形框是一种使用最多的目标表示方法，该方法利用目标四个方向最远边界点得到的矩形框来表示跟踪目标。这种矩形框虽然能够包含所有的目标信息点，但是往往包含较多的背景信息，因此可能造成遮挡、多目标重叠等问题[5]。针对此问题，国内外一些学者开始关注其他几何形状目标表示方法。其中，用最小面积的闭包椭圆来表示运动目标的方法受到了最多关注[6]。其原因是椭圆在很多目标表示方面（如人体、小汽车等）有着形状上的优势，不仅可以用更少的面积表示目标，而且椭圆的方向角度变化还能反映目标的一些行为动作[7]。

　　最小体积的闭合椭球模型（Minimum Volume Enclosing Ellipsoids，MVEE）是求解散点的最小闭包球的一种经典模型，许多学者提出了相关的求解方法，如Khachiyan算法[8]、KY算法[9]，Todd M.J.等人提出了相关的改进方法[10]，用于降低算法的复杂度和迭代次数。

　　Chaudhuri.D提出了一种闭合区域的最小边界框拟合方法，实现了对闭合区域的目标拟合最小的边界矩形框[11]。通过这种方法拟合出的矩形框可认为是目标的最小边界矩形框，不管从实际图像还是仿真图像的处理结果来看，该方法既精准又高效。

　　基于以上分析，本文根据最小二乘法求得目标的最佳外接矩形框，提出了一种基于外接矩形的椭圆拟合方法，该方法针对连续的前景目标拟合不需要迭代，速度快，效率高，拟合的椭圆面积与目标本身的面积接近，且椭圆中背景像素也相对较少。因此，该方法可以很好地近似表达视频中的运动目标，并解决多目标的重合问题，对噪声点有较好的鲁棒性。

1 最小外接矩形模型

　　最小外接矩形不同于常见的垂直矩形拟合框，最小外接矩形拟合过程如图1所示。具体步骤是：提取目标边界，计算目标中心，计算长短轴，寻找四个方向的最远边界点，计算出经过最远点的矩形框。

　　1.1 获取目标的边界

　　Sobel边缘检测器是一种常见的边缘提取工具，Sobel边缘检测器是利用特定的数字掩模图像进行滤波运算，Sobel边缘检测具有提取速度快的特点，本文利用Sobel算子提取目标的边界信息。

　　1.2 计算边界的中心

　　对于二维图像A，提取目标边界（xi，yi）（i=1，2…n）的中心坐标，通过以下公式计算得到：

　　1.3 利用最小二乘法计算长短轴

　　根据1.1，设经过目标中心的直线的倾斜角度为，则该直线的方程为：

　　目标边界点（xi，yi）（i=1，2…n）到该直线的距离为：

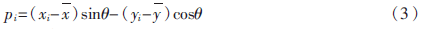
　　所有边界点到直线的距离平方和为：

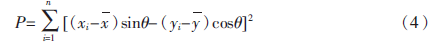
　　为了计算倾斜角度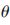，令距离平方和P最小情况下的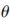即为所求，此时对方程（4）求偏导数，当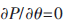时可以取得最优解，有：

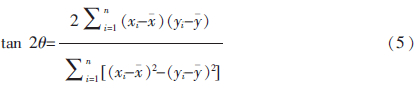
　　先计算出最优解下的直线倾斜角度，将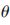代入式（2），所得的直线就是经过目标A中心的最佳拟合直线，且代表目标A的长轴倾斜方向，而目标的短轴，则是经过目标A的中心且垂直于长轴的直线。

　　1.4 分别找出上下左右四个方向距离长、短轴的最远点

　　由式（3）、（5），令函数f（x，y）=0，将目标A的边界点（xi，yi）（i=1，2…n）分别代入到长轴、短轴直线方程，有：

　　当f（a，b）>0时，该点位于长轴的上方；当f（a，b）<0时，该点位于长轴的下方；当f（a，b）=0时，该点刚好经过长轴直线。通过比较f（a，b）的值，可以区分开长短轴上面、下面的边界点，并找出f（a，b）的最大值和最小值，对应的点分别是pt（x1，y1），pb（x2，y2），pl（x3，y3），   pr（x4，y4）。

　　1.5 计算经过最远点且平行于矩阵轴线的直线方程

　　经过最上面的点的直线方程可以表示为：

　　（y-y1）-tan（x-x1）=0（6）

　　此直线即为目标的上边界外接矩形框直线，同理可以计算另外三条边的外界矩形框直线方程：

　　（y-y2）-tan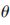（x-x2）=0（7）

　　（y-y3）+cot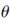（x-x3）=0（8）

　　（y-y4）+cot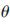（x-x4）=0（9）

　　1.6 计算直线交点，所得的矩形框即为最佳外接矩形

　　通过联立两条直线的方程，可以求出外接矩形框的顶点，联立式（6）、（8），可以求得矩形的左上交点坐标：

　　连接外接矩形四个顶点，即可得到目标的最佳外接矩形。

　　1.7 最小外接椭圆

　　求取最佳外接矩形时，可以求取目标的外接矩形的最大内切椭圆，该椭圆圆心即为外接矩形中心，长轴刚好等于外接矩形的长，短轴则等于外接矩形的宽，引入坐标旋转公式：

　　则矩形的内切椭圆即可通过参数方程表示为：

　　其中，a为椭圆的长轴，b为椭圆的短轴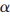，为椭圆长轴的倾斜角度。

2 实验结果及分析

　　本实验运行平台：Intel酷睿（i5 3470）四核处理器、8 GB内存的个人PC，计算仿真环境是MATLAB 2011a。在实验中，通过模拟多目标及实际视频序列两种输入分别比较了传统的矩形拟合框、质心法、VMEE模型中的Khachiyan算法与本文算法的拟合结果，选取椭圆大小及背景像素比例作为参考指标，分别计算了四种方法的执行效率。

　　图2（a）是一幅模拟二值图像，图像中包含了部分常见的几何形状，分别统计各个目标的像素个数，并计算拟合时间以及背景像素比例。

　　从图2中可以看出，（d）图中只有很少的点在椭圆外部，而椭圆内部的背景成分相比图（b）减少了很多。以目标3为例，通过计算可知，目标3的实际面积为  7 323个像素点，图2（b）中目标3椭圆的面积为9 583个像素点，背景像素的比例为0.26，拟合时间为2.25 s；图2（c）中椭圆的面积为10 261，背景的比例为0.32，拟合时间为0.33 s，图2（d）中椭圆面积为8 913，背景比例则降为0.19，拟合时间为0.07 s。

　　对视频序列进行目标拟合时，首先采用高斯混合模型对监控视频做前景检测，检测出运动目标后，对运动目标的拟合方法进行了对比分析：（1）传统矩形框拟合方法；（2）Khachiyan目标拟合方法；（3）基于质心的快速椭圆拟合方法；（4）本文算法。如图3所示。

　　图3是选取停车场监控画面的某一帧，对已经检测出的运动目标运用以上算法分别进行拟合运算。画面运动目标有两个，由于两个运动目标的距离较近，图3（a）中的矩形框几乎要重叠，且包含了大量的背景像素；图3（b）中的两个椭圆已经相交，多个运动目标的拟合框若相互交叠，在跟踪过程中，两个框内的特征会相互影响，导致跟踪时不能很好地区分当前像素属于哪一个目标；而图3（c）椭圆主轴方向与目标主轴方向不一致，而且两个拟合椭圆也已经相切，并没有有效地把两个目标区分开来；图3（d）中，目标信息全部包含在椭圆之内，而且拟合椭圆相互独立，能够更有效地还原真实目标运动情况。

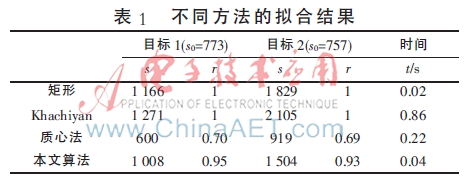
　　表1给出了图3中运动目标的面积、各个拟合框的面积、运算时间以及本文算法中椭圆内特征点的比例。由于运动目标是不规则的，因此把运动目标的像素点数作为它的面积。其中，s0为运动目标的面积；s为拟合框的面积；r为框内运动目标点的个数占总像素数的比例；t为程序运行时间。

　　从表1中可以看出，在停车场的监控画面中，无论从面积还是时间的角度考虑，传统矩形拟合方法都要优于Khachiyan算法，但是，这两种拟合框的面积也都远大于运动目标的面积。质心法虽然能获得最小的拟合椭圆，但是，其拟合率较低，损失了一部分重要信息。因此，本文提出的跟踪目标表示法在拟合框面积、运行时间以及框内目标点的比例三方面做到了较好的折中，拟合时间仅次于传统矩形拟合框，椭圆倾斜方向与目标方向一致，该方法还能解决多个运动目标因距离太近造成边界框交叠的问题。

3 结论

　　本文提出了一种基于最小外包矩形的快速椭圆拟合方法，该方法可以用于视频跟踪中运动目标的拟合。本算法利用最小二乘法求取运动目标的长、短轴及倾斜方向，并求取目标的最小外包矩形，截取矩形的内切椭圆即为目标的拟合椭圆。这种椭圆表示方法应用简单，不需要迭代，椭圆面积接近运动目标的实际面积，减少了拟合框中背景像素点的比例，能够避免多个运动目标在距离较近时发生的重叠问题。基于最小外包矩形的快速椭圆拟合方法能够快速拟合存在于二维图像里的运动目标，在以后的研究中，还可以探索在3D空间的目标拟合，以及存在于3D空间的散点集的拟合椭球模型。三维空间的目标拟合在三维重建领域具有十分积极的研究意义。

　　参考文献

　　[1] FIEGUTH P， TERZOPOULOS D. Color-based tracking of heads and other mobile objects at video frame rates[C]. In  IEEE Conference on Computer Vision and Pattern Recognition （CVPR）， 1997：21-27.

　　[2] COMANICIU D， RAMESH V， MEER P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2003，25（4）：564-575.

　　[3] YILMAZ A， JAVED O， SHAH M. Object tracking： a survey[J]. ACM Computing Surveys， 2006，38（4）：13-18.

　　[4] GLINEUR F. Pattern separation via ellipsoids and conic programming[M]. Belgium： Msthesis， Faculte Polythechnique de Mons， 1998.

　　[5] OLIVIER BARNICH， MARC VAN DROOGENBROECK. ViBe： a universal background substraction algorithm for video sequences[C]， IEEE Transaction on Image Processing， 2011：1709-1724.

　　[6] ZIVKOVIC Z， KROSE B. An EM-like algorithm for color-histogram-based object tracking[C]. IEEE Conference on Computer Vision and Pattern Recognition， 2004：798-803.

　　[7] JEPSON A， FLEET D，  ELMARAGHI T. Robust online appearance models for visual tracking[C]. IEEE Transaction on Pattern Analysis and Machine Intelligence， 2003， 25（10）： 1296-1311.

　　[8] KHACHIYAN L G. Rounding of polytopes in the real number model of computation[C]， Mathematics of Operations Research， 1996：307-320，

　　[9] KUMAR P， YILDIRIM， E A. Minimum volume enclosing ellipsoids and core sets[J]. Optimization Theory and Application， 2005，126（1）：1-21.

　　[10] TODD M J， YILDIRIM E A. On Khachiyan′s algorithm for the computation of minimum volume enclosing ellipsoids[J]. Discrete Application， 2007，155（13）：1731-1744.

　　[11] CHAUDHURI， D， SAMAL， A. A simple method for fitting of bounding rectangle to closed regions[C]. Pattern Recognit， 2007：1981-1989.