摘  要： 旅游客流量受多种因素影响，传统的时间序列预测模型无法描述预测对象的规律，人工智能方法如BP神经网络，其结构的选择过多依赖经验，基于此提出了利用改进的粒子群算法优化BP神经网络，通过惯性因子的非线性递减来改善粒子群的寻优性能。将该预测模型应用于自贡灯会的客流量进行实际预测分析，通过对150组训练样本和50组测试样本的实验仿真，可知改进后的方法提高了预测结果的准确度，并且涉及参数少、简单有效。

　　关键词： 旅游客流量预测；BP神经网络；粒子群算法；非线性递减

0 引言

　　随着中国旅游日的设立和国民旅游意识的增强，节假日旅游成了众多人的选择，但旅游目的地的接待能力有限，游客太多则旅游设施供不应求，服务质量下降，甚至出现游客拥堵、踩踏等安全事故。旅游景点游客量预测，一直是旅游研究中的热点，也是旅游学界面对的难点问题之一[1]。

　　传统的旅游需求预测，主要是定量与定性方面的研究，比如计量经济模型[2]、时间序列分析模型[3-4]、灰色预测模型[5]等方法。然而这些方法有一定的缺陷，或者是只分析单个影响因素，如客流量历史数据，认为未来是过去和现在的延续，或者是经验对预测方法的过度干扰，缺少对历史数据的学习过程。这些都会致使预测结果的不准确。另外，旅游景区每日客流量容易受到多个外部因素的影响，如天气、某些节假日等，具有较强的波动性和非线性，使用计量统计思想建立的模型难以逼近其内在变化机制。

　　由于具有良好的自适应性和强大的非线性映射能力，BP神经网络得到了广泛的应用，但其也存在着一些不足：一是网络模型训练前BP网络连接权值和阈值的随机初始化赋值，使得网络易陷入局部极值点，影响非线性学习能力，也即预测的精度；二是BP神经网络结构的确定，隐含层节点数没有确切的公式，选取不当易发生过拟合或学习能力不足[6-7]，影响网络的泛化能力。近年来人工智能算法优化BP神经网络的方法在不同领域也有一些应用，如宋国锋等[8]在改进遗传算法优化BP神经网络作预测的研究中，利用改进的遗传算法优化BP神经网络的结构和初始权重，而遗传算法有三个基本算子：选择、交叉和变异（算法的编程实现比较复杂），这三个算子的参数选择大部分依靠经验；程军等[9]在粒子群优化神经网络预测模型中，利用粒子群算法优化BP网络权重参数，该方法改善了BP网络易陷入局部极小值的不足，提高了收敛速度。粒子群算法具有遗传算法的大部分优点，并且训练操作简单，李雪等[10]通过粒子群算法的惯性权重和加速因子的线性递减，实现粒子的全局搜索与局部搜索之间的平衡，提高了寻优性能。

　　针对以上不足，结合以前学者的不同研究成果，提出非线性调整粒子群速度更新公式中的惯性因子的方法，根据样本数据源结构确定粒子群参数的初始化，用得到的粒子群的最优值初始化BP神经网络的权重，建立预测模型。

1 BP神经网络

　　BP神经网络是一种多层前馈神经网络，包括输入信号前向传递和误差反向传播两个过程。在结构上一般由输入层、隐含层、输出层三层构成，每一层的神经元状态只影响下一层神经元状态，它被广泛应用在各种预测模型中。在BP神经网络预测模型中，网络结构一般只需单个隐含层就能以任意精度逼近任意有理函数。训练样本的输入、输出向量的维数分别决定了网络的输入、输出层神经节点个数，典型的只有单个隐含层、单个输出的BP神经网络结构如图1所示。

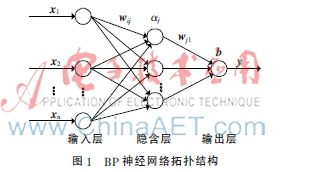
　　图1中，xi=（x1，x2，…，xn）为BP神经网络的一组输入向量，y为网络的目标输出值，wij为输入层与隐含层之间的连接权值，wj1为隐含层与输出层之间的连接权值，aj、b分别为隐含层和输出层的节点阈值。若设隐含层节点个数为m，则j=1，2，…，m，在前向传递中，输入信号向量xi从输入层经隐含层逐层传输，最后到输出层，通过各层连接权值矢量、阈值矢量和每一层相应的激励函数进行计算，得出输出层的预测输出值Y，若预测值Y与目标值y之间有误差，则误差部分转入反向逐层传递，沿误差减小方向调整网络各层连接的权值、阈值。反复执行以上过程，使得BP神经网络的预测值不断逼近实际输出值。

2 粒子群优化BP神经网络

　　2.1 基本PSO算法

　　粒子群算法（Particle Swarm Optimization，PSO）是于1995年由Kennedy和Eberhart首次提出的一种群体智能优化算法，该算法的实现方法简单，被广泛应用在许多优化问题中。

　　假设粒子群规模为M，该种群在给定的一个N维的搜索空间中组成一个种群T=（X1，X2，…，XM），粒子i在N维空间中的位置可表示为Xi=（xi1，xi2，…，xiN），速度表示为Vi=（vi1，vi2，…，viN），其中i=1，2，…，M。粒子i在寻找最优解的过程中第k次迭代时经过的最好位置记为Pik，群体在k时刻经过的最好位置记为Pgk，那么每次寻优迭代过程中，粒子i按式（1）来更新自己的速度和位置：

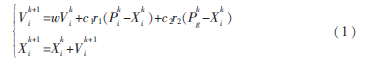
　　式中，k是迭代次数；c1为调节粒子向自身最优位置方向移动的步长，c2为调节粒子向全局最优位置方向移动的步长，它们是两个非负加速因子；r1和r2为位于[0，1]之间的常数。在粒子群算法中，为了控制Vik和Xik的各个分量在合理区域内，指定Vmax、Xmax，则Vi∈[-Vmax，Vmax]，Xi∈[-Xmax，Xmax]，一般会对速度向量进行最值限制，当Vi≥Vmax时，取Vi=Vmax；当Vi≤-Vmax时，取Vi=-Vmax。

　　2.2 改进PSO算法

　　基本粒子群算法有容易陷入局部最优和收敛精度差的不足，使得该算法的优化效果无法达到最佳。研究表明粒子的惯性因子w对算法的性能影响很大，w较大时有利于算法的全局搜索，而w较小时有利于算法的局部搜索。因此，选择一个合适的惯性权重很重要。有学者提出随着算法的迭代，w线性减小的方法，其表达式为：

　　w（k）=wmax-（wmax-wmin）（Tmax-k）/Tmax（2）

　　式中wmin为最小惯性权重，wmax为最大惯性权重，Tmax为粒子的最大迭代次数，k为当前迭代次数。其中，      0.1≤wmin≤wmax≤0.9，一般情况下，wmin=0.4、wmax=0.9时算法性能最好。

　　这种方法中w的变化与迭代次数是线性相关的，会使得算法不能很好地解决复杂的、非线性变化的优化问题。通过分析基本粒子群算法知，若线性调整粒子群的惯性因子，粒子局部搜索和全局搜索性能将有所下降。为解决线性递减方法调整的不足，这里采用非线性方法进行调整，此时的惯性因子表达式为：

　　w（k）=wmin+（wmax-wmin）exp（-25 k/Tmax）（3）

　　2.3 改进PSO-BP的算法实现

　　粒子群优化BP神经网络，首先要确定网络的拓扑结构，根据网络的拓扑结构确定粒子的长度，即粒子搜索空间的维数。其次，BP网络中权值和阈值的调整是以误差均方值为基准的，以粒子群优化的适应度函数作为BP网络误差的反传函数，建立误差均方值与粒子群算法适应度函数的对等关系，这样目标函数表达式：

　　式中，N表示训练样本总数，fi表示目标函数的误差平方和，y（k）、ym（k）分别表示目标函数的目标输出值和实际输出值。

　　改进粒子群算法的寻优，具体步骤如下：

　　（1）初始化粒子群参数：最大迭代次数Tmax、学习因子c1和c2、粒子群规模M、惯性权重wmax和wmin，在指定的位置与速度范围内随机初始化位置向量和速度向量。

　　（2）初始化BP神经网络，根据实际预测的问题确定BP神经网络的拓扑结构，建立网络模型，并根据网络的结构确定粒子的维度。

　　（3）输入网络的训练样本，将初始化的位置向量作为当前的全局最优值映射到网络的权值和阈值中，计算期望输出与实际输出的误差均方，并把它作为粒子群的适应度函数。

　　（4）根据粒子群速度、位置和惯性因子的改进公式，更新粒子的速度和位置。

　　（5）迭代运算，确定每个粒子的个体极值和全局极值：粒子i的适应度值fi与个体最优值pbest比较，如果小于pbest则取代它作为当前的个体最优；适应度值fi与全局极值gbest比较，如果小于gbest则取代它作为当前的全局最优。

　　（6）算法迭代停止时，将全局最优粒子位置映射到BP神经网络的权值和阈值中，作为BP网络权重值。

　　（7）将样本数据源中训练样本输入到已确定的网络模型中进行训练，用测试样本作预测。

3 改进的PSO-BP旅游客流量的预测

　　实验在MATLAB R2010b平台中编程实现。

　　3.1 数据集选定及预处理

　　实验数据为自贡灯会在每年的2~3月持续一个月左右的每日客流量及其他相关数据。通过灯会官方网站的电子商务订票系统、景点入口的电子红外扫描、窗口售票点、自贡气象局等方式，获取到的数据源参数有：昨日客流量x1、去年同期日客流量x2、窗口售票量x3、电子网站订票数量x4，天气信息w和周末假日h，通过这些参数预测目标值当日客流量y。

　　鉴于神经网络只能处理表示数值的输入数据，天气和周末假日是非数值量，并且其他影响因素不是同一量纲，在这里对不同天气状况和周末节假日等信息作如下变换：

　　（1）经分析在2~3月份灯会期间，自贡天气以阴天、多云天气为主，在此对天气信息作如下变换：

　　（2）分析发现，一周中周五、六、日三天观展人数较其余四天多，而周一至周四的游客人数基本接近，波动较小。周末假日信息作如下变换：

　　由于原始数据之间的数值相差较大，为了提高预测精确度，需要对原始数据进行归一化处理。归一化的方法很多，这里通过式（5）来处理：

　　其中，i=1，2，3，4；xmax表示数据集里的最大值，xmin表示数据集里的最小值。

　　3.2 实验仿真

　　以自贡灯会2009~2013年2~3月份的150组数据为训练数据集，以2014年2~3月份的30组数据为测试集，分别用来训练和测试网络模型，整个输入向量为6×180的矩阵。

　　改进PSO优化BP神经网络的初始参数确定：种群规模M=50，最大迭代次数G=200，输入节点数为6，输出节点数为1，隐含层节点个数取为15，共有6×15+15×1=105个权值，15+1=16个阈值，搜索空间维数N=105+16=121。建立6-15-1结构的BP网络。同时训练BP、PSO-BP预测模型，使用这三种模型对测试集进行预测，对比预测结果并作性能分析。

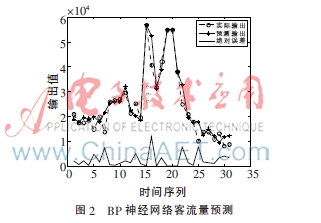
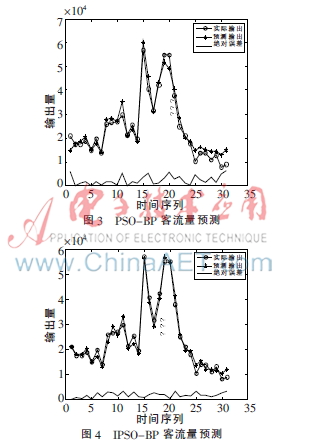
　　BP网络使用最小梯度下降法作为训练函数，目标误差精度为10-4；在标准PSO-BP中，加速因子选择c1=c2=2.0，其他参数选择与改进的PSO-BP网络的参数相同。图2、3、4分别为BP、PSO-BP、IPSO-BP当日预测客流量与实际人数的拟合图，并给出了两者的绝对误差曲线，其中横轴时间序列表示2~3月的时间量（每天），纵轴表示对应每天的景区客流量人数。

　　比较图2、3、4可知，利用惯性因子的非线性递减方法，预测曲线拟合度较高，预测的绝对误差明显减小。此时BP神经网络、PSO-BP神经网络和IPSO-BP神经网络的均方误差分别是：mseBP=1.4×10-3，msePSO-BP=4.76×10-4，mseIPSO-BP=3.42×10-4，可以看出改进后的预测精度有所提高。

4 结束语

　　本文提出改进的PSO-BP算法建立预测模型，并以自贡灯会客流量为例做预测分析。虽然选用的训练样本数据并不多，但从仿真结果看，却取得了较高精度的预测效果，说明粒子群算法无需过多原始数据也能得到理想的寻优结果。改进PSO和BP网络组合的预测模型简单有效，对自贡灯会的管理决策有较大的参考价值。如何进一步提高算法在法定节假日、异常天气情况下的客流量预测的泛化能力，是下一步研究的重点。

　　参考文献

　　[1] 陶伟，倪明．中西方旅游需求预测对比研究：理论基础与模型[J]．旅游学刊，2010，25（8）：12-17．

　　[2] SMERAL E， WITT S F， WITT C A． Econometric forecasts： tourism trends to 2000[J]． Annals of Tourism Research，1992，19（3）：450-466．

　　[3] 陈萍萍．基于时间序列的旅游需求预测模型[J]．统计与决策，2013（18）：11-13．

　　[4] 赵娟，江立辉．旅游客流量预测的模糊时间序列模型以黄山风景区为例[J]．合肥学院学报（自然科学版），2014，24（4）：26-31．

　　[5] ZENG Z L， ZHENG Y． The grey model and its application to forecast of inbound visitors from mainland China to Macau[C]． 3rd Intrmational Conference on Management Science and Engineering Management， 2009：48-54．

　　[6] 李松，刘力军，翟曼．改进粒子群算法优化BP神经网络的短时交通流预测[J]．系统工程理论与实践，2012，32（9）：2045-2049．

　　[7] 王德明，王莉，张广明．基于遗传BP神经网络的短期风速预测模型[J]．浙江大学学报（工学版），2012，46（5）：837-841．

　　[8] 宋国锋，梁昌勇，梁焱，等．改进遗传算法优化BP神经网络的旅游景区日客流量预测[J]．小型微型计算机系统，2014，35（9）：2136-2141．

　　[9] 程军，李荣钧．基于粒子群优化的神经网络预测模型[J]．教学的实践与认识，2015，45（3）：176-180．

　　[10] 李雪，顾沈明，年浩．改进粒子群算法优化BP神经网络的粮食产量预测[J]．漳州师范学院学报（自然科学版），2014，27（1）：56-61．