摘  要： 利用服务基站与移动台之间的场强测量值来进行移动台位置估计，并从场强信号传播模型和定位算法出发，提出了一种基于小波变换的改进场强定位算法。通过小波变换来修正传播误差，然后利用LS算法进行定位。仿真结果表明，该基于场强的移动台定位方法在一定程度上提高了定位精度，定位效果明显优于Chan算法、LS算法、Taylor算法。

　　关键词： 传播模型；小波变换；场强定位；LS算法

0 引言

　　在移动通信传播环境中，电波在传播路径上遇到起伏的山丘、建筑物、树林等障碍物阻挡，形成电波的阴影区，就会造成信号场强中值的缓慢变化，引起衰落，从而大大降低了定位精度。目前来看，常用的定位方法有到达时间[1]（TOA）定位、到达时间差[2]（TDOA）定位、到达角度[3]（AOA）定位、场强[4]（SOA）定位、场强差[5]（SDOA）定位以及融合定位[6]等。综合各种定位方法来看，场强定位方法通过改进算法就可以得到较好的定位效果，对物理设备以及移动终端要求较低，大大降低了成本，容易实现。但由于场强信号在传播过程中容易受到外界因素影响，使得测量值与真实值之间存在较大误差，从而对定位精度产生影响。

　　小波变换[7-8]是一种新兴的数学分支，它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶；在应用领域，特别是在信号处理、图像处理、语音处理以及众多非线性科学领域，它被认为是继Fourier分析之后的又一有效的时频分析方法。小波变换在信号消噪处理中有比较明显的效果，由于噪声一般处在信号的高频部分，而有用信号一般处在信号频谱的低频部分，因而能有效地从信号中提取信息。本文用小波变换对传播误差进行修正，再进行定位，最后利用MATLAB进行仿真，并对仿真得到的结果进行分析和比较。

1信道模型

　　实际生活中信号的传播环境千差万别，不同地形、地貌、建筑物等参数都会影响无线网络的规划，传播模型可以表征在某种特定环境或传播路径下点播的传播损耗情况。随着移动通信网络的飞速发展，各大运营商也越来越重视传播模型与本地区环境相匹配的问题。因此要通过场强进行信号定位，就必须根据不同传播环境选择不同的传播模型，从而进一步改善定位效果。如今，已经有适应不同地形环境的场强衰落模型，例如Okumura Hata[9]、COST-231[10]、Okumura、Egli、WIM、Walfish模型等。其中Okumura Hata模型是根据实测数据建立的模型，适用于平坦地面宏蜂窝点播传播模型，能提供比较全面的数据，因此在实际移动台定位中得到了广泛应用。其适用频率为150 MHz~1 500 MHz，基站天线高度范围为30~200 m，移动台天线高度范围为1~10 m，传播距离范围为1 km~20 km。不同传输环境下的损耗预测公式为：

　　Lc=69.55+26.16log10（fc）-13.82log10（hb）-a（hm）+

　　[44.9-6.55log10（hb）]log10（d）（1）

　　其中，hm为MS天线高度（m）；fc为载波中心频率（MHz）；hb为BS天线高度（m）；d为MS与BS之间的距离（km）；a（hm）是移动台天线高度的有效修正因子，传播环境不同其取值也不同，分别如下：

　　中小城市修正：

　　a（hm）=（1.1log10（fc）-0.7）hm-（1.56log10（fc）-0.8）（2）

　　大城市修正：

　　a（hm）=8.29[log10（1.54hm）]2-1.1（f≤300 MHz）（3）

　　a（hm）=3.2[log10（11.75hm）]2-4.97（f≥300 MHz）（4）

　　郊区：

　　Ls=Lc-2[log10（f/28）]2-5.4（5）

　　半开阔地：

　　Lv=Lc-4.78[log10（fc）]2-18.33log10（fc）-40.98（6）

　　通过上述模型校正有利于对一个新的服务覆盖地区的信号进行仿真预测，可以大大降低实际路测所需的时间、人力和资金，可以提高网络的服务质量。基于上述传播模型可以求出信号的路损值，由于信号的路损值与场强之间存在着一定的线性关系，用E来表示场强值，则根据上述模型得出的场强模型为：

　　市区：Ec=Pbs-Lc-Gr（7）

　　郊区：Es=Pbs-Lc-Gr（8）

　　宽阔地区：Ev=Pbs-Lv-Gr（9）

　　其中，Pbs为BS的发射功率（dB），Gr为接收天线增益（dBi）。经过大量的实验表明，当Gr=24 dB时，移动终端的场强实际测量值与本文的场强模型预测值最接近。以郊区小区为例，把式（5）带入式（8）即可得到：

　　E（di）=alog10（di）+b（10）

　　2 算法描述

　　2.1 小波变换

　　小波变换克服了短时傅里叶变换在单分辨率上的缺陷，具有多分辨率分析的特点，在时域和频域都有表征信号局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整，在一般情况下，在低频部分（信号较平稳）可以采用较低的时间分辨率而提高频率的分辨率，在高频情况下（频率变化不大）可以用较低的频率分辨率来换取精确的时间定位。因为这些特点，小波分析可以探测正常信号中的瞬态，并展示其频率成分，被称为数学显微镜，广泛应用于各个时频分析领域。小波变换形象地说就是一个滤波器组，可以提取不同频率的信息，因此通过这种方法就可以在有些频带系数上集中信号能量，于是可以通过小波系数置零或是赋予小的权重来过滤掉不需要频带上的信息，从而有效地抑制噪声。

　　设x（ti）为在ti时刻的场强测量值，则有：

　　x（ti）=s（ti）+u（ti）+NLOS（ti）（11）

　　其中，s（ti）是ti时刻的真实测量值，u（ti）是ti时刻的传播误差，NLOS（ti）是均值为零且服从高斯分布的随机序列。对时变s（t）∈L2（R）进行正交小波分解[11]，得到：

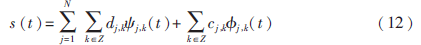
　　通过小波变换消除噪声步骤如下：

　　（1）通过各基站可以得到输入向量为：S=[SOA1，SOA2，SOA3，SOA4，SOA5，SOA6，SOA7]。选择合适的小波函数，然后通过小波变换对测量得到的场强信号选择合适的小波分解层数进行分解，从而得到对应的小波变换系数。

　　（2）可以由如下经验公式来计算均方误差在不同尺度下的值。

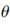　　j=median（|dj，k|）/0.674 5（13）

　　（3）由步骤（2）中得到的均方误差，使用如下固定阈值算法计算出不同尺度系数的阈值，然后对步骤（1）中的下拨系数进行取舍，从而得到新的小波系数。

　　（4）对步骤（3）中得到的新的小波系数进行小波逆变换，得到重构去除噪声后的数据测量值。

　　2.2 定位算法

　　2.2.1 基于场强的LS定位算法

　　根据MS和BS之间的距离，采用LS算法来估计移动台的位置。设MS坐标为（x，y），BS坐标为（xi，yi），便可得到下面的方程式：

　　并且由式（10）可得到：

　　由式（15）和式（16）相等且ki=xi2+yi2，xi，1=xi-x1，yi，1=yi-y1，（其中d1为MS与服务基站之间的距离，可由TA值计算出来），可以得出：

　　Ai+ki+k1=-2xxi，1-2yyi，1（17）

　　通过式（16），令h=GaZa，当SOA包含测量误差时，可得到如下方程：

　　由以上各公式可得到MS位置为：

　　Za=（GaTGa）-1GaTh（19）

　　2.2.2 基于小波分析的LS定位算法

　　场强信号在传播过程中很容易受外界因素的影响，通过小波变换对场强测量数据进行修正，进而减小传播误差对测量值的影响，最后通过LS定位算法进行移动台定位，从而有效提高定位精度。定位的具体步骤如下：

　　（1）先测得K组带有传播误差的SOA信号数据，然后通过小波变换对其进行正交小波分解得到对应的系数；

　　（2）对步骤（1）中得到的系数进行逆变换，重构出去除噪声的场强信号；

　　（3）利用步骤（2）中的场强数据通过LS算法来进行移动台位置估计。

3 仿真及分析

　　对提出的基于小波变换的场强定位方法用MATLAB进行仿真，仿真结果及分析如下。

　　图1为不同小区半径下本文的场强定位算法与Chan算法、LS算法、Taylor算法仿真结果对比图，纵坐标为各种算法的均方误差，横坐标为小区半径。当小区半径增加时，传播误差也会随着传播距离的增大而增加，由图可以看出，各种定位算法的均方误差也会相应地有所增加，但相比之下本文算法由于利用小波变换进行了消噪处理，使得信号传播受距离的影响较小，性能比较稳定，说明小波变换可以很好地消除传播误差。

　　图2为不同测量误差下基于小波变换的场强定位算法与Chan算法、LS算法、Taylor算法仿真结果对比图，纵坐标为均方误差，横坐标为不同的测量误差。当测量误差逐渐增大时，传播误差也会逐渐增大，从而导致各种定位算法、定位精度都存在某种程度的下降，但通过小波优化后的场强定位由于很大程度上消除了传播误差的影响，故当测量误差增大时所受影响较小，定位效果优于Chan算法、LS算法、Taylor算法。

4 结论

　　本文提出了一种基于小波变换的场强定位算法，在不同的传播环境下有不同的修正因子从而确定不同的传播算法。通过小波变换配合相应的阈值对测量数据进行处理得到新的小波系数，从而有效地减小了传播误差以及系统测量误差对定位精度的影响，最后利用LS算法进行移动台位置估计。从实验的模拟仿真可以看出，本文提出的算法与Chan算法、LS算法、Taylor算法相比，定位精度更高，性能更稳定，有良好的可行性。

参考文献

　　[1] 徐彤阳.NLOS环境下无线传感器网络TOA定位算法[J].计算机工程，2013，39（12）：93-96.

　　[2] 熊瑾煜，王巍，朱中梁.基于秦勒级数展开的蜂窝TDOA定位算法[J].通信学报，2004，25（4）：144-150.

　　[3] 田孝华，廖桂生.减轻TOA和AOA定位系统非视距影响的方法[J].电子与信息学报，2003，25（12）：1664-1667.

　　[4] 王建军，邓平，李金伦.一种基于场强差的GSM网络移动台定位方法[J].专题技术与工程应用，2006，36（8）：52-64.

　　[5] BENSLEY S， AAZHANG B. Subspace-based channel estimation for code division multiple access communication systems[J]. IEEE Transaction on Communications， 1996，44：1009-1020.

　　[6] 范平志，邓平，刘林.移动台定位估计数据融合增强模型及其仿真研究[J].通信学报，2003，24（11）：166-171.

　　[7] 张阳，王嘉梅.一种改进的小波变换域的字符定位方法[J].微型机与应用，2011，30（18）：35-37.

　　[8] 张仁辉，杜民.小波分析在去噪中的应用[J].计算机仿真，2005，22（8）：69-72.

　　[9] RAPPAPORT T S.无线通信原理与应用[M].蔡涛，李旭，杜振民，译.北京：电子工业出版社，1999.

　　[10] 付昆鹏.无线通信中电波传播模型的研究[D].广州：华南师范大学，2009.

　　[11] 卓宁.小波分析技术在GPS数据预处理中的应用[J].中国惯性技术学报，2009，17（2）：184-186.