摘  要： 针对梯形箱子的三维装箱问题，提出了一种基于空间分割的构造性启发式算法，根据梯形箱子三维装箱问题的特点，设计了相应的空间分割策略、空间合并策略与空间重组策略，在此基础上加入遗传算法，提高算法局部与全局搜索能力。实验结果表明，该算法能有效处理梯形箱子三维装箱问题。

　　关键词： 三维装箱问题；启发式算法；遗传算法

0 引言

　　装箱问题（Bin Packing Problem）在现实生活中具有广泛的应用。计算机领域中有内存分配、信息存储等一维装箱问题；二维装箱问题应用于服装裁剪、新闻排版、矩形装箱[1]等；在货运码头、物流、仓储等领域则涉及三维装箱问题。

　　装箱问题是NP难问题，需要考虑维数、形状、约束、目标等不同因素，因此理论研究与实际工程应用中一般采用近似算法。近年来，国内外学者对三维装箱问题进行了广泛而深入的研究。三维装箱问题存在禁忌搜索算法[2]、遗传算法[3-4]、模拟退火算法[5]等研究和应用。参考文献[6]采用动态空间分解方法进行启发式装载，其对剩余空间进行重组优化存在不足；参考文献[5]提出了混合模拟退火算法，从一个初始货物装载序列采用模拟退火搜索一个好的货物装载序列，作为问题的近似解；参考文献[7]通过组织装填树把大空间分成小空间进行装填，最后再对剩余空间进行处理，其通过搜索局部最优解进行装填，全局搜索能力需要提高；另外还有一些基于“块”的启发式算法[8-10]与运用“墙”的建立与穴度方法相组合的启发式算法[11]，这些启发式算法是面向长方体箱子三维装箱问题算法研究应用，而没有涉及到梯形箱子的三维装箱问题。

　　在实际工程应用中存在非长方体箱子三维装箱问题，例如，箱子几何形状为上下底面为直角梯形的直四棱柱等特殊类型的箱子。这需要根据具体装箱问题的特点与实际工程应用要求，研究相应的装箱算法来完成货物装箱。

　　本文研究的梯形箱子三维装箱问题的具体描述为：给定无限数量相同规格的梯形箱子，给定有限数量的待装长方体货物，在满足装载约束的条件下把这些长方体货物全部装入梯形箱子中，目标是梯形箱子使用数目最少，使空间利用率最高。

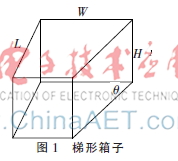
　　定义1（梯形箱子） 梯形箱子的几何形状是上下底面为直角梯形的直四棱柱，在图1中，其几何形状可以通过底面直角梯形的高度L、底面直角梯形的下底边W、底面直角梯形的锐角θ以及直四棱柱高度H来描述。

　　装载约束条件如下：

　　（1）每个装载的货物不能与其他装载货物或者梯形箱子互相重叠；

　　（2）每个装入梯形箱子的货物的每一个面必须与梯形箱子的某一个面平行；

　　（3）每个装入梯形箱子的货物必须满足方向约束。

1 基于空间分割的构造性启发式算法

　　针对梯形箱子三维装箱问题，本文提出了一种基于空间分割的构造性启发式算法。该算法思想借鉴了Bortfeld和Gehring[2]中提到的基础启发式算法。

　　1.1 空间分割

　　在装箱问题中，所有装入的货物都是与坐标轴平行的长方体，对它们的装载位置描述是通过参考点与各个维度上的边长来确定的。图2中空间直角坐标系的X轴、Y轴、Z轴分别与梯形箱子长度L、宽度W、高度H方向平行，梯形箱子左后下角为原点O。

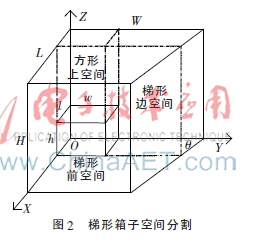
　　定义2（方形空间）方形空间i由其几何形状长度Li、宽度Wi和高度Hi，以及空间坐标参考点（xi，yi，zi）构成，数学表达方式：

　　cspacei={（Li，Wi，Hi），（xi，yi，zi）}（1）

　　定义3（梯形空间）梯形空间i由其几何形状长度Li、宽度Wi、高度Hi和底面直角梯形的锐角θ，以及空间坐标参考点（xi，yi，zi）构成，数学表达方式：

　　tspacei={（Li，Wi，Hi，θi），（xi，yi，zi）}（2）

　　把梯形箱子作为一个梯形空间tspacei，当某个长宽高为（lj，wj，hj）的货物j满足梯形空间约束时，该货物装入梯形空间的空间坐标参考点（xi，yi，zi）即原点O，剩余空间被分割成3个子空间：

　　方形上空间

　　cspacea={（lj，wj，Hi-hj），（xi，yi，zi+hj）}（3）

　　梯形边空间

　　tspaceb={（lj，Wi-wj，Hi，θi），（xi，yi+wj，zi）}（4）

　　梯形前空间

　　tspacec={（Li-lj，Wi-lj/tanθi，Hi，θi），（xi+lj，yi，zi）}（5）

　　梯形空间约束：

　　当货物j装入梯形空间tspacei时需满足：

　　lj≤Li且hj≤Hi且（wj+lj/tanθi）≤Wi（6）

　　由所有子空间构成一个空间集合S，从空间集合中选择一个子空间，若是梯形空间则分割方法如上，若是方形子空间则采用方法如下：

　　选择一个方形空间cspacei，当某个长、宽、高为（lj，wj，hj）的货物j满足方形空间约束时，该货物装入方形空间的空间坐标参考点（xi，yi，zi），剩余空间被分割成3个子空间：

　　方形上空间

　　cspaced={（lj，wj，Hi-hj），（xi，yi，zi+hj）}（7）

　　方形边空间

　　cspacee={（lj，Wi-wj，Hi），（xi，yi+wj，zi）}（8）

　　方形前空间

　　cspacef={（Li-lj，Wi，Hi），（xi+lj，yi，zi）}（9）

　　方形空间约束：

　　当货物j装入方形空间cspacei时需满足：

　　lj≤Li且hj≤Hi且wj≤Wi（10）

　　1.2 启发式算法

　　基于空间分割的启发式算法基本步骤表述如下：

　　（1）算法开始，初始化待装货物序列C与梯形箱子信息。

　　（2）判断待装货物是否装载完成，装载完成跳转（7）；反之，未完成装载则跳转到（3）。

　　（3）选择一个待装货物并开启一个新的梯形箱子，待装货物装入梯形箱子后剩余空间被分割成3个子空间，分别为方形上空间、梯形边空间与梯形前空间，这3个子空间组成新的空间序列S，把装入的货物从待装货物序列C中移除，完成待装货物序列C更新。

　　（4）判断待装货物序列C中是否存在一个货物满足装载约束并能装入空间序列S中某个空间，存在该货物则跳转（5）；反之，则跳转到（6）。

　　（5）若该空间为梯形子空间，装入选择的货物后，剩余空间被分割为方形上空间、梯形边空间与梯形前空间这3个子空间；若该空间为方形子空间，则装入选择的货物后，剩余空间被分割为方形上空间、方形边空间与方形前空间这3个子空间；该空间装入货物后从空间序列S中移除，新生成的3个子空间添加到空间序列S中，同时通过空间合并策略更新空间序列S，装入的货物从待装货物序列C中移除，完成待装货物序列C更新。

　　（6）判断是否进行过重组策略操作，没有则对空间序列S进行重组策略操作，跳转（4）；若进行过重组策略操作则跳转到（2）。

　　（7）输出梯形箱子三维装箱方案，算法结束。

　　定义4（空间合并策略）若2个方形子空间cspace1={（L1，W1，H1），（x1，y1，z1）}、cspace2={（L2，W2，H2），（x2，y2，z2）}能够满足以下条件中的一个：

　　条件1：（L1+x1==x2||L2+x2==x1）&&（y1==y2）&&（W1==W2）&&（z1==z2）&&（H1==H2）（11）

　　条件2：（W1+y1==y2||W2+y2==y1）&&（x1==x2）&&（L1==L2）&&（z1==z2）&&（H1==H2）（12）

　　则2个方形子空间合并为新的方形子空间cspace3。

　　若满足条件1，则：

　　if x1<x2 cspace3={（L1+L2，W1，H1），（x1，y1，z1）}；（13）

　　if x2<x1 cspace3={（L1+L2，W2，H2），（x2，y2，z2）}；（14）

　　若满足条件2，则：

　　if y1<y2 cspace3={（L1，W1+W2，H1），（x1，y1，z1）}；（15）

　　if y2<y1 cspace3={（L2，W1+W2，H2），（x2，y2，z2）}；（16）

　　空间合并策略是把2个能合并的子空间合并成一个更大的子空间，提高箱子的空间利用率。

　　图3（a）为满足条件1的空间合并示意图，图3（b）为满足条件2的空间合并示意图。

　　定义5（空间重组策略）若2个方形子空间cspace4={（L4，W4，H4），（x4，y4，z4）}、cspace5={（L5，W5，H5），（x5，y5，z5）}能够满足以下条件中的一个：

　　条件3：（L4+x4==x5||L5+x5==x4）&&（y4==y5）&&（W4==W5）&&（z4+H4==z5+H5）（17）

　　条件4：（W4+y4==y5||W5+y5==y4）&&（x4==x5）&&（L4==L5）&&（z4+H4==z5+H5）（18）

　　则2个方形子空间重组为新的方形子空间cspace6。

　　令H6=min（H4，H5），z6=max（z4，z5）；（19）

　　若满足条件3，则：

　　if x4<x5 cspace6={（L4+L5，W4，H6），（x4，y4，z6）}；（20）

　　if x5<x4 cspace6={（L4+L5，W5，H6），（x5，y5，z6）}；（21）

　　若满足条件4，则：

　　if y4<y5 cspace6={（L4，W4+W5，H6），（x4，y4，z6）}；（22）

　　if y5<y4 cspace6={（L5，W4+W5，H6），（x5，y5，z6）}；（23）

　　空间重组策略是充分利用剩余的子空间，有利于提高箱子的空间利用率。图4为空间重组示意图。

2 面向梯形箱子三维装箱的混合遗传算法

　　针对梯形箱子三维装箱问题这一NP难问题，结合启发式算法局部搜索能力与遗传算法全局搜索能力，混合遗传算法不仅局部搜索能力得到加强，而且兼具全局搜索能力。

　　2.1 编码方案

　　根据梯形箱子三维装箱问题的具体情况，采用顺序编码，每个个体由待装货物编号序列PN以及其对应的摆放方向序列PD组成。货物的摆放方向有6种，对应编号1为（l，w，h）、编号2为（w，l，h）、编号3为（w，h，l）、编号4为（h，w，l）、编号5为（l，h，w）、编号6为（h，l，w）。

　　2.2 适应度函数

　　通过个体适应度的大小来评价群体中个体所对应装载方案的优劣。这里选择整体梯形箱子三维装箱空间利用率作为适应度函数：

　　其中，M表示装载了M个货物，lj，wj，hj表示第j件货物的长度、宽度和高度；N表示使用了N个梯形箱子，Vi表示第i个梯形箱子的体积。

　　2.3 遗传操作

　　采用轮盘赌选择方法作为选择算子，在轮盘赌选择中，各个个体的选择概率与其适应度值成正比例。

　　采用部分匹配交叉（Partally Matched Crossover，PMX）算子，在PMX操作中，先依据均匀随机分布产生两个位串交叉点，这两点之间的区域为一匹配区域，并使用位置交换操作交换两个父串的匹配区域。

　　对进行变异操作的个体，随机产生2个位置i、j，交换处在位置i与位置j上的货物编号信息n及对应的货物方向信息；存在一定变异概率使得货物摆放方向变异。变异算子的作用是维持群体的多样性，避免算法早熟收敛。

　　图5为面向梯形箱子三维装箱的混合遗传算法流程图。

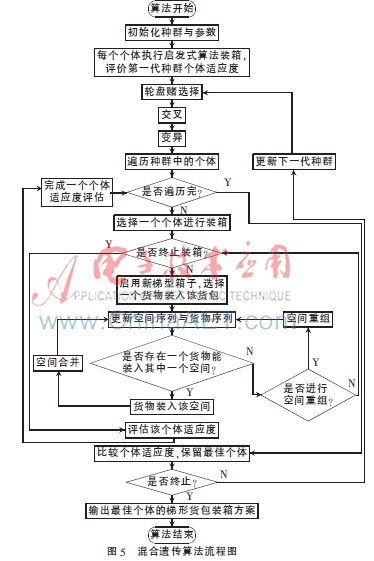
3 实验结果

　　表1中测试用例1~4，使用梯形箱子参数为L=400、W=800、H=400、tanθ=1；测试用例5~8，使用梯形箱子参数为L=400、W=600、H=400、tanθ=2；测试用例9~12，使用梯形箱子参数为L=400、W=900、H=400、tanθ=0.8；混合遗传算法参数设置：种群大小20、进化代数100、交叉概率0.5、变异概率0.05；每个测试用例进行100次实验。本文混合遗传算法与混合模拟退火算法[5]进行比较。

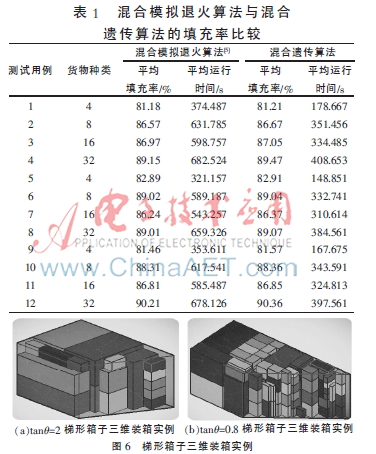
　　表1的实验结果显示，在面向梯形箱子三维装箱问题上，通过与混合模拟退火算法比较，混合遗传算法的解不仅平均空间填充率较高，而且平均运行时间较短。混合遗传算法能有效处理梯形箱子三维装箱问题。

　　图6中，（a）是测试用例5的一个空间填充率为87.24%的梯形箱子三维装箱布局方案实例，（b）是测试用例12的一个空间填充率为92.11%的梯形箱子三维装箱布局方案实例。

4 结论

　　借鉴Bortfeld和Gehring[2]的长方体空间基础启发式算法思想，根据梯形箱子的空间约束条件，研究设计了面向梯形空间的构造性启发式算法。采用空间分割策略、空间合并策略与空间重组策略提高局部搜索能力。其与遗传算法全局搜索能力相结合，设计了面向梯形箱子三维装箱问题的混合遗传算法。理论分析与实验结果显示，针对梯形箱子三维装箱问题，混合遗传算法具有良好的优化效果。希望本文的研究对三角形箱子、楔形箱子等特定类型箱子三维装箱问题的研究提供一些帮助和借鉴。

　　参考文献

　　[1] 陈胜达，张德富，刘艳娟.求解矩形装箱问题的一种近似算法[J].计算机工程，2007，33（9）：189-193.

　　[2] BORTFELDT A， GEHRING H， MACK D. A parallel tabu search algorithm for solving the container loading problem[J]. Parallel Computing，2003，29（5）：641-662.

　　[3] BORTFELDT A， GEHRING H. A hybrid genetic algorithm for the container loading problem[J]. European Journal of Operational Research，2001，131（1）：143-161.

　　[4] GEHRING H， BORTFELDT A. A parallel genetic algorithm for solving the container loading problem[J]. International Transactions in Operational Research，2002，9（4）：497-511.

　　[5] 张德富，彭煜，朱文兴，等.求解三维装箱问题的混合模拟退火算法[J].计算机学报，2009，32（11）：2148-2156.

　　[6] WANG Z， LI K W， LEVY J K. A heuristic for the container loading problem： a tertiary-tree-based dynamic space decomposition approach[J]. European Journal of Operational Research，2008，191（1）：86-99.

　　[7] LIM A， RODRIGUES B， YANG Y. 3-D container packing heuristics[J]． Applied Intelligence，2005，22（2）：125-134.

　　[8] 张德富，彭煜，张丽丽.求解三维装箱问题的多层启发式搜索算法[J].计算机学报，2012，35（12）：2554-2561.

　　[9] MIYAZAWA F K，.WAKABAYASHI Y. Three-dimensional packings with rotations[J]. Computers & Operations Research，2009，36（10）：2801-2815.

　　[10] ELEY M. Solving container loading problems by block arrangement[J]. European Journal of Operational Research，2002，141（2）：393-409.

　　[11] Wu Xiuli， Du Yanhua， Li Sujian. A new approach for the three-dimensional single container loading problem[C]. Intelligent Human-Machine Systems and Cybernetics （IHMSC）， 2013 5th International Conference on， 2013：155-158.

　　[12] 陈国良，王煦法，庄镇泉，等.遗传算法及其应用[M].北京：人民邮电出版社，1996.