摘 要: 基于模糊粗糙集模型构建模糊等价关系是混合数据分析的有效方法之一。针对属性类别多样性的混合型信息系统,提出一种带权的对象间相似性度量方法,该方法建立每类属性对应的相似性度量函数,再通过归并确立带权的模糊相似矩阵。在转化为模糊等价关系的基础上,采用加入蕴含专家领域知识及用户需求的约简算法。通过数据库中几个数据集样本对属性约简后的数目、精度进行对比,验证了方法的有效性和可行性。
关键词: 模糊粗糙集模型;模糊等价关系;混合数据;模糊相似矩阵;约简
0 引言
粗糙集理论是一种以精确的数学形式处理不确定信息的数学工具,属性约简在保持分类能力不变的前提下获得最小特征子集,是粗糙集理论的核心应用之一。经典粗糙集理论[1-3]通常是处理只包含符号型属性的数据模型,而实际的信息系统中属性和决策的值域是多样性的,有符号型属性,也有连续数值型属性,即混合分类数据。对于混合数据的处理大体可分为两类:一类是离散化方法[4],将数值型属性转化为符号型属性的数据形式,即在数值属性值域中选择合适的分割点,划分成若干由字符标记的不同区域,从而将不同类别属性转化为统一的数据形式再进行约简。如何选择分割点引出了离散化方法的系统分析比较[5],讨论的关键在于分割点数量和位置的设计,缺点在于产生了量化误差,丢失了同种符号表示的区域内不同属性值间的序信息。另一类是对不可分辨关系进行拓展的混合型方法。Hall提出了利用信息熵计算符号变量相关性的特征选择方法[6],Zhou和Qian提出了采用定性信息分解复杂问题的决策树构造方法[7],以及之后提出的混合数据特征选择的方法[8],缺点都是将符号型属性和数值型属性割裂开分析,丢失了分类能力较强的数值属性信息。Kwak和Choi、Peng等人陆续采用Parzen窗方法计算数值型样本概率密度来进行特征选择[9],取得了一定进展。Zadeh提出了模糊集理论[10],认为模糊信息粒化在知识发现过程中极其重要,模糊粗糙集和粗糙模糊集概念的提出,融合了模糊粒化和粗糙逼近两种不确定方法[11-15],使得约简结果能更清晰地体现信息系统的分类能力。Hu采用信息熵的概念度量信息系统的分类能力,在混合数据的处理过程中,得到的对象间相似矩阵数值单一,且整合符号型和数值型属性的过程中丢失很多分类信息[16]。遗传算法应用于混合数据约简的方法,由于本身算法的特点导致计算量大、耗时长[17-18]。
本文重点研究在模糊粗糙集模型框架下如何定义混合数据间带权的相似性度量方法及模糊等价关系,通过定义不同类别属性对应的相似性度量函数,以及带权的模糊相似矩阵,最终确定模糊等价关系;之后通过加入领域专家的经验知识和系统客户的需求偏好对数据进行约简,将约简后的属性数目、精度与其他方法的数据进行对比,以验证方法的有效性和可行性。
1 模糊等价关系及其度量
针对符号型变量的处理,可以利用粗糙集在等价关系的基础上建立对象间关系。但对于数值型变量,等价关系不足以清晰地刻画对象间关系,需要借助模糊等价关系的概念。
给定信息系统S=(U,A),论域U={x1,x2,…,xn},属性集合A=C∪D是条件属性和决策属性的集合,且C∩D=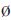 。本文讨论的混合信息系统的属性集合既有条件属性,也有数值属性。
。本文讨论的混合信息系统的属性集合既有条件属性,也有数值属性。
定义1:给定一个矩阵A=(aij)n×n,若对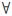 i,j=1,2,…,n,满足:(1)自反性:aii=1;(2)对称性:aij=aji;(3)模糊性:aij∈[0,1];(4)传递性:aij≥∨k(aik∧akj),则称矩阵A为模糊等价矩阵。
i,j=1,2,…,n,满足:(1)自反性:aii=1;(2)对称性:aij=aji;(3)模糊性:aij∈[0,1];(4)传递性:aij≥∨k(aik∧akj),则称矩阵A为模糊等价矩阵。
在以下论述中,用M(R)=(rij)n×n来表示二元关系R的关系矩阵,其中R满足模糊等价关系。

定义4[16]:给定模糊信息系统<U,A,V,f>,A=C∪d,若H(d|B-a)=H(d|B),则属性a是冗余的,若H(d|B-a)>H(d|B),则B是独立的。若满足:(1)H(d|B)=H(d|A);(2)∨a∈B∶H(d|B-a)<H(d|B),则称B是A的属性约简。
下节将利用上述度量,构造混合数据间的模糊等价关系,依据属性重要性的度量进行约简。
2 模糊等价矩阵的构造及算法描述
基于模糊等价关系的数据构造是混合数据分析的重要模型,利用矩阵形式刻画具有不同属性类别的样本间关系。针对符号型属性,Hu[16]根据属性取值是否相等计算样本间的相似度贡献,属性间取其交集得结果,由此矩阵中只见两个单一数值,不能具体地刻画样本间的区分信息,且需针对每个属性做重复计算;刻画不同类别属性间的关系依然采用取其交集的简便算法,在各种属性类别取值丰富多样的信息空间,这种关系构造方法丢失大量的非冗余的有效信息。本节将对混合数据中各个类别属性分别重新进行构造,提出一种带权的对象间相似性度量方法,并且使其最终转化为一个模糊等价关系,在加入量化知识的基础上进行约简。
2.1 模糊相似关系的构造
给定一个包含n个样本的决策系统<U,A,D>,其中A=A1∪A2,A1定义为符号型属性的集合,A2定义为数值型属性的集合,U={x1,x2,…,xn},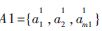 ,
,![54V6LDPS~C%NV77]SV@HM8N.jpg 54V6LDPS~C%NV77]SV@HM8N.jpg](http://files.chinaaet.com/images/2016/02/24/6359192996331800008105332.jpg) 。本节将描述样本的属性分类处理,分别定义与之对应的唯一函数。
。本节将描述样本的属性分类处理,分别定义与之对应的唯一函数。
符号型属性的取值是离散的、非有序的,若两个样本的条件属性取值完全相同,则其决策是一致的。因此,不同样本间的区分能力由取值不同的属性来体现,在此引入一个关系矩阵来体现符号型属性集对样本间的贡献度。

数值型属性的取值是连续的、有序的,当两个样本除属性a之外的其余条件属性相同时,针对属性a,若样本x比样本y占优,则x的决策至少不比y差。因此,不同样本间的区分能力由决策不一致的程度(即样本x比样本y占优的程度)来体现。同样定义数值型属性集对样本间的贡献度:

s(xi,xj)表示对象xi比xj在属性a上偏好、占优的程度,若xi比xj占优,则s(xi,xj)>0.5。若xj比xi占优,则s(xi,xj)<0.5。当s(xi,xj)=1时,说明xi比xj绝对占优。矩阵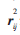 是s(xi,xj)转化后的对象间模糊相似关系,表示对象xi和xj间的相似性度量。
是s(xi,xj)转化后的对象间模糊相似关系,表示对象xi和xj间的相似性度量。
以上是针对一个数值属性进行的对象间模糊相似处理,对于多个属性,采用交运算来归并不同属性间的模糊关系。假设属性a和属性b分别计算其偏好关系为wij和zij,则对象xi与xj对属性{a}∪{b}量化的偏好关系为min(wij,zij)。

以上论述中提出了带权的对象间相似性度量方法,实现了混合数据间的模糊相似关系构造,但模糊等价关系是计算信息熵的前提,因此,最后还需将模糊相似矩阵转化为模糊等价矩阵。
2.2 模糊等价关系的构造算法及约简算法
本节采用Lee Hauan-Shih给出的关于模糊相似矩阵传递闭包问题的优化算法来进行转化[19],使其满足模糊等价关系的充要条件传递性,具体算法如下:
算法:设模糊相似矩阵为R=(rij)n×n,模糊等价矩阵为R*=(r*ij)n×n
输入:R=(rij)n×n
输出:R的传递闭包R*
(1)令r*ii=1(1≤i≤n);
(2)集合U={rij|j>i}中的元素是从大到小排序的序列;
(3)
①若R*中元素不存在r*ii=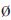 ,结束算法;否则转步骤②。
,结束算法;否则转步骤②。
②对于U中的最大元素ri′j′,若r*i′j′=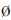 ,令I={j|r*i′j≠
,令I={j|r*i′j≠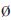 },J={i|r*ij′≠
},J={i|r*ij′≠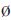 },置r*ij=r*ji=ri′j′(i∈I,j∈J),U=U-{ri′′j};否则,转步骤①。
},置r*ij=r*ji=ri′j′(i∈I,j∈J),U=U-{ri′′j};否则,转步骤①。
下面将采用基于属性重要性的约简算法进行约简,算法中设置一个信息表T用来存储所有属性值,其中属性元素按照领域专家的经验值和用户的需求偏好多寡来排序。
算法如下:
输入:决策系统S=<U,A,V,f>,A=C∪d,信息表T;
输入:S的属性约简RED。
(1)令RED=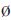 ;
;
(2)令T中元素从大到小进行排序;
(3)
①选择T中第一个属性ai,计算H(d|ai∪RED)以及SIGi(ai,ai∪RED,d)=H(d|RED)-H(d|ai∪RED)
②若SIGi>0,则ai∪RED→RED,T-ai→T,返回
步骤①;否则算法结束。
3 实验分析
本节在MATLAB实验环境下选择UCI数据库中的数据集,验证混合数据的模糊等价关系构造约简方法的有效性,表1列出了数据集的基本信息。可以看出其中数据集WPBC包含一类属性,其他数据集包含两类属性。
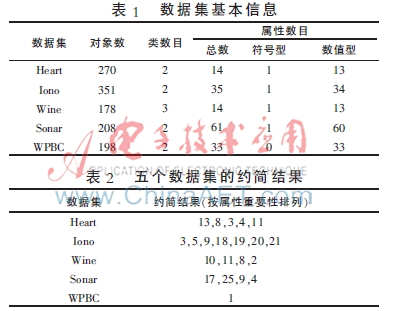
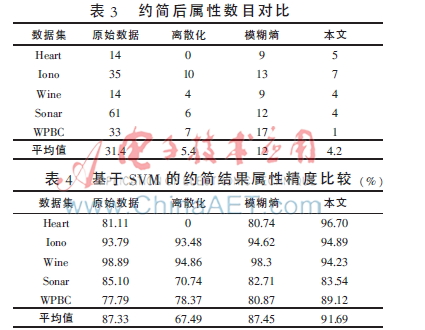
表2和表3分别列出了本文方法下的数据集约简结果以及约简后属性数目的统计。
分析表3,与其他三种方法(原始数据下的约简、离散化方法下的约简、模糊熵方法下的约简)[16]支撑的数据相比,本文方法在信息量保持不变的前提下剔除了更多的冗余属性;同时,针对包含一类或两类属性的数据集都进行了有效的约简。表4是采用支持向量机对本文结果与其他几种方法[16]的约简数据进行精度对比。实验结果显示本文方法下约简后的属性精度平均值较高。由此可以看出本文提出的基于模糊等价关系构造的混合数据约简有效地达到了约简的目的,并且得到较优的约简结果。
4 结束语
模糊粗糙集和粗糙模糊集概念的提出,融合了模糊粒化和粗糙逼近两种不确定性方法,基于模糊粗糙集模型构建模糊等价关系是混合数据分析的有效方法之一。针对混合型信息系统,本文分别提出各类数据的对象间度量以及总体度量方法,建立带权的对象间相似性度量方法,在转化为模糊等价关系的基础上,采用了加入领域专家的经验知识和系统客户需求的约简算法。通过实验数据分析验证了方法的有效性和可行性。
参考文献
[1] PAWLAK Z. Rough sets-theoretical aspects of reasoning about data[M]. Dordrecht: Kluwer Academic, 1991.
[2] 张清华,王国胤,肖雨.粗糙集的近似集[J].软件学报,2012,23(7):1745-1759.
[3] 石梦婷,刘文奇,余高锋,等.变精度软粗糙集[J].计算机工程与应用,2014(1):101-104.
[4] CATLETT J. On changing continuous attributes into ordered discrete attributes[C]. European working session on learning, 1991:164-178.
[5] LIU H, HUSSIANM F, TAN C L, et al. Discretization: an enabling technique[J]. Data Mining and Knowledge Discovery, 2002,6(4):393-423.
[6] HALL M A. Correlation-based feature selection for discrete and numeric class machine learning[C]. In Proc 17th ICML, 2000:359-366.
[7] ZHOU Z H, QIAN C Z. Hybrid decision tree[J]. Knowledge Based Systems, 2002,15(8):515-528.
[8] TANG W. Y, MAO K. Z. Feature selection algorithm for mixed data with both nominal and continuous features[J]. Pattern Recognition Letters, 2007,28(5):563-571.
[9] KWAK N, CHOI C H. Input feature selection by mutual information based on parzen window[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002,24(12): 1667-1671.
[10] ZADEH L. Toward a generalized theory of uncertainty-an outline[J]. Information Science, 2005,172:1-40.
[11] DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J]. International Journal of General Systems, 1990,17(2-3):191-209.
[12] 范成礼,邢清华,邹志刚,等.基于直觉模糊粗糙集相似度的多属性决策方法[J].计算机工程与应用,2014(7):121-124.
[13] 丁世飞,朱红,许新征,等.基于熵的模糊信息测度研究[J].计算机学报,2012,35(4):796-801.
[14] Pan Zhenghua, Zhang Lijuan. A new fuzzy set with three kinds of negations and applications to decision making in financial investment[J]. Journal of Haman and Ecological Risk Assessment, 2011,17(4):795-780.
[15] 潘正华.模糊知识的三种否定及其集合基础[J].计算机学报,2012,35(7):1421-1428.
[16] Hu Qinghua, Yu Daren, Xie Zongxia. Information-preserving hybrid data reduction based on fuzzy-rough techniques[J]. Pattern Recognition Letters, 2006,27(5):414-423.
[17] HASHMI K, ALHOSBAN A, MALIK Z, et al. WebNeg: a genetic algorithm based approach for service negotiation[C]. In: Foster I, et al., eds. Proc. of the ICWS 2011, Los Alamitos: IEEE CS, 2011:105-112.
[18] 梁亚澜,聂长海.覆盖表生成的遗传算法配置参数优化[J].计算机学报,2012,35(7):1522-1538.
[19] LEE H S. An optimal algorithm for computing the max-min transitive closure of a fuzzy similarity matrix[J]. Fuzzy Sets and Systems, 2011,123(1),129-136.

