摘  要： 提出了一种直接序列扩频信号（Direct Sequence Spread Spectrum，DS-SS）的盲同步算法，该算法采用自相关矩阵的谱范数进行失步点估计，简单有效、误差小。理论分析及计算机仿真结果表明，该算法在低信噪比条件下可实现DS-SS信号的盲同步，进而可用于对直扩信号的参数估计。

　　关键词： 盲同步；直接序列扩频信号；伪随机序列

0 引言

　　直接序列扩频信号（DS-SS）由于具有一系列独特的优点，比如抗噪声、抗干扰、抗多径衰落、能在低功率谱密度下工作、有保密性、可多址复用和任意选址、测量精度高等，目前已经被广泛应用于军事通信、卫星导航等系统中。在非协作通信系统中，与之对应的信息侦测技术，尤其是直扩信号的盲估计成为目前研究的热点，参考文献[1-2]对DS-SS信号盲解扩方法进行了探讨。

　　实现信号的盲估计需要事先完成信号的盲同步。为了检测接收信号的起点，参考文献[3]提出一种基于协方差矩阵Frobenius范数最大化的盲同步方法，在低信噪比条件下具有优越的估计性能，然而其计算复杂度较大，特别是在扩频波形周期较大情况下性能下降严重。本文提出一种利用矩阵谱范数的直扩信号盲同步方法，能够比Frobenius范数法进一步提高同步估计精度。

　　1 DS-SS信号模型

　　假设接收信号为扩频周期已知的基带直扩信号，并且被白噪声污染，可表示为：

　　其中，ak为相互独立且等概率随机分布的信息码序列，码元宽度为Ts；n（t）为零均值加性高斯白噪声；h（t）为扩频波形，它是一个完整周期的扩频序列基带信号与传输链路的等效传递函数的卷积：

　　其中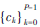，为扩频码序列，码元宽度为Tc，P为扩频码长且有P=Ts/Tc；p（t）代表发射、信道冲击响应以及接收滤波器的综合卷积。

　　不失一般性，本文做如下假设：信息序列为均匀分布且互不相关；噪声为零均值高斯白噪声，且与信号不相关。

2 基于谱范数的盲同步方法

　　假设信息码时宽Ts已经利用已有方法估计得到，例如可用参考文献[4]的方法，因此可假设Ts为已知。设采样率为Te，接收的信号经采样后得到的信号矢量记作y：

　　y=[s（0），s（Te），…，s（（j-1）Te）]（3）

　　其中j=1，2，…

　　现在目的是寻找y中对应的第一个信息码的采样点，具体方法如下：将数据划分为N个互不重叠的数据段，每个数据段长度为Ts，也可认为是在信号中加入N个宽度为Ts的相邻分析窗。每个分析窗中包含M个采样点，即Ts=MTe。

　　设数据的失步时间t0为d个采样周期，即t0=d×Te，d∈[0，M-1]，观察第k个分析窗，该窗内数据可用M维矢量yd，k表示为：

　　yd，k=[s（（d+（k-1）M+1）Ts），…，s（（d+kM）Ts）]（4）

　　在此基础上，将N段数据按顺序作为列向量，构造M×N阶矩阵：

　　Y=[yd，1，…，yd，N]（5）

　　为降低噪声的影响，采用Y的自相关矩阵进行分析，该自相关矩阵为：

　　R=E{YYH}（6）

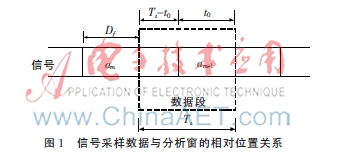
　　图1给出了同步前接收信号与数据分析窗之间的位置关系，其中t0为分析窗与信息码符号起始位置之间的时间差。同步的目的是通过改变分析窗的位置，使得分析窗位于信息码的起始位置，以便于对信号的后续处理。

　　实际应用中计算R的常用方法是计算其估计值[5]，。

　　参考文献[4]指出，当的特征值λ1最大时，意味着信号的失步时间为0。因此估计失步时间相当于寻找使得特征值λ1最大的自相关矩阵。而当λ1最大时，的Frobenius范数的平方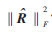达到最大值，‖·‖F表示矩阵的Frobenius范数。参考文献[3]正是通过移动分析窗使得 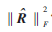最大，从而使得分析窗位于信号的起始点，从而实现同步。

　　根据矩阵理论[6]，在有噪声扰动的情况下，对于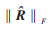，扰动产生的误差下界为P2，显然当扩频码长度P较长时，误差将明显增大，同步点位置估计性能会显著下降。因此本文采用其他方法来估计失步时间。

　　在矩阵理论中，另一常用的算子范数为谱范数，表示为‖·‖2，谱范数计算方法为求矩阵的最大特征值。对于，λi表示矩阵的特征值。在受同样噪声扰动的情况下，对于谱范数‖‖2，扰动产生的误差下界为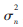，明显小于Frobenius范数。因此本文使用的谱范数来寻找信息码的起点。显然，当移动分析窗使得信号达到同步时，其自相关矩阵的谱范数也会达到最大。综上所述，本文对失步点d的估计方法为：

　　如果事先得到的是信码宽度的粗糙估计值，本算法在以该粗糙估计值为中心的某一邻域内还可进一步对失步点进行精确估计，此处不再详述，由计算机仿真可以得到验证。

3 仿真实验

　　为了验证算法的有效性，本文利用MATLAB软件进行计算机仿真。采用31位m序列作为PN码序列，信噪比SNR=-10 dB。假设采样频率为1 MHz，即Te=1 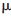s，且每个PN码码片含有2个采样点：Te=Tc/2，失步时间t0=23Te。

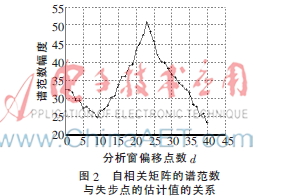
　　图2给出了该信号分析窗内数据的自相关矩阵的谱范数与分析窗偏移点数的关系，从图中可见当分析窗偏移点数为23时，谱范数取得最大值，因此失步点的估计值为23。

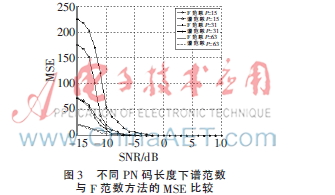
　　图3针对不同PN码长的信号，给出了其谱范数与Frobenius范数的最小均方误差（MSE）随信噪比变化的情况。可以看出，在同样的码长与信噪比下，本文方法比Frobenius范数误差小，并且PN码越长优势越明显，这也验证了本文的理论分析。

4 结论

　　本文主要讨论了DS-SS信号的盲同步问题。由理论分析及计算机仿真可知，本文提出的盲同步算法在低信噪比情况下，可以有效地实现DS-SS信号的盲同步，并可在此基础上估计出信号的其他参数。相比于已有的算法，该算法简单、误差小，低信噪比下性能更优越，不足之处在于求最大特征值的运算量较大，这也是本文今后改进的方向。

参考文献

　　[1] 王满喜，李宏，马刈非，等.非周期性DSSS信号的PN码序列盲估计[J].信号处理，2009，25（10）：1605-1611.

　　[2] 詹亚峰，曹志刚，马正新.DSSS信号的扩频序列估计[J].电子与信息学报，2005，27（2）：169-172.

　　[3] BOUDER C， AZOU S， BUREL G. A robust synchronization procedure for blind estimation of the symbol period and the timing offset in spread spectrum transmissions[C]. IEEE Seventh International Symposium on Spread Spectrum Techniques and Applications， Prague， 2002：238-241.

　　[4] BUREL G. Detection of spread spectrum transmissions using uctuations of correlation estimators[C]. IEEE Int. Symp. on Intelligent Signal Processing and Comm. Systems， Hawai， 2000：5-8.

　　[5] 张天琪，李立忠，张刚，等.直扩信号的盲处理[M].北京：国防工业出版社，2012.

　　[6] 陈景良，陈向辉.特殊矩阵[M].北京：清华大学出版社，2001.