摘  要： 针对雷达的目标检测概率和跟踪精度随着目标距离的增大而降低的问题，提出了一种基于门限体积最小准则的认知雷达的波形选择方法。该方法在高斯噪声、线性运动目标跟踪方法的基础上，通过测量噪声与发射波形之间的关系，在经典卡尔曼滤波算法的框架中增加了波形选择模块，来实现对跟踪波形的调节。仿真结果表明，该方法能够明显地提高雷达的跟踪性能。

　　关键词： 认知雷达；卡尔曼滤波；门限体积最小准则

0 引言

　　随着社会与科技的快速发展，无论是航海或是航空，交通愈加繁忙。为了避免海上或是空中交通事故，更早、更准确地发现对方船只或飞机，人们对于雷达的检测能力和检测精度有了更高的要求。但只能发射固定波形的传统雷达，由于探测目标所处环境的复杂性，很难满足现代人们的需求。于是，2006年，加拿大麦克马斯特大学（McMaster University）国际著名信号处理专家Simon Haykin教授第一次提出了认知雷达的概念[1]，并对认知雷达的功能及各个组成部分做了详细说明。认知雷达能够通过对环境和目标的特征进行分析，从而对信号智能处理，根据探测目的选择相应的发射波形，提高雷达的检测能力和精度。Guerci[2]和Wicks[3]也分别在2010年IEEE国际雷达会议和认知雷达信号处理国际研讨会上从不同角度阐释对认知雷达的看法及其所需的相关技术。

　　对于雷达波形选择技术的研究，Kershaw和Evans[4]于1994年首次在传统的雷达目标跟踪系统中增加了波形自适应选择模块。他们在声呐系统中将发射波形参数引进测量噪声协方差，从而建立了发射波形与跟踪算法之间的关系，通过计算最小化估计误差来得到最优波形选择方法。Simon Haykin于2010年进一步提出了基于容积Kalman滤波[5]的认知跟踪雷达的概念，以及预测跟踪误差最小化的最优波形选择准则[6]，在经典弹道目标跟踪的仿真中，论证了认知跟踪雷达相较于只能发射固定波形的传统雷达的优势。东北大学的王彬[7]针对雷达目标转移概率未知的特点，把自适应波形选择问题建模为随机动态规划模型，提出应用Q学习的方法进行波形选择。北京装备学院的俞道滨[8]在基于波形库的目标跟踪波形选择方法上也做了论证，得出了不同的波形选择准则能够根据需求提高雷达跟踪的精确度和准确性的结论。

1 认知雷达波形选择的系统框图

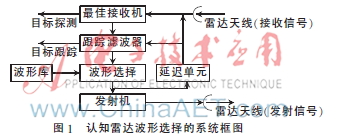
　　认知雷达波形选择的系统框图如图1所示。在传统的雷达目标探测及跟踪过程中，没有发射波形选择的模块。波形选择模块通过预测协方差选择下一时刻的发射波形，发射波形不同，测量噪声方差的Cramer-Rao下限（CRLB）也不同，从而对测量方程产生影响[9]。

　　2 信号模型

　　通常雷达发射的波形sT（t）为[1]：

　　式（3）中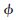，为随机相移，ER为接收信号的能量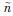，（t）为零均值的高斯白噪声，它的频谱密度为N0/2，参数τ0和v0分别为目标的时延和Doppler频移。在对运动目标进行跟踪时，通过对发射和接收信号的分析，可以实时获取目标的距离和速度等信息。

3 跟踪滤波算法

　　本文提出的目标模型是在无杂波、高斯噪声环境中做线性运动的条件下的构造。在此情况下，卡尔曼滤波就是最优的贝叶斯滤波器[10]。

　　设专为波形参数的可选集合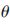，k为k时刻的发射波形，则测量噪声协方差为N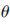（k），由卡尔曼滤波可知，测量信息协方差为：

　　在已知目标的初始状态及其运动模型等条件时，经以上几个方程式交替循环计算，可获得目标状态和量测的更新值，实现对目标的跟踪。

4 波形选择准则及最优化方案

　　波形选择准则是下一时刻发射什么样的波形的依据，它与跟踪的目的紧密相关，不同的跟踪目的将有不同的波形选择准则。本文从使跟踪k时刻测量空间的体积最小，减少在高密度杂波下的虚假测量数或者高噪声情况下的测量误差的角度考量，采用门限体积最小准则。其表达式为：

　　式（10）在参考文献[2]中有详细的推导过程。

　　波形最优化方案则是下一时刻选择发射波形的方式。波形最优化方案主要包括波形设计和波形选择。波形设计主要是利用动态变化环境来设计波形，其主要缺点是实时性较差，因而在雷达中几乎很少采用。波形选择则需在雷达工作前设计好一组波形或波形参数，建立波形库。雷达工作时，根据波形选择准则在波形库内选择最优的波形。随着大容量存储器及高速率处理器的发展，波形选择具有更高的可实现性，故本文波形最优化方案采用的是波形选择。如图2所示，一般波形库会采用多种不同的波形。而本文只采用3种典型的雷达信号波形，在跟踪不同距离、不同速度的目标时具有各自的特点。根据雷达性能的需求，调用最优的波形。

5 仿真实验及结果分析

　　本文仿真实验中采用的三种信号波形的函数表达式分别为：

　　三角脉冲信号：

　　三角脉冲信号的有效脉冲宽度为2λ，高斯调制脉冲信号和高斯调制线性调频信号的脉冲宽度为7.433 8λ。对于三角脉冲信号和高斯调制脉冲信号只能进行脉宽调制，而对高斯调制线性调频信号的脉宽和调频率都可调制。

　　仿真实验的环境相关参数及目标的初始状态：

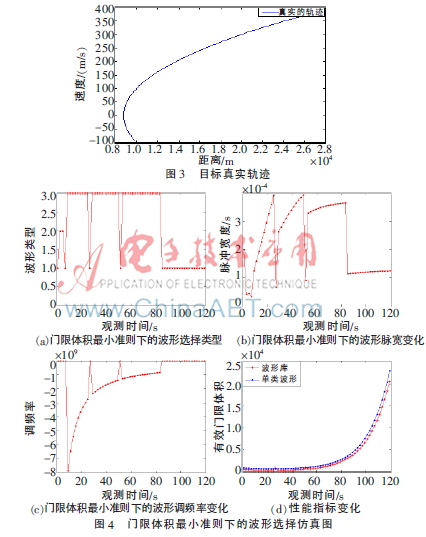
　　假设使用一座距离-速度同时观测的雷达平台对一目标进行观测跟踪，此目标先靠近该平台运动再远离该平台运动。设远离平台方向为正，靠近平台方向为负。如图3所示为目标的距离和速度轨迹。该目标初始距离r为10 000 m，速度为-100 m/s，加速度为4 m/s2。观测值为距离和速度，观测间隔t=2 s，观测时长120 s。雷达跟踪系统模型中的参数为：

　　目标跟踪的初始协方差矩阵为：

　　过程噪声方差Q=0.000 1。设雷达的有效观测距离为200 km，则信噪比可以表示为：

　　SNR=（200 000/s）4（14）

　　式中，s表示目标到雷达的距离。初始波形选为三角脉冲，其初始脉冲宽度为λ=100 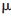s，脉冲宽度参数变化范围为30~400 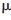s，调频参数b变化范围为-10×109~10×109。与之相对比的传统雷达，采用高斯调制调频单类波形。其固定发射脉宽λ=5×10-7 s，调频参数b=5×109。在门限体积最小准则下，经过500次蒙特卡罗仿真运算，得到其仿真结果如图4所示。

　　由仿真结果图4可知，在跟踪目标距离雷达观测平台较近时，认知雷达根据门限体积最小准则选用的是高斯调制线性调频信号，使跟踪目标的门限体积保持在较小的范围内。在跟踪过程中，调频率逐渐增大，以保持在跟踪过程中测量空间的体积较小。而在跟踪目标距离雷达观测平台较远时，认知雷达选用的是三角脉冲，使跟踪目标的门限体积明显小于无波形库的情况，能够有效地提高雷达远距离的探测精度。其中的波形脉冲脉宽变化和调频率图像的陡然落差，主要是由于波形库中波形的脉宽限制所造成的。

6 结束语

　　本文研究了与传统跟踪雷达相比能够自适应选择发射波形的认知雷达，其在无杂波、高斯白噪声及跟踪目标做线性运动的情况下，根据门限体积最小准则从建立的波形库中选择最优发射波形。通过与传统跟踪雷达对比可知，认知雷达的跟踪性能的确得到了显著提升。

　　参考文献

　　[1] HAYKIN S． Cognitive radar： a way of the future[J]. IEEE Signal Processing Magazine，2006，23（1）：30-40.

　　[2] GUERCI J R.Cognitive radar： a knowledge-aided fully adaptive approach[C]． Processings of IEEE Radar Conference， Washington DC， IEEE Press，2010：1365-1370.

　　[3] WICKS M． Spectrum crowding and cognitive radar[C]． 2nd International Workshop on Cognitive Information Processing，IEEE Press，2010：452-457.

　　[4] KERSHAW D J，EVANS R J． Optimal waveform selection for tracking systems[J]． IEEE Transactions on Information Theory， 1994，40（5）：1536-1550．

　　[5] ARASARATNAM I ， HAYKIN S. Cubature Kalman filters[C]. IEEE Transaction on Automatic Control， 2010：1254-1269.

　　[6] HAYKIN S. Cognitive tracking radar[C]. IEEE Radar Conference， 2010：1467-1470.

　　[7] 王彬，汪晋宽，宋昕．认知雷达中基于Q学习的自适应波形选择算法[J]．系统工程与电子技术，2011，33（5）：1007-1011．

　　[8] 俞道滨，吴彦鸿，朱卫纲．基于波形库的目标跟踪波形选择方法研究[J]．雷达与对抗，2013，33（2）：35-39．

　　[9] 夏洪恩．基于目标跟踪的波形自适应选择技术[D]．长沙：国防科技大学，2010．

　　[10] 何友，修建娟，关欣，等．雷达数据处理及应用（第三版）[M]．北京：电子工业出版社，2013．