文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.02.003
中文引用格式: 贺江,蒲宇亮,李海波,等. 一种基于OpenCL的高能效并行KNN算法及其GPU验证[J].电子技术应用,2016,42(2):14-16.
英文引用格式: He Jiang,Pu Yuliang,Li Haibo,et al. A energy efficient parallel KNN algorithm evaluated on GPU using OpenCL[J].Application of Electronic Technique,2016,42(2):14-16.
0 引言
近年来,许多不同类型的处理器广泛应用于高性能计算领域,如GPU、FPGA、DSP等[1],而异构计算平台由不同类型的处理器组成,能对许多不同的算法进行加速实现。OpenCL是一种开放式的异构计算标准,支持异构系统的并行程序应用。作为经典聚类算法,KNN在文字识别、预测分析、图像处理和图像识别等方面[2]有非常重要的应用。
为了加速KNN算法的实现,许多文章也提出了一些新的思路。Zhang Hao等[3]通过结合支持向量机(SVM)和KNN算法实现视觉分类识别。Garcia等[4]提出一种基于插入排序的快速KNN算法实现,并分析了奇偶排序和插入排序的性能。2009年,Liang Shenshen等人[5]提出了基于CUDA实现的并行KNN算法,称该算法为CUKNN。该算法通过调用大量GPU线程,在计算待分类数据和参考数据集时高度并化,然后对距离进行并行排序。
基于CPU+GPU的异构计算系统最近几年在算法加速方面得到了广泛使用,如神经网络[6]、数据挖掘[7]等。而基于CPU+FPGA系统由于其能效优势[8],得到业界的认可。
本文提出了一种基于CPU+GPU异构计算系统的KNN并行算法。该方法将待分类的数据集通过并行冒泡的方法进行分类,称该方法为PBKNN(parallel sort)。
1 KNN算法与OpenCL架构
1.1 KNN算法
KNN分类算法实现简单,分类错误率低,其实现通常分为三步:距离计算、距离排序、分类判决。
距离计算是计算待分类数据和参考数据集数据之间的距离,本文采用的是欧式距离。
算出待分类数据与每个参考数据集样本之间的距离之后,需选出其中最小的K个距离,作为判决的标准。针对如何从多个数据中选取K个最小的数据,提出了一种新的并行冒泡排序方法,该方法无冗余计算且可并行实现。并行冒泡排序也曾被提出来加速排序的计算速度,如奇偶冒泡排序[9],但该算法由于大量冗余计算,实现时性能不佳。本文提出的并行冒泡排序只需要K个气泡来选取K个最小的数据,如图1所示。

1.2 OpenCL架构
OpenCL程序在主机和设备上执行,支持基于数据和基于任务的并行编程模型。图2是有主机的多个设备组成的OpenCL平台模型[10]。

执行内核程序时,OpenCL将定义一个索引来执行该内核的实例,该实例就是OpenCL的工作项,每个工作项执行的代码相同。工作项的内存称作私有内存。一些特定的工作项组成工作组,相同工作组共享局部内存,相同工作组中的不同工作项在不同计算单元上并行运行。
本文采用通用图形处理器(GPGPU)来作为异构系统的计算设备,由于GPU拥有大量的计算核心,其浮点计算效率远高于CPU,所以GPU作为OpenCL的通用计算设备拥有很高的计算效率。
2 并行冒泡的KNN算法实现
2.1 距离计算内核
距离计算内核计算每个待分类数据到每个参考数据集样本之间的距离,每次距离计算由一个工作项完成。数据集由CPU传输到GPU的全局内存,相应工作组的数据由GPU全局内存传输到GPU局部内存,以此充分利用局部内存的带宽,提高GPU计算核心的数据访存速度。距离计算如图3所示。

2.2 距离分组排序内核
为了充分利用GPU的计算资源,提高计算的并行度,将得到的待分类数据和参考数据集的所有距离进行排序时,先将距离分组,若分组数为N,通过并行冒泡选取每组数据最小的K个距离,得到N×K个距离。一个待分类数据共有N个工作组进行分组排序。
每个工作组通过并行冒泡进行排序,一个工作组拥有K个工作项,每个工作项对比相邻的两个数据,K个工作项从数据的起始端一直对比到数据的末端,从而选出最小的K个距离。第1个周期时,共一个工作项进行第1个和第2个距离进行比较;第2个周期时,第1个气泡比较第3个和第4个距离,第2个数据比较第1个和第2个距离,直到N个工作项产生N个气泡。气泡数目稳定后,经过若干个周期,K个气泡便可以同时携带K个最小的距离。所以该过程共有2个过程,气泡增加,气泡稳定。具体过程如图4、图5所示。

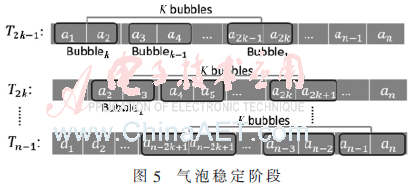
2.3 距离计算内核
在分组内核中,每个待分类数据共得到M×K个距离,该内核就是从这M×K个数据中选出K个最小的数据。由于参考数据集很大,这个内核消耗的计算时间相比分组排序只占小部分。
3 结果分析
3.1 算法性能分析
为了让距离分组内核得到合理的分组数目,通过设置不同的分组数目,得到在GPU上计算消耗的时间。实验中,采用英特尔处理器i7-3770K作为OpenCL主机,AMD Radeon HD7950作为OpenCL设备。该CPU是4核处理器,主频3.5 GHz,24 GB内存。该GPU拥有28个计算单元,最大工作频率为900 MHz,3 GB GDDR5内存,内存带宽为240 GB/s。所有实验数据由MATLAB产生,参考数据集为10 240×8个浮点数据,每个数据共64维,K为16,待分类数据个数为32。
为了找到每个待分类数据距离的最佳分组数,将每个待分类数据10 240×8个参考数据集的距离进行分组,将分组数分别设置为4×8,8×8,直至48×8。通过实验,记录每次实验的GPU时间消耗,如图6所示。

当分组数较小时,分组排序内核随着分组数的变大,时间消耗迅速下降;当分组数变大后,时间消耗趋于稳定。因为当分组数较小时,每个工作项的计算量和数据传输量过大,且GPU的计算资源没有充分利用;当分组数变大后,GPU计算资源得到充分利用,但工作组和工作项的数目也会随之变大,从而导致额外的控制开销。根据实验数据,将分组数设定为32。
本次实验,把CUKNN和PBKNN进行OpenCL实现时,工作组大小均设置为256。CUKNN进行排序时,每个工作组将浪费(256-K)/256×100%的时间计算无关数据的排序。而PBKNN对此进行优化,避免了无关数据的排序。所以,理论上来说,PBKNN的时间消耗是CUKNN的K/256。
3.2 实验验证
PBKNN和CUKNN采用相同的数据和相同的实验环境。参考数据集中数据点个数从1×10 240到64×10 240变化,如表1。对于PBKNN,共有256个工作组,每个工作组共有64个工作项;对于CUKNN,工作组数目分别设置为40,80,120,…,320,其每个工作组的工作项数目最大时,性能最好。所以每个工作组的工作项的数目设置为256。
BPKNN和CUKNN均通过三个内核实现KNN算法。由于第一个和第三个内核的时间消耗较少,主要对比第二个内核的时间消耗。实验结果如表1。
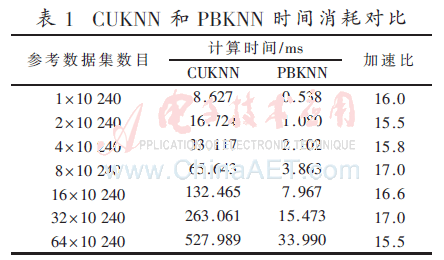
从实验结果可以看出,在相同的实现平台上通过减少无关数据的排序,PBKNN相比于CUKNN计算时间大幅减少,因而对应的能量效率也得到了很大的提升。
4 结论
本文提出了一种基于CPU+GPU的异构计算架构的并行冒泡KNN算法—PBKNN算法,该算法充分利用了GPU的并行计算能力及OpenCL的编程优化。通过在AMD Radeon HD GPU实测,PBKNN在关键排序时间仅为CUKNN的1/16,因而极大地提升了处理速度和计算能效。
参考文献
[1] Khronos group.The open standard for parallel programming of heterogeneous systems[EB/OL].http://www.khronos.org/opencl/.
[2] PENG Y,KOU G,SHI Y,et al.A descriptive framework for the field of data mining and knowledge discovery[J].Int.J.Inf.Technol.Decis.Mak.,2008,7(4):639-682.
[3] ZHANG H,BERG A C,MAIRE M,et al.SVM-KNN:discriminative nearest neighbor classification for visual category recognition[C].In International Conference on Computer Vision and Pattern Recognition,New York(NY),USA,2006.
[4] GARCIA V,DEBREUVE E,BARLAUD M.Fast k nearest neighbor search using GPU[C].In:IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops(CVPRW′08),2008:1-6.
[5] LIANG S,WANG C,LIU Y,et al.CUKNN:a parallel implementation of knearest neighbor on cuda enabled GPU[C].In:IEEE Youth Conference on Information,Computing and Telecommunication(YC-ICT′09),2009:415-418.
[6] HOFFMANN J,EI-LAITHY K,G?譈TTLER F,et al.Simulating biological-inspired spiking neural networks with OpenCL[C].ICANN 2010,Part I,LNCS 6352,2010:184-187.
[7] CHE S,BOYER M,MENG J Y,et al.A performance study of general purpose applications on graphics processors[J].Journal of Parallel and Distributed Computing,2008,68(10):137-1380.
[8] BALEVIC A,ROCKSTROH L,LI W,et al.Acceleration of a finite-difference time-domain method with general purpose GPUs(GPGPUs)[C].Proc.of International Conference on Computer and Information Technology,2008,1-2:291-294.
[9] PETERS H,SCHULZ-HILDEBRANDT O,LUTTENBERGER N.A novel sorting algorithm for many-core architectures based on adaptive bitonic sort[C].In:Parallel & Distributed Processing Symposium(IPDPS),2012 IEEE 26th International,2012.
[10] GROUP K O W.The opencl specification[EB/OL].(2011)[2015].http://www.khronos.org/registry/cl/specs/opencl-1.1.pdf.

