0 引言

    高频化、大功率化和集成化是绝缘栅双极型晶体管(IGBT)不断发展的方向^[1]。功率和集成度的增加使得IGBT所承受的功率密度不断升高，同时随着技术的不断发展IGBT工作的频率也不断增大，这些都使器件的发热问题愈加严重。IGBT各层材料的厚度、热膨胀系数、热导率、热阻值和热容值各不相同，在温度梯度与热应力的反复冲击下，焊料层之间产生的剪切应力导致薄弱处将逐渐产生细微的裂纹。裂纹的不断增加会减小硅芯片热量传导和焊料层的有效传热面积，导致其平均温度升高，加速空洞的产生和封装热阻的增加^[2]。风电系统的运行过程中，服役期内运行周期T_o(in operation)和维修周期T_m(in maintaining)交替出现。如果能在维修周期中对模块的特性进行检测，从而估计它的健康状态以及仍可安全运行的时间，必然产生巨大的经济效益，并提高电网的安全运行。因此研究IGBT功率模块在热应力不断冲击过程中热阻的老化规律，并以此为依据对模块的健康状态进行评估，预测模块的剩余寿命具有十分重要的科学意义。

1 IGBT热疲劳形式分析

    IGBT器件的热疲劳现象通常分为两种形式，一种是功率循环模式，另一种是温度循环模式。功率循环加速老化方法通电时间短，冷却时间长，壳温T_c在一个温度冲击循环过程中的变化较小，而IGBT芯片的温度(T_j)波动剧烈，该方法主要用于模拟键合线老化失效^[3]。温度循环加速老化方法一次循环时间较长，较长的循环时间不仅使结温波动量ΔT_j较大，同时也使得壳温T_c的变化幅值差ΔT_c较大，该方法能同时模拟铝键合线和焊料层的老化失效^[4]。

    IGBT模块内部材料结构的退化必然导致外部电热参数出现一定变化，变化较为明显的是模块导通饱和压降和热阻。由于饱和压降测量较容易，多数文献研究饱和压降的退化规律^[5-7]，本文则利用定制的IGBT老化实验平台和热阻测试系统研究温度循环下IGBT热阻的退化规律。

2 实验原理和实验平台

2.1 试验方案

    正常工作情况下IGBT模块的寿命约为10年，在正常工作下研究其退化规律花费时间过长，因此考虑加速老化实验。如图1所示为加速老化实验的电路原理图，图中DUT为试验器件；PWR为程控试验电源(5 V，300 A)；V_G为G脚程控电压(0～15 V)；R_G为G脚串联电阻(10 Ω/2 W)；RIS为电流互感器(0～300 A)。

    具体实验过程如下：首先对全新的IGBT器件进行测试，用IGBT热阻测试平台测量IGBT器件温度系数、饱和压降及集电极电流，计算出热阻。然后对IGBT模块进行温度循环老化实验,壳温由40 ℃升温到90 ℃，再由90 ℃降温至40 ℃，此为一个温度循环，每循环1 000次后，再采用热阻测试系统测量IGBT器件温度系数、饱和压降及集电极电流，计算出热阻。重复以上步骤，直到模块老化失效，实验停止。

2.2 热阻测试平台

2.2.1 热阻测量的原理

    以结壳热阻为例，稳态热阻的定义式为：

式中，T_j为模块的结温，T_c为模块的壳温(铜底板温度)，P_loss为模块的平均功率损耗。

    壳温可以通过在器件底部放置温度传感器获得，功率损耗可以通过测量导通饱和电压和集电极电流计算得到。但结温是器件内部芯片上的最高结温，不易直接测量，因此采用热敏参数法获得器件的结温。小电流下半导体PN结电压随温度变化具有非常好的线性，用半导体器件结电压作为温敏参数，测量其工作条件下的变化，可以达到测量温升及热阻的目的。采用小电流下的IGBT集电极-发射极电压作为热敏参数的测量电路图如图2所示。

2.2.2 试验布骤

    试验分两步进行：

    (1)将IGBT模块置于控温箱中，同时将控温箱温度设置为T₁，通入测量电流I_M，测量此时的集射极电压V_CE1；再将温度设置为温度值T₂，测量温度T₂时的集射极电压V_CE2得到模块的温度系数：

    (2)将测试模块从控温箱中取出并固定在散热器上，测量此时模块的壳温T_c1，通入测量电流I_M来测试此时模块的集射极电压V_CE3。接着，对测试模块通以加热大电流I_C，当模块达到热平衡后测定此时的壳温T_C2以及集射极电压V_CE4。最后，断开开关K，切断加热大电流并闭合K₁通以小测试电流I_M，在极短时间内测量此时的集射极电压V_CE5。通过上述相关测量可以获取通以加热大电流后达到平衡时模块温度T_j的公式：

2.3 加速老化试验平台

    加速老化实验系统采用上位机控制方式。系统配置十个相对独立的老化实验区，每个老化实验区由加热电路(提供0~300 A直流电流)、驱动电路(提供0~20 V的驱动电压)和冷却系统(风机和散热器)组成(如图3所示)。其中①安装平台: 用于试验器件的固定与散热(中间带有温度探头);②风机：用于试验器件(包含散热器)的辅助风冷散热;③④：电源功率输出的正端和负端(提供加热电流)；⑤⑥：驱动电源的正负极(为IGBT提供驱动电压)。上位机可以实时显示每个实验区域的状态、循环次数、采样数、运行时间、每个循环的导通时间和断开时间、V_cesat、导通电流、壳温等。

3 实验结果分析

3.1 多项式模型理论分析

3.1.1 多项式模型拟合次数选择

    多项式拟合次数越高对已有点的描述越贴切，但如果拟合次数过高的话又会削弱数据的趋势性，因此需要选定最佳的拟合次数。

    设有n个成对的点x，y=(x₁，y₁)、(x₂，y₂)、(x₃，y₃)…(x_n，y_n)

    对这n个点进行多项式拟合，下标代表拟合多项式次数

3.1.2 多项式模型回归分析

    模型建立后需要对模型进行可信度检验，本文用方差分析检验多元回归模型的统计可信度。方差分析将因变量的变异分解成组内部分和组间部分，然后比较组间部分和组内部分的相对大小，据此来判断基于样本数据得到的回归模型是否真实反映总体的变化规律。具体公式如下：

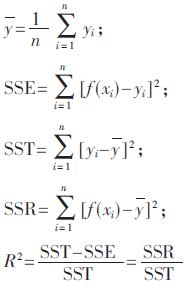
    其中：SST为残差平方和，SST为总平方和，SSR为回归平方和，R²为判定系数

    R²(0~1)反映趋势线的估计值与对应的实际数据之间的拟合程度，越接近1则说明趋势线的可靠程度就越高。

3.2 实例分析

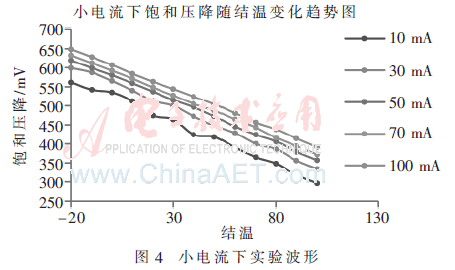
    实验中，首先将全新的IGBT模块放在调温调湿箱中做小电流测试实验，测量I_M分别为10 mA、30 mA、50 mA、100 mA时，IGBT模块在不同结温下的饱和压降U_(sat)ce。结温由恒温箱控制，使恒温箱在某一温度下保持足够长的时间，此时IGBT结温等于环境温度，且测试电流足够小，模块在测量过程中不自热，认为结温始终等于恒温箱设定温度。使恒温箱的温度从-20 ℃～100 ℃变化，每隔10 ℃测量一次。实验结果如图4所示，可以看出IGBT饱和压降随结温基本成线性关系，其中测试电流为100 mA时线性度最好，因此选择100 mA作为测量温度系数的测试电流。

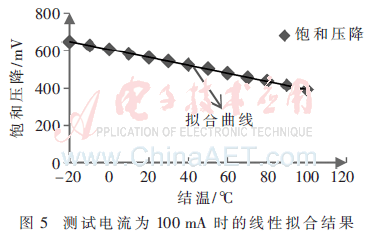
    对100 mA下的测量结果进行线性拟合，拟合结果如图5所示，得到温度系数α=2.130 8，通过式(4)可以得到IGBT的初始热阻为0.15 ℃/W。将IGBT模块放入老化设备中，每经过1 000次温度循环，测量模块在100 mA下的温度系数，并计算得到的热阻，直到器件失效为止。图6为温度循环下IGBT热阻及其偏移量的波形。

    由图可知，随着热应力的不断冲击，IGBT的性能发生了一定程度的退化，热阻随着温度循环次数的增多不断增大。

    通过对数据进行分析发现热阻增量符合多项式模型，对热阻增量进行不同次数的多项式拟合，并用上述拟合次数选择标准进行判断，发现热阻退化量最佳拟合模型为四次多项式模型（拟合曲线如图7所示）。

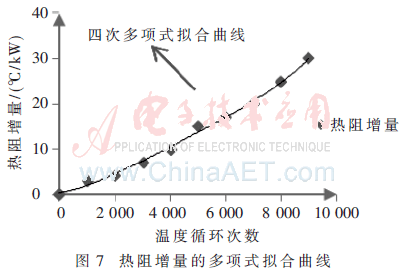
    R_thp=0.349 7+0.001 1x+7×10^-7x²-1×10^-10x³+6×10^-15x⁴

    式中：x为温度循环次数，R_thp为热阻退化量。

    对拟合模型进行方差分析，得到拟合系数R²=0.995 7，非常接近1，说明拟合程度很好，IGBT热阻在温度循环下的退化模型符合四次多项式模型。

4 结论

    随着温度冲击的不断增加，模块焊料层出现疲劳损伤，外部特征表现为器件热阻不断增大。对测得IGBT热阻的退化数据进行分析，发现退化数据符合多项式模型。在给定最佳模型判定条件下，对实验结果进行曲线拟合发现本次实验IGBT热阻退化规律最佳拟合模型为四次为多项式模型。

参考文献

[1] 王兆安，黄俊.电力电子技术[M].北京：机械工业出版社，2000.

[2] AMRO R，LUTZ J.Power cycling with high tcmpcrature swing of discrete components based on different technologies[C].IEEE PESC.Piscataway，USA：IEEE，2004：2593-2598.

[3] HAMIDI A，BECK N，THOMAS K，et al.Reliability and lifetime evaluation of different wire bonding technologies for high power IGBT modules[J].Microelectronics Reliability，1999，39：1153-1158.

[4] BERG H，WOLFGANG E.Advanced IGBT modules for railway traction applications: reliability testing[J].Microelectronic Reliability，1998，38：1319-1323.

[5] 杜熠，李璠，曾照洋，等.IGBT性能退化模型构建方法研究[J].电力电子技术，2013，47（1）：104-106.

[6] 杨旭.基于饱和压降测量的IGBT功率模块状态评估方法研究[D].重庆：重庆大学，2012.

[7] 陈明，胡安，刘宾礼.绝缘栅双极型晶体管失效机理与寿命预测模型[J].西安交通大学学报，2011，45(10)：65-71.