文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.02.007
中文引用格式： 孙晔，易克初，向新，等. 脉冲测距系统的多径干扰影响及消除[J].电子技术应用，2016，42(2)：28-31.
英文引用格式： Sun Ye，Yi Kechu，Xiang Xin，et al. The effect and elimination of multipath interference in pulse distance measuring system[J].Application of Electronic Technique，2016，42(2)：28-31.
0 引言
机载无线电导航系统是保障飞行安全的重要系统，也是飞机最为基本的航电系统，其精度的提升对飞行的重要性不言而喻。显然，选择一种合适的导航方式，并且选取满足精度要求的导航设备对于实现精确导航起着重要的作用。长期以来，利用TOA方法实施导航是导航定位系统中应用最为普遍的方法之一，基于该技术形成了脉冲测距系统，该系统主要用于测量飞机距导航台的斜距，其机载设备就是大家所熟知的DME(Distance Measure Equipment)，该设备可与其他导航设备如VOR(VHF Omni-directional)、ILS(Instrument Landing System)等协调工作，为飞机提供高精度的近进导航服务。由于DME设备与地面导航台之间通过询问-应答方式完成导航工作，其信号的传输受到地空无线信道的影响[1]，由于地空无线信道通常建模为多径信道（常见为双径信道），多径干扰会造成脉冲检测的误差，并继而造成测距精度的下降[3]。本文的目的在于针对这种情况，以DME设备为对象，确定多径现象对系统误差造成影响的原因，提出一种针对多径消除的基于第一脉冲延迟译码的解决方案，并完成脉冲译码电路的设计。
1 脉冲测距系统概述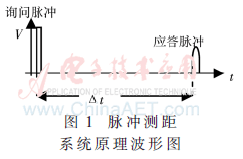
1.1 脉冲测距系统工作原理
DME采用询问-应答式测距原理，如图1所示。假设被测距离为R，C为光速，Δt为测量设备中询问脉冲到应答脉冲间的时间间隔，其中包含系统的处理时间和固定延迟，记作td，因此距离R满足公式：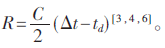
1.2 脉冲编译码的抗干扰作用
为了降低系统假截获概率，通常可采用脉冲编译码的方法来克服各类干扰，其中包括：重复频率、载频、脉冲数码及间隔和脉冲宽度编译码[3]。DME系统综合采用以上四种方式。抗干扰具体参数：脉冲宽度询问通道3.2 μs，应答通道3.5 μs；两个通道载频工作于L波段相差63 MHz；搜索状态重复频率150 Hz；采用双脉冲编译码。这些措施有效克服了噪声干扰、同型测距器的脉冲干扰、直达干扰、无源反射目标干扰等，大大地提高了正确截获的概率。经过脉冲编码后系统的波形图如图2所示。
由图2可以看出，经过脉冲数目和间隔编译码的测距系统，发射和接收的脉冲是一组间隔不同编码脉冲。译码电路根据编码标准对符合相应格式的询问和应答脉冲进行相关性解调[5]，从而达到识别“协定信号”格式，减小干扰的目的。而解算电路常采用译码得到的“最后”一个脉冲位置，作为计时的标准计算距离R，询问和应答脉冲间隔的不同所引入的时间差通常被计算在系统总延迟中。
2 脉冲测距系统的多径干扰
多径现象的产生主要是由于传输路径中的反射物对无线电波的反射造成。它的主要影响是在接收天线端产生许多辐射信号的“复制品”，这些“复制品”称为“多径成分”，表现为经过不同路径产生随机的延迟和衰减[1，2，6]。多径现象作为一种干扰对脉冲测距系统的测距准确性有很大的影响，上述脉冲编译码方案虽然可以大幅减少系统中的干扰脉冲数量，但是却很难克服多径干扰，这主要是因为多径干扰无论是载频、重复频率、脉冲宽度还是脉冲数目和间隔都与有效信号完全一致。
多径干扰对脉冲测距系统的影响主要为多径成分经随机延迟后在有效信号的脉冲波形上叠加，使波形产生畸变，从而影响测距的准确性。DME系统通常工作在LOS环境下，一般采用高斯波形或准高斯波形，其仿真波形如图3所示。图中幅值较大的波形为有效信号，幅值较小的波形为多径成分，根据其第二径延迟与直达路径的关系可以分为三种情况，即第二径小于脉冲间隔，与脉冲间隔相当以及大于脉冲间隔。
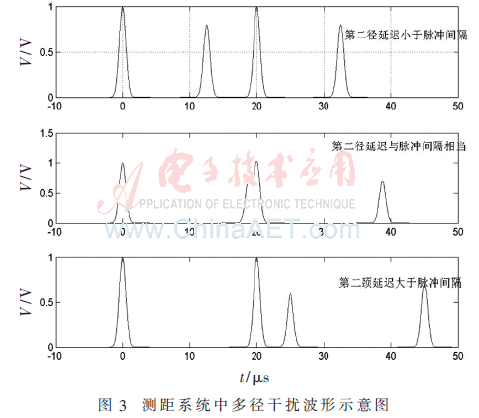
显然第二种情况由于存在脉冲混叠现象，导致前沿发生变化，测距的基准取样点前移，因而对于脉冲测距准确性的影响最为严重；其余两种情况的干扰基本可以采用传统的译码方案或文献[5]中的译码方案以及脉冲测距“截获”和“搜索”过程将其滤除。本文所讨论的多径干扰主要针对与脉冲间隔相当的情况。
3 延迟译码消除多径干扰原理分析
文献[5]中提到的译码方案和传统的译码方案被称为第二脉冲译码方案，这主要是因为译码输出的波形前沿，即距离测算电路的计时基准点通常取决于第二脉冲的前沿时刻，当系统受到多径分量的影响时，测距的准确性会大大降低。
在LOS传输环境中，多径延迟必然出现在有效信号的第一脉冲之后[3，4]，因此采用第一脉冲前沿作为距离测算电路计时的基准就可以消除多径干扰所引入的误差，提高测距的准确性，这就是基于第一脉冲延迟译码消除多径干扰原理。图4给出了DME系统X模式下，第一脉冲延迟译码的原理波形图。图中A为原始脉冲波形，B为整形后的方波，C和E为不同延迟的波形，D为B和C相与并展宽后的波形，F为D和E相与波形，即译码输出波形。显然，F脉冲相比B波形第一脉冲的延迟是固定的，不受多径的影响。
4 第一脉冲延迟译码的FPGA实现
4.1 基于FPGA的第一脉冲译码方案
译码电路是脉冲测距系统接收机的重要组成部分，在设计时应该遵循“译码电路能够检测并识别接收脉冲编码对所有信息”，具体可以总结为以下几点原则：
(1)能够识别系统规定的脉冲宽度，在规定技术指标要求下，自动滤除不符合要求的脉冲；
(2)根据系统规定的脉冲间隔，识别编码脉冲组中每一个脉冲的空间位置，滤除不符合规定间隔的脉冲对；
(3)译码电路输出单脉冲，其前沿作为计时基准；
(4)对于第一脉冲译码而言，还需注意译码输出脉冲前沿与第一脉冲前沿间隔是固定值。
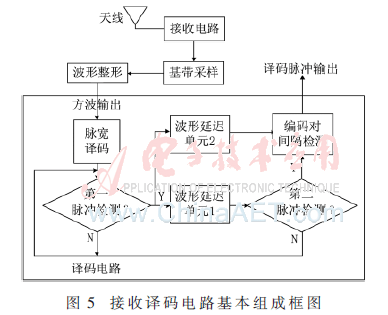
本方案基于设计灵活、调试方便的FPGA进行开发，根据上述原则设计的电路组成主要包括：波形整形、脉冲宽度译码、脉冲间隔译码和波形合成整形电路，其功能分别是将采样的脉冲波形整理成方波；滤除过宽和过窄的脉冲；脉冲编码相关检测和译码输出脉冲整形。其中脉冲间隔译码电路包括：第一脉冲检测、波形延迟和第二脉冲检测和编码对间隔译码四个单元，如图5所示。
4.2 FPGA实现
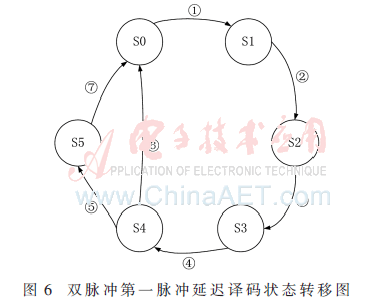
显然，上述方案中脉冲间隔译码电路是核心单元，设计中采用了状态机的设计思想，设置了S0~S5共6种状态，分别代表译码电路不同的工作状态，箭头代表状态跳转的方向，状态转移图如图6所示。其中S0：系统的初始状态；①无条件；S1：判断方波中“0”的持续时间；②根据DME系统实际情况，设置为当“0”持续40 μs即转换；S2：判断方波中“1”的持续时间，也即脉冲宽度的大小；③根据DME系统中脉冲宽度不小于3.2 μs，此处设置为脉宽大于1.6 μs即转换，小于1.6 μs的脉冲信号被视为干扰自动滤除；S3：判断第一脉冲到下一个脉冲的间隔时间；④根据DME系统不同的工作状态，可以灵活设置转换时间，但每个DME工作状态下该时间是固定的；S4：判断第二脉冲是否出现，宽度是否满足要求；⑤脉宽达到1.6 μs或以上时，转换到S5，同时输出译码后的波形；S5：判断波形的是否再次回“0”；⑥第二脉冲没有在系统规定的位置处出现，此时跳转回S0初始状态，重新判断；⑦当完成一次译码后，在第二脉冲的后沿，状态跳转回S0，准备下一次译码。
4.3 仿真结论
本文在QuartusII环境下使用Signaltap工具进行了设计方案抗多径延迟的仿真，针对DME系统X模式下（脉冲间隔为12 μs，-3 dB处脉冲宽度为3.5 μs），采样时钟100 MHz，采样深度为16 K，“同步数字方波信号digital_pulse”信号上升沿触发。
图7给出了第二径位于不同位置时，译码电路各节点输出的波形，其中①同步方波脉冲信号；②采用正交采样所得到的原始波形；③-6 dB取样进行波形整形后的方波；④经过脉冲宽度译码及第一脉冲检测电路输出波形；⑤延迟单元1对原始波形延迟了12 μs后的波形，用来进行第二脉冲位置检测；⑥延迟单元2对原始波形延迟13 μs的波形，用来进行编码对间隔检测；⑦经过编码对间隔检测后，译码电路输出的译码脉冲。表1给出了不同延迟情况下，多径对脉冲间隔的影响和该方案延迟译码后时间基准取样点的延迟。
由图7和表1，不难得出以下结论：
(1)观察图7中①-⑦信号的波形说明，该设计方案满足了第一脉冲译码方案的设计原则，对脉冲宽度、脉冲间隔和所有脉冲位置进行了准确的检测或识别，符合设计需求。
(2)对比观察表1第4行和第5行，在不同多径延迟影响条件下，图7中信号③和④脉冲间隔发生了变化，但是信号⑦脉冲的位置，其相比第一脉冲的延迟量恒为定值；
(3)基于第二条结论，选取译码电路输出脉冲前沿作为时间基准取样点，取样点不受多径的影响，能够克服多径的干扰，测距精度能够保证。
5 结论
由于采用第二脉冲译码的方式，所以多径延迟分量若接近第二脉冲的位置，则容易对脉冲测距系统准确性造成影响。据此本文采用第一脉冲延迟译码方案，该方案可有效地克服多径干扰对脉冲测距系统准确性的影响；论文中对该方案采用FPGA予以实现，仿真测试结果表明，基于第一脉冲延迟译码电路有效地消除了多径的干扰，提高了数字化脉冲测距系统的测距精度。
参考文献
[1] BELLO P A.Aeronautical channel characterization[J].IEEE Trans.Commun，1973，COM-21：548-563.
[2] Haas Erik.Aeronautical channel modeling[J].IEEE Transactions on Vehicular Technology，2002，51(2)：254-264.
[3] 王芳，秦伟.影响DME测距精度的因素分析[J].科技创新导报，2013(36)：56-57.
[4] 王鼎，张晓梅，栾宝宽.塔康地面信标半幅探测电路对测距精度的影响分析[J].现代导航，2014，2(5)：117-120.
[5] 孙晔，陈高平，郭岩.一种基于FPGA/CPLD的脉冲测距系统译码方案[J].弹箭与制导学，2006，26(3)：256-258.
[6] Li Kuangmin，Pelgrum Wouter.Optimal time-of-arrival estimation for enhanced DME[C].Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation.ION GNSS 2011，Portland，2011：3493-3502.