摘要：提高移动通信话务量的预测精度对提高网络性能、增进用户体验具有重要意义。由于多种因素会影响到移动通信话务量的准确预测，故选择多因素灰色话务量预测模型来预测话务量。先对数据进行预处理，用关联分析法找到影响话务量预测的主要因素。但此模型对波动较大的数据预测精度较低，用支持向量机的模型来改善预测结果，选取拥有较强的敛散性和全局寻优能力的复高斯小波核函数优化向量机。从仿真结果可以看出该模型有更好的收敛作用和较为理想的预测效果。

　　关键词：复高斯小波核函数；支持向量机；多因素；话务量预测

0引言

　　话务量预测，是指以历史话务量数据为基础，从一定的规律性与特点出发，通过统计调查，运用科学有效的建模方法对未来某一时段的话务量进行预测。通过对预测结果的分析，可以清楚地知道哪些网络需要扩容，哪些网络需要优化压缩。通常情况下预测话务量所采用的方法有线性自回归移动平均模型（ARIMA）［1］、人工神经网络（ANN）［2］、支持向量机（SVM）［3］等。其中线性自回归移动平均模型［4］要求训练数据的时间序列应具有正态分布、全局平稳等特征，但在实际应用中，话务量的时间序列往往是不规则、非平稳且非线性的。人工神经网络［5］相比线性自回归移动平均模型有较好的非线性预测能力，但要求训练样本数据量较大，且易于陷入局部极值，会导致最终的预测效果不稳定。普通的预测模型大多数是根据过去的话务量去预测未来的话务量，但并没有将相关因素考虑在内，如果没有考虑影响因子，预测结果就会有一定的失真。为了能够准确地预测未来话务量的变化趋势，本文从多因素的角度，提出了一种改进的复高斯小波核函数优化支持向量机的多因素灰色预测模型［6］。根据收集到的话务量数据和影响因素，用灰色关联分析法计算出对话务量影响较大的因素有系统接通率、忙时用户数、开机用户数、小区切换次数。使用MATLAB进行仿真，将预测结果与粒子群优化支持向量机的多因素灰色模型、多因素灰色模型、真实值比较，本文算法的预测结果与真实值更接近。

1本文改进的多因素灰色模型相关原理及算法

　　1.1数据的选择及预处理

　　分析往年的话务量数据可以发现，话务量会随着时间和季节的改变而明显发生变化，比如白天的话务量比夜晚高，节假日的话务量明显高于平时。假如将话务量看做一个时间序列，那它具有季节性和周期性。

　　由于收集到的话务量数据有限，本文将侧重于传统节假日忙时话务量的预测。收集了安庆移动2011年~2015年每年五一之前20天的话务量数据以及影响因素的资料。在此基础上，对其在五一的忙时数据进行仿真实验，预测忙时话务量数据。首先将实际数据进行归一化，将归一化后的数据通过灰色关联分析后得出结果数据，再用提出的改进模型进行预测。

　　1.2灰色关联分析

　　由于话务量受多种因素的影响，本文采用灰色关联分析法［7］来判断话务量与多种影响因素间的相关度大小，选择与话务量相关性较大的因素。

　　灰色关联分析的主要原理是根据序列曲线几何形状的相似程度来判别其联系是否紧密。通过计算数据间相关度的大小来判别话务量与各因素相关性的大小。

　　（1）设系统特征序列X1，相关因素序列Xk：

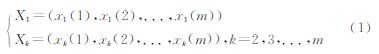
　　（2）对各数据序列进行处理：

　　Yk=Xk/xk(1)=(yk(1),yk(2),...yk(m))

　　k=1,2,...,m（2）

　　（3）计算相关系数：

　　（4）根据各数据序列关联系数的大小，计算关联度的值：

　　对话务量影响较大的因素与话务量间的关联度结果如表1所示。

　　1.3多因素灰色模型

　　多因素灰色模型MGM(1，n)［8］是利用n元一阶常微分方程组来描述n元相关联变量的状态，并进行未知状态预测。核心思想是先进行数据预处理，使得新生成的数列具有单调性，再对新生成的序列构建n个一元微分方程组，优化目标函数，找到相对误差最小的模型参数，最终可以实现预测未来的话务量。算法步骤如下：

　　假设某个系统经过灰色关联分析后有n个影响因子,每个影响因子有m个数据:

　　（1）输入原始序列，进行累加：

　　x1={x1i(j)}（5）

　　其中{x1i(j)}=∑kj=1x0i(j)，i=1,2,...,n，j=1,2,...,m

　　（2）多变量灰色模型MGM(1,n)对累加后的数据建立n元一阶微分方程组，简写为：

　　其中X(1)=(x(1)1(j),x(1)2(j),...,x(1)n(j))

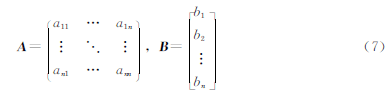
　　令D=(A,B)T=［ai1ai2…ainbi］T，i=(1,2,…,n),若LTL可逆，则可得D的辨识值：

　　D′=(A′,B′)T=(LTL)－1LTY，i=1,2,...,n（8）

　　计算模型参数的估计值，由式（8）得到A、B的辨识值A′、B′：

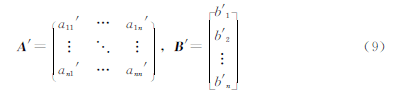
　　（3）计算模型的拟合值或预测值。由式（6）可得到预测值：

　　x′(1)i(j)=eλ(j－1)(x(1)i(1)+A′－1B)－A′－1B′（10）

　　最终的预测值为：

　　x′(0)i(1)=x′(1)i(1)

　　x′(0)i(j)=x′(1)i(j)－x′(1)i(j－1)， j=2,3,…（11）

　　通过以上多因素灰色模型的计算公式，可计算出时间序列的模拟值。但对于波动较大的时间序列，计算出的模拟值误差较大。把安庆移动2011年~2015年每年“五一”之前20天的话务量数据及表1中相关因素的数据作为MGM(1,4)模型的输入变量进行预测，可得到2015年“五一”话务量的预测趋势，预测结果如图1。

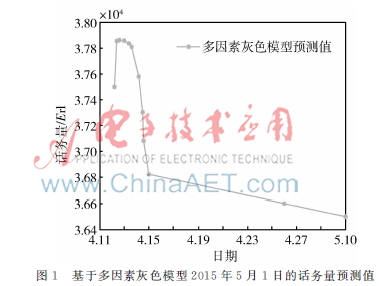
　　图1基于多因素灰色模型2015年5月1日的话务量预测值

　　1.4基于复高斯小波核函数优化的向量机

　　支持向量机预测模型［9］的预测精度，主要受到两个参数的影响：惩罚因子和核函数。由于复高斯小波核函数［10］拥有较强的敛散性和全局寻优能力，为了进一步提高预测精度，提出了基于复高斯小波核函数的支持向量机预测模型对残差序列进行预测［11］。残差序列是由原始的真实序列与上一步多变量灰色模型得到的模拟值对应相减得到。

　　设有样本集{(xi,yi),i=1,2,...,n}，其中xi∈Rd为输入样本，yi为输出，不敏感损失函数ε的定义是：

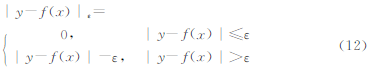
　　回归函数的表达式为：

　　f(x)=［ω·φ(x)］+b（13）

　　其中φ(x)是从低维到高维的映射函数，ω表示权值参数，b表示偏差参数。

　　回归函数的优化目标函数为：

　　minω,b,ξ12ω2 +C∑ni = 1(ξi  + ξ*i )（14）

　　目标函数的约束条件为：

　　st|yi -(ω·φ(x))-b|≤ε + ξ*i

　　其中，ξi ≥0,ξ*i ≥0,i = 1,2,...,n。

　　构造拉格朗日函数，将带约束条件的目标函数转变为无条件下的目标规划问题。

　　L(ω,b,ξ,ξ*)=12ω2+C∑ni=1(ξi+ξ*i)-

　　∑ni=1αi［ε+ξi-(yi-(ω·φ(x))-b)］-

　　∑ni=1α*i［ε+ξ*i-(yi-(ω·φ(x))-b)］-

　　∑ni=1(βiξi+βiξ*i)′（15）

　　对上式中的参数分别求导，并令偏导为零：

　　maxα,α*,β,β*-12∑ni=1∑nj=1［(αi-α*i)(αj-α*j)K(xi-xj)］-

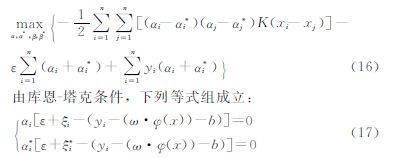
　　上式中，α,α*中至少有一个为零，α≠0对应的样本点xi被定义为支持向量，根据支持向量进行求解，便可得到支持向量机的预测函数表达式：

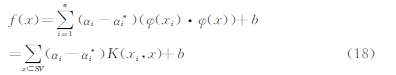
　　K(xi, x)为支持向量机预测函数表达式中的核函数, 采用的是复高斯小波核函数［12］。

　　使用安庆移动2011~2014四年的“五一”前20天的数据以及2015年“五一”数据的残差序列作为已知数据来训练预测模型，仿真结果如图2所示。

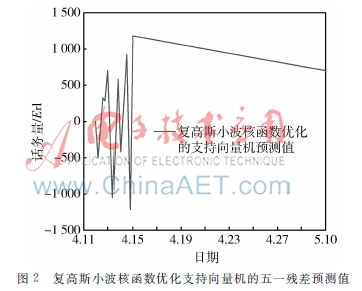
　　1.5本文算法主要思想

　　（1）用灰色关联分析法计算出特征序列与各相关因素序列之间相关度的大小，根据相关度的大小，找出影响话务量较大的因素。

　　（2）将对话务量影响较大的因素作为MGM(1,n)模型的输入，实现对话务量基本规律的预测，并得到预测的残差序列。

　　（3）利用复高斯小波核函数优化的支持向量机模型建立残差序列预测模型，从而实现对残差序列的预测。

　　（4）将MGM(1,n)的预测结果与残差序列预测结果叠加，实现对话务量的预测。

2仿真实验结果分析

　　为了验证本文所提算法的预测结果，选取了粒子群［13］优化的支持向量机的多因素灰色模型、多因素灰色模型作为比较模型。其中粒子群算法的基本参数为：粒子群种群规模m=100，最大迭代次数为1 000，学习因子c1=c2=2,惯性权重ω=09，松弛因子ε=054，粒子的初始化速度为0，最小适应值ξ=001,通过粒子群优化算法确定C=0616 0，g=10983 6。对2015年“五一”的忙时话务量进行预测，仿真结果如图3所示。　　

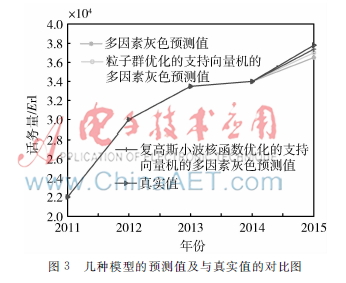
　　通过对话务量的仿真分析，证明了该模型相较传统的多因素灰色模型预测精度高，对波动较大的数据预测比较准确。采用相对误差的方法对预测结果进行分析，计算结果如表2所示。

3结论

　　本文选择预测精度较高的预测模型对话务量进行预测，话务量的预测精度越高，对移动网络通信的指导意义就越大，越能及时应对网络可能出现的拥塞情况。在研究了国内外预测领域的最新进展后，针对话务量的预测，本文提出了基于复高斯小波核函数改进支持向量机的多因素灰色预测模型。在进行预测之前，搜集了大量话务量的历史数据和相关因素数据，对2015年“五一”的忙时话务量进行了预测。

　　由于话务量受多种因素的影响，选择多因素灰色话务量预测模型。此模型适合由多种因素影响的话务量的预测，而且算法比较简单。但是当数据波动较大时，多因素灰色预测模型预测精确度较低，针对这种情况，本文提出用支持向量机的模型来修正灰色模型的预测结果。

　　核函数与支持向量机的预测精度相关，通过改进核函数，可提高预测精度。复高斯小波核函数拥有较强的敛散性和全局寻优的能力，通过实验仿真，得出改进的模型相比多因素灰色模型、粒子群优化支持向量机补偿的多因素灰色模型有更好的收敛效果和较为理想的预测结果。

参考文献

　　［1］ 彭宇,雷苗，郭嘉，等.基于先验知识的移动通信话务量预测［J］.电子学报，2011,39(1):190-194.

　　［2］ 张一农,刘伯龙，王文婷.基于神经网络的客服中心话务量预测模型［J］.吉林大学学报（信息科学版）,2011,29(2):97-101.

　　［3］ Chen Dianbo, Xu Fucang, Wu Min. Traffic based on clustering and support vector machine forcasting model ［J］. Journal of Control Engineering, 2009, 16(2):195-198.

　　［4］ 张伟, 张新波. 移动GSM网话务量的ARIMA模型的建立及其预测［J］.数学理论与应用，2008(2)：70-74.

　　［5］ 吴永明,吴晟. 改进的遗传算法在神经网络结构优化中的应用［J］. 微型机与应用,2011,30（3）:79-81，85.

　　［6］ Pai Pingfeng，LIN C. A hybrid ARIMA and support vector machines model in stock price forecasting［J］.Omega，2005，33(6)：497-505.

　　［7］ 李鹏,刘思峰.基于灰色关联分析和D—S证据理论的区间直觉模糊决策方法［J］.自动化学报, 2011, 37(8): 993-998.

　　［8］ LUO Y. Nonequidistant MGM(1,n) based on vector continued factions theory and its application［J］. Information Technology Journal, 2014,13(6) ,1186-1191.

　　［9］ 陈电波,徐福仓,吴敏． 基于聚类和支持向量机向量机的话务量预测模型［J］. 控制工程, 2009, 16( 2) : 195-199.

　　［10］ 陈中杰,蔡勇，蒋刚.基于复高斯小波核函数的支持向量机的研究［J］.计算机应用研究,2012, 29(9):3263-3265.

　　［11］ 侯伟真,潘美芹. 高斯核支持向量机最优模型参数选择搜索算法［C］. 中国运筹学会第八届学术交流会论文集. 2006：716-722.

　　［12］ 林继鹏, 刘君华. 基于小波的支持向量机算法研究［J］. 西安交通大学学报， 2005，39(8)：816-819.

　　［13］ WANG F S, CHEN L H. Particle swarm optimization(PSO)［J］. Encyclopedia of Systems Biology, 2013,12(8):1649-1650.