基于PID控制LLC微波电源的仿真研究-AET-电子技术应用

基于PID控制LLC微波电源的仿真研究

2016年微型机与应用第1期

钱素琴，黄新明

（东华大学信息科学与技术学院，上海 201620）

摘要： 研制了一款基于PID控制输出电压的高频软开关电源。主电路采用了倍压整流输出LLC谐振变换器，利用PID控制闭环电压反馈，并通过对谐振变换器的特性分析绘制了直流增益曲线。根据理论分析与计算并结合实际调试情况，对LLC微波电源的主要参数进行设计，得到的仿真实验结果验证了分析计算的正确性。

关键词： LLC谐振变换器 PID控制零电压开关微波炉磁控管

Abstract：

Key words :

　　摘要：研制了一款基于PID控制输出电压的高频软开关电源。主电路采用了倍压整流输出LLC谐振变换器，利用PID控制闭环电压反馈，并通过对谐振变换器的特性分析绘制了直流增益曲线。根据理论分析与计算并结合实际调试情况，对LLC微波电源的主要参数进行设计，得到的仿真实验结果验证了分析计算的正确性。

　　关键词： LLC谐振变换器；PID控制；零电压开关；微波炉磁控管

0引言

　　随着家用微波炉的普及使用，传统微波炉磁控管的供电电源效率低、功率不可调、噪声大等缺点日益明显。如果微波电源能实现功率连续可调、零电压开关、PID控制等特性，将可有效地克服上述缺点。在对变换器拓扑结构考虑上，LLC谐振变换器相对其他拓扑，具备了工作范围广、调节效率高、通态损耗低等特点。国内一些学者对这一拓扑结构的参数最优化、提高功率密度等方面进行了研究，并取得了一定成果［13］，但研究偏向于低频低压情况。国外的学者对这一拓扑结构研究较早，但主要是对变换器高频率时的低效率问题进行研究［47］,对高功率高频段应用研究较少。文献［811］对高压多谐振直流输出进行了介绍。本文在充分研究了LLC谐振及微波电源磁控管的基础上，进一步分析提出了一种利用PID控制电压输出，采用倍压整流作为磁控管输出端电路的模型，并设计了主电路的参数，结合实验仿真进行了论证。此方面的研究对提高微波炉烹饪效率、提高微波炉的智能化程度、响应国家发展低碳经济等具有重要的意义。

1主电路结构

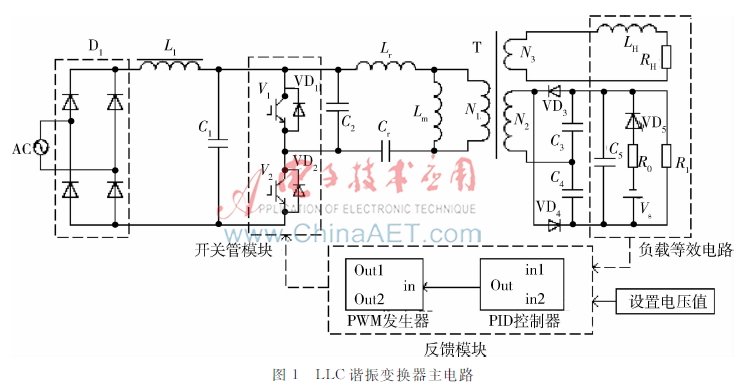
　　所采用的变频微波炉电源LLC谐振变换器的主电路模型如图1所示。其中，L1为滤波电感，C1为滤波电容，L1、C1与D1模块组成整流滤波电路。开关管模块由两个带有反并联二极管的开关管组成。Lr、Lm和Cr分别为谐振电感和谐振电容。T为理想变压器。负载等效模块用于等效负载阴极与阳极间的寄生电容，R1和R0分别为谐振状态和非谐振状态的负载等效电阻。反馈模块由PID控制器和PWM脉冲发生器组成，其中PID控制器可对负载电压进行反馈，PWM脉冲发生器可产生两路占空比互补、频率可调的脉冲，可为开关管模块提供输入脉冲。变压器副边采用了倍压整流电路，以便在磁控管的阳极和阴极之间输出稳定的直流电（Uout≈4 000 V）。负载端的VD3、VD4、C3和C4共同组成倍压整流电路。C1为滤波电容，使用小容量无极性电容。

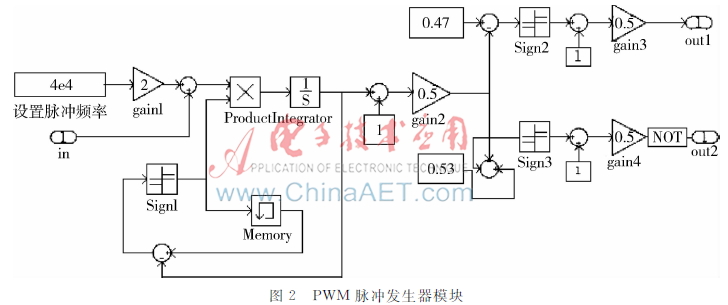
　　图2所示为PWM脉冲发生器内部实现模块。图中in为该模块的输入端，其值取自PID控制器通过对输出电压偏差值的调节得到的反馈值。该模块通过输入端in与设定的基础脉冲频率叠加，实现实时自动调节产生脉冲频率的功能，并通过积分器及符号函数模块产生三角波，而后通过比较器生成占空比互补的两路脉冲。　　

　　如图3所示，使用交流分析法等效出LLC谐振变换器的电路结构，并根据由此等效得到的电路来进行输入特性分析计算。

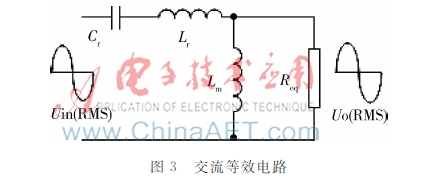
　　根据图3的等效电路，假设输入直流电压为Uin，输出直流电压为Uo，负载电阻为R。通过理论计算可得到：Uin(RMS)（谐振电路输入电压的基波有效值）、Uo(RMS)（谐振电路输出电压的基波有效值）、Req（副边实际负载电阻折算到原边的电阻值），由此可求得交流基波电压增益。

　　假设f为主电路开关管模块输入脉冲的频率，k=Lm/Lr，便可以求出fs（串联谐振的频率）、Q（串联谐振网络的品质因数）和ω，公式如下：

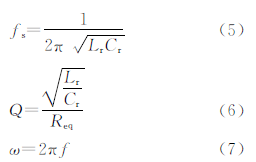
　　将以上参数代入式（4）中得：

　　则直流电压增益为：

3LLC谐振变换器直流增益曲线分析

　　为了分析不同参数值对直流电压增益的影响，使用MATLAB工具进行增益曲线的绘制。由于匝比n、Q值及k值对直流增益曲线的变化均有影响，故利用控制变量法对逐个因素进行分析。

　　首先对k值进行分析。将匝比n和Q值取固定值，取不同的k值进行绘制相应情况下的增益曲线。如图4所示。取不同的k值，得到的曲线各不相同，因此确定k值对直流增益有影响。图4中，横坐标代表归一化频率，当其在增大的过程中，每条曲线都是先增大后减小。给定的k值越大，所能获得的最大直流增益越小，且到达最大直流增益时对应的频率也越小。因此当k值偏大，而输入电压的值较小时，由于最大直流增益过小，很可能导致无法输出所需幅值的电压。从增加直流增益的角度来分析，应尽量使k值减小，使获得的最大增益增加。但从变换器的损耗来看，由于k的取值与Lm成正比，因此当k选取较小值时，会导致谐振网络的励磁电感变小，在相同输入的情况下，励磁电流会增加，导致谐振网络的损耗增加。综上分析可得，k值应在损耗和直流增益二者之间取折中值为宜。图4不同k值的谐振网络直流增益曲线

　　图5中绘制的是LLC谐振变换器中当匝比n和k值一定时，不同Q值所对应的直流增益曲线。从图中不难发现，Q值不同时，每条增益曲线各不相同，因此可知Q值对直流增益有影响。在归一化频率增大的过程中，每条曲线都是先快速增大而后慢慢减小。Q值越大，所能到达的最大直流增益越小，且到达最大直流增益时的归一化频率越大（越接近于1），即越接近于谐振频率。图中的5条曲线均通过了相同的一点，即谐振发生时，此时的归一化频率等于1，所有的Q值下的直流增益均相同。此时的直流增益只与n有关。当选取了适合的匝比n时，能使变换器始终工作于合适的频段内。如果选取了过小的匝比n，则f有可能大于fs，这样就无法始终满足零电压导通的条件。如果选取了过大的匝比n，则f有可能小于fs，导致变换器的实际频率距离谐振频率过远。从图中可以看出，当归一化频率位于02~1之间时，直流增益的变化幅度随k值的减小而增大。由于需要使用PWM脉冲发生器产生不同的频率来改变输出的电压值，因此在选取工作频段时应挑选电压增益较敏感的频段，因此f不宜大于fs，即归一化频率不宜大于1，否则容易造成调节灵敏度下降。综上所述，在分析设计电源的工作频段时，应将频率f的变化范围固定在fr（第一揩振频率，fr=20 kHz）与fs之间。

4仿真和实验验证

　　4.1参数及仿真波形

　　通过上述的计算分析，研制了一台采用LLC谐振变换器与PID控制反馈相结合的变频微波电源样机，经过多次的仿真参数调整后，将电路中主要的元件参数选定为：L1=120 μH, C1=5 μF, C2=02 μF, Lr=16 μH, Lm=45 μH, Cr=38 μF，变压器匝数比n为1∶19,C3=5 600 pF ,C4=5 600 pF。如图6所示，开关管能够实现零电压导通，谐振电容上的电压波形近似正弦波，证实了对LLC谐振变换器特性的计算和分析的正确性。

　　4.2仿真实验结果

　　使用PWM脉冲发生器模块电路作为LLC谐振变换器的控制器，将脉冲发射频率控制在最高40 kHz、最低20 kHz之间。如图7所示为输出电压的实验波形。容易发现，输出电压经PID控制反馈调节后其波形可看作一条近似直流电压与一个100 Hz的梯形波叠加而成，输出值可以在短时间内（约006 s）达到稳定状态，稳定的输出电压接近4 000 V，与预期计算的电压值吻合，可以为磁控管负载供电。

　　当微波电源带磁控管负载时，输出功率很难测定。为了得到电源效率与输入功率之间的关系，使用大功率的电阻来模拟负载，通过改变PWM脉冲发生器产生的频率来反馈得到相对应的电压值，输入功率Pin在很宽的范围（600～1 200 W）内时，电源效率能达到88%以上，证实了采用PWM脉冲控制PID调节的设计及谐振网络的零电压开关设计可以大幅度地降低开关频繁通断损耗，从而提高电源的使用效率。

5结论

　　通过实验得出以下结论：

　　(1)在LLC谐振变换器中负载端使用零电压开关来降低损耗的设计是有效的，利用LLC谐振变换器特性得出的直流增益曲线是正确的，对微波电源的参数设计是合理的。

　　(2) 在LLC谐振变换器的主电路中加入PID控制可以有效缩短电压达到稳定值的时间，修改开关管输入脉冲的频率可以达到快速稳定地调节电压的目的。

　　(3) 开关管频率在20～40 kHz的开关频率范围内，可实现磁控管的输出功率线性连续可调，通过仿真实验不断设定和改变频率的取值，验证了零电压开关特性在所属频率范围内都是安全有效的。

　　(4) 研究倍压整流式LLC谐振变换器拓扑的设计思路和方法可以类推到其他的高频微波电源领域。

参考文献

　　［1］王春芳，张志勇，朱世盘. 基于LLC谐振变换器的微波炉用高压变频电源［J］. 电工电能新技术，2013，32(3):101-104.

　　［2］陈伟，王自强. 半桥LLC谐振变换器稳态建模及分析［J］. 通信电源技术，2008，25(4):17-19.

　　［3］赵晨，石洋，吴新科，等. 三元件串联LLC谐振变流器的优化设计策略［J］. 电工技术学报，2008，23(1):65-71.

　　［4］王兆安，刘进军. 电力电子技术［M］. 北京：机械工业出版社，2009.

　　［5］杨铭，倪喜军，白杰，等. 新型微波炉电源中ZVS高频变换器的设计及实现［J］. 电源技术应用，2009(3):30-35.