段廷银, 赵东明

郑州大学 信息工程学院， 河南 郑州 450001

　　摘要：协同过滤技术基于用户的评分历史预测用户对某一项目的评分。基于用户的协同过滤技术可以利用传统的欧氏距离发现与用户的兴趣相近的近邻。针对欧氏距离并不能很好地反应用户之间的近邻关系的问题，一种新颖的基于欧氏距离的最小最大距离的方法被提出，用来发现用户近邻，称之为流形近邻。实验结果表明，基于流形近邻的协同过滤框架（Collaborative Filtering based on Manifold Neighbors, MNCF）与目前的协同过滤算法相比，性能有一定的提高。

　　关键词： 流形近邻；距离空间；协同过滤；视觉距离；最小最大距离；推荐系统

0引言

　　协同过滤是Web 3.0时代一个新颖的技术，被广泛应用于各类电子商务网站。通常协同过滤算法分为两大类：基于内存的协同过滤算法和基于模型的协同过滤算法［1］。基于内存的算法［2］首先找到k个近邻，然后根据近邻进行推荐。基于模型的算法［35］通过学习用户的历史兴趣建立用户的偏好模型。基于内存的算法又可分为基于用户和基于项目的两大类。当前对协同过滤算法的研究主要针对数据稀疏性［67］和用户兴趣随时间漂移问题［89］等进行。随着云计算的发展，一些基于云计算的分布式协同过滤算法也被提出［1012］。

　　在实际应用中，传统的基于用户的协同过滤技术存在两个问题：第一，大量项目评分的缺失；第二，利用欧氏距离可发现与用户的兴趣相近的近邻，但是欧氏距离并不能很好地反应用户之间的近邻关系。对于第一个问题，一般设置缺失值为0。然而，用户对某一项目进行评分时心理有一个标准，根据大数定理，平均分最能代表该标准。因此，采用平均值替换缺失值更合适。本文提出了一种新颖的基于最小最大距离的方法来发现用户近邻，称其为流形近邻。然后基于KNN的思想，利用近邻对某一项目评分的加权平均值来预测用户对某一项目的评分。对于利用近邻不能预测的项目评分，使用用户对其他项目的均值作为对该项目评分的预测。基于以上方法本文建立一个基于用户的协同过滤框架，称之为基于流形近邻的协同过滤算法（MNCF）。

1相关工作

　　1.1符号约定

　　本文约定：

　　ri表示某一用户对项目i的评分；

　　i表示某一用户对项目i评分的预测；

　　wi表示用户i对用户a评分预测时的权重；

　　dmin_max(i,a)表示用户i和用户a的最小最大距离。

　　1.2最小最大距离

　　用户i和j之间的最小最大距离定义为：

　　dmin_max(i,j)=minkdkpij=minpkijmax(xp,xp+1)pkijdp,p+1（1）

　　其中,pkij是用户i和用户j之间的第k条路径，dp,p+1是路径上相邻节点之间的欧氏距离。当两个用户在同一个流形上时，其最小最大距离较小［13］。因此，它更好地反应了用户之间的近邻关系。

　　求解最小最大距离时，如果采用深度优先搜索或者广度优先搜索，时间复杂度是指数级的。当用户比较多时，直接求解最小最大距离变得不可行。然而，最小生成树（MST）恰是最小最大生成树［14］。求解最小生成树的时间复杂度为O(n2)。在最小生成树上，最小最大距离由式（2）计算。

　　ρ(i,j)=dmin_max(i,j)=max(xp,xp+1)pijdp,p+1（2）

2流形近邻协同过滤

　　2.1最小最大距离空间

　　距离空间是一种拓扑空间，其上的拓扑由指定的一个距离决定。

　　引理1最小最大距离可以确定一个距离空间。

　　证明:

　　(1)由式（2）得:

　　ρ(i,j)=dmin_max(i,j)=max(xp,xp+1)pijdp,p+1≥max(xp,xp+1)pij0=0

　　当且仅当i=j时，ρ(i,j)=0。

　　（2) 由于最小生成树是一个无向图，所以有：

　　ρ(i,j)=ρ(j,i)

　　（3）对任意i，k和j，如果k∈Pij，则：

　　ρ(i,j)=dmin_max(i,j)

　　=max(max(xp,xp+1)pikdp,p+1,max(xp,xp+1)pkjdp,p+1)

　　≤max(xp,xp+1)pikdp,p+1+max(xp,xp+1)pkjdp,p+1

　　=ρ(i,k)+ρ(k,j)

　　如果k∈Pi,*或者k∈Pj,*,与k∈Pi,j情形类似。否则，因为最小生成树连通，Pij上必然存在一点k′使得k′∈Pik并且k′∈Pkj。

　　ρ(i,j)≤ρ(i,k′)+ρ(k′,j)≤ρ(i,k)+ρ(k,j)

　　证毕。

　　2.2流形K近邻

　　定义与用户a流形距离最近的k个用户为用户a的k个近邻。

　　2.3视觉距离

　　基于人的视觉感知，敏感度大致上与输入信号的强度成对数关系，在考虑加权方案时，本文引入对用户间的最小最大距离进行对数变换的加权方案01VD。

　　2.4MNCF

　　流形近邻协同过滤框架MNCF算法描述如下：

　　输入：用户的评分记录。

　　输出: 用户对项目评分的预测。

　　（1)计算每个用户已经评论过项目的评分均值。

　　（2）把（1）中计算得到的平均分作为该用户对未评分项目的评分。

　　（3）计算每个用户之间的欧氏距离。

　　（4）以用户为点集，以（3）中得到的用户之间的欧氏距离为边的权值构造一个无向有权图。

　　（5）构造出（4）中无向有权图的最小生成树。

　　（6）利用（5）中的最小生成树根据式（2）计算用户间的最小最大距离。

　　（7）根据（6）中得到的最小最大距离求出每个用户的k个邻居。

　　（8）利用k个流形近邻对某一项目的评分的加权平均值作为用户α对未评分项目的评分。

3实验

　　选取Movie Lens数据集对本文提到的方法进行试验。Movie Lens 数据集包含100 000个评分（1~5分），它们是由943个用户对1 682个电影给出的评分。把数据集分割为两个不相交的子集，也即是80%的训练集和20%的测试集。

　　为了评估MNCF，本文采用了平均绝对值误差（MAE）［15］。

　　MAE的值越小，说明准确率越高。

　　3.1不同加权方案对MNCF的影响

　　用户i对用户a评分权重为wi时对应的加权方案如表1所示。不同加权方案对MNCF的影响如图1。

　　从图1中可以看出,当流形近邻数目较少时，加权方案EXND、01VD、01ED和SMN的结果相近。然而，随着流形近邻数目的增加，MAE的性能开始变差但趋于稳定。而01VD、01ED、SMN的性能在流形近邻数目足够大时才开始发生显著差异，并且01ED的性能表现最好。

　　3.2不同协同过滤框架的比较

　　在加权方案都取01VD的情况下，首先将MNCF与只使用用户已给出评分的平均值进行预测的算法（MCF）进行对比；然后与采用最小最大距离加上一定权重的欧氏距离的算法（EMNCF）进行对比。实验结果如表2所示。 

　　其中，EMNCF和MNCF的流形邻居数取500，EMNCF是在最小最大距离上加上0.01倍的欧氏距离。从表2中可以看出MNCF明显优于MCF，与EMNCF性能相当。

　　为了比较基于欧氏距离的协同过滤算法和基于最小最大距离的协同过滤算法，此处变化邻居数，加权方案取01VD，记使用欧氏距离的协同过滤方案为ECF，得到的实验结果如图2所示。　

　　从图2可以看出，使用流形近邻的协同过滤算法优于使用欧氏距离的协同过滤算法。

　　3.3不同流形邻居数对实验结果的影响

　　图3不同邻居数对预测性能的影响对于MNCF，让邻居数从100变化到900，加权方案取01VD得到的结果如图3所示。

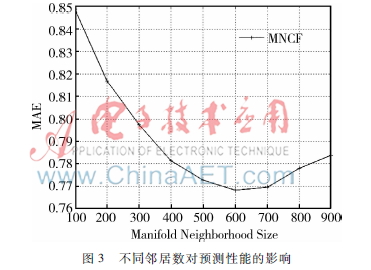
　　从图3中可以看出，当流形近邻数在训练集用户总数一半附近时，预测效果较好。

　　3.4与最新基于用户的协同过滤算法对比

　　从图4中可以看出，当流形近邻数在训练集用户总数一半附近时，预测结果的MAE控制在［0.77,0.78］之间（加权方案取01VD，流形近邻数目从400到600，依次增1）。与文献［8］、文献［16］(［0.80,0.82］)中的协同过滤算法相比，有一定提高。

4结束语

　　本文介绍了最小最大距离在电影评分预测中的应用。实验结果表明,本文提出的基于流形近邻的协同过滤算法与目前的协同过滤算法相比性能有一定程度的提高。在Movie lens数据集上为达到最佳性能，MNCF所需的流形邻居数目较多，主要原因应该是本文中的最小最大距离还是基于欧氏距离的。从实验结果可以看出，使用最小最大距离优于欧氏距离。本文的方法还可以被应用到社区发现、传感器网络、图像分割等领域。

　　在实际应用中，往往会有数以千万计的用户，在传统的单机系统上快速求解出最小最大距离显得不可行。然而，随着大数据时代的到来，基于MapReduce的Hadoop与Spark，旨在分布式处理实时数据的Storm，以及分布式大规模图像处理系统Pregel等大数据平台也得以飞速发展。接下来的工作是针对本文中的算法在Pregel和Spark GraphX等大数据平台上进行集群算法的研究与实现。

　　参考文献

　　［1］ BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering［C］.Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann Publishers Inc., 1998: 4352.

　　［2］ RESNICK P, IACOVOU N, Suchak M,et al. Grouplens: an open architecture for collaborative filtering of netnews［C］.Proc. of the ACM Conf. on Computer Supported Cooperative Work, 1994: 175186.

　　［3］ HOFMANN T. Probabilistic latent semantic analysis［C］.Proc of the 15th Conf. on Uncertainty in Artificial Intelligence, 1999:289296.