谢 俊，余水宝，田 聪

（浙江师范大学 数理与信息工程学院，浙江 金华 321004）

　　 摘  要： 无源滤波器在电力系统的谐波抑制方面应用广泛。对于电力系统中的谐波问题，提出了一种新颖的基于猫映射的混沌遗传算法（CGA）的无源滤波器的优化设计方法。通过对初始种群、交叉概率、海明距离等参数的改进并结合实数编码，提高了优化的效率和精度。最后，通过建立仿真实验对比研究，充分验证了该无源滤波器设计方法的有效性，并具有较好的谐波抑制效果。

　　关键词： 猫映射；混沌遗传算法；无源滤波器；优化

0 引言

　　电力电子器件和非线性负载在电网中大量应用，它们所产生的谐波可使电能质量产生很大问题并导致经济损失。同时各种敏感负载对电能质量的要求越来越高。无源电力滤波器因其电路结构简单、成本费用低、运行可靠性高等优点，是电力系统中应用最广泛的谐波抑制设备[1]。

　　关于滤波器的设计，目前国内外均未有标准的统一计算公式或设计程序。传统的无源滤波器参数设计方法普遍基于非线性规划且只针对单一设计指标，如电容器安装容量最小法、无功补偿容量法等，其LC参数的求取是通过计算和比较近似求解，因此无法实现全面优化。基于目前无源滤波器仅仅依据工程经验或简单技术经济指标来设计，以及现有的优化设计方法中某些方面存在的不足，本文提出了一种无源滤波器的多目标优化设计方法[2]，将无源滤波器的投资成本、无功补偿容量、滤波效果作为目标，利用基于猫映射的混沌遗传算法对无源滤波器的参数进行多目标优化设计。

1 猫映射的混沌遗传算法

　　1.1 猫映射的优越性

　　目前在混沌遗传算法中引入的混沌序列大多数采用Logistic混沌映射随机序列，其均匀性较差，生成的序列分布在边界点较多，在内部分散。这种分布特性会严重影响算法的收敛效率和收敛精度的提高。为了克服Logistic映射效率较低的问题，某些学者用Tent映射取代Logistic映射，虽然某些方面得到了改善，但是又引入新的问题，如运行时系统容易陷入小循环或不动点，最优解处在边缘时，出现无法获取最优解的问题[3]。针对遗传算法出现的较多问题，某学者巧妙地将遍历均匀性好、不容易陷入小循环或不动点的猫映射引入到混沌遗传算法中并进行一定的改进，提出了更为稳定有效、性能优异的基于猫映射的混沌遗传算法[4]。

　　1.2 猫映射的混沌分布

　　二维猫映射方程为：

　　式（1）表示为矩阵形式：

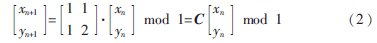
　　式（2）中，x mod 1=x-[x]，C=1 11 2。它的两个Lyapunov参数值为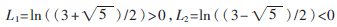。通过分析方程，可以得出猫映射具有混沌的特性。

　　根据参考文献[4]的分析，相同迭代次数情况下，与Logistic映射、Tent映射进行比较，猫映射的取值曲线分布得更加均匀，取到最优解的效率比其他两种映射更高。此外，猫映射的初始取值可以为0或1。这特殊的性质是Logistic映射和Tent映射所不拥有的。因此，猫映射比其他两种映射拥有更好的混沌分布特性。由于混沌对初始值具备敏感的特性，可以扩大其搜索的范围，保证种群的多样性，避免出现局部最优的情况。

　　1.3 算法步骤

　　遗传算法[5]是一种随机搜索最优解的算法。对某个目标或对象，利用其对染色体的评价与对染色体中基因的作用，以及现有的信息数据来进行有效的改善和优化。基本遗传算法的步骤大体上可以分为6个阶段：

　　（1）随机生成一组初始种群，该初始种群由初始个体组成，同时需要评价每一个个体的适应度；

　　（2）判断算法是否满足收敛准则。若满足则输出搜索结果，否则执行下一步骤；

　　（3）根据每一个个体适应度的大小，以某种方式进行复制操作；

　　（4）按交叉概率Pc执行交叉操作；

　　（5）按变异概率Pm执行变异操作；

　　（6）返回步骤（2）。

　　混沌指的是一种确定但又不能预测的运动状态，它的非线性造成了系统的复杂性。混沌是不稳定性和随机性并存的运动状态，且由确定性方程得出。变量表现为混沌状态的可称为混沌变量。运动的不稳定性导致了混沌的不可预测性，因此混沌系统对无限小的初始值变动和微小扰动具有敏感特性。正因为混沌的优点，考虑混沌序列与基本遗传算法的组合，进而提出了混沌遗传算法。由于混沌序列对初始值的敏感特性，产生的种群不可能在某一时间处于同一局部极值，从而系统中进化不会停止。而在接近最优解时，由于混沌序列和家族竞争的共同作用，最优解总是持续地被更新，直到稳定于某个解值，搜索计算效率高[6]。

　　混沌扰动步骤如下：

　　（1）令Xij是待变异的第i个个体的第j个基因，取为[aj，bj]，运用公式A=（X-aj）/（bj-aj）映射到[0，1]区间得到混沌变量A。

　　（6）若算法运行时，出现了满足终止条件的情况，则此时，得到最优解x*并且输出，否则继续步骤（5）。

2 遗传算法参数的优化改进

　　为了解决基本遗传算法保持种群多样性差和容易陷入早熟的问题，引入了混沌序列。但是仅靠基本遗传算法与混沌序列的组合不能保证解的全局收敛性，因此基于猫映射的混沌遗传算法仍需要对遗传算法的几个方面进行优化改进。

　　通过猫映射函数产生的初始种群，其可以最大可能地均匀分布在解空间里，能解决随机序列产生初始种群的不均匀性问题，显著地提高了搜索性能。

　　交叉算子是遗传算法中非常核心的操作算子，影响着算法的搜索效率和性能。基本遗传算法设置了固定不变的交叉概率Pc。Pc的最佳取值随具体应用、种群分布和遗传进程而变化。而固定不变的Pc，由于不能提供合理正确的搜索方向，是引起最优个体和整个群体适应度改善速度以及搜索效率较低的重要原因。因此，引入自适应交叉概率可较好地解决该问题。一般情况下，交叉概率在0.4～0.99之间。这里对交叉概率进行如下改动：

　　遗传算法的进化后期，其种群非常接近于齐次种群。这时，种群难以产生新的子代个体，会出现“近亲繁殖”的现象。对于这样的问题，可以通过改变遗传算法的海明距离来维持种群的多样性，从而提高进化的效率。海明距离的表达式：

　　其中Hij是个体Xi、Xj的海明距离，H0是初始种群的平均海明距离。交叉方式按下式进行：

　　另外，遗传算法采用了2/4淘汰策略。交叉个体Xi、Xj与交叉产生的个体Xi、Xj、Xi′、Xj′在适者生存的条件下进行淘汰，然后选择其中适应度大的两个个体进行下一步的操作。其策略进行如下：

　　其中为[0，1]范围之间的随机数值。

　　通过对初始种群、自适应交叉率、海明距离以及淘汰策略的改进，加快了种群的进化速度，解决了遗传算法早熟和搜索精度低的问题，具有很高的搜索效率。

3 无源滤波器优化

　　3.1 参数的优化选择

　　对无源滤波器参数进行优化设计时，在满足基本设计原则[7]的基础上，需建立目标函数与约束条件两部分优化问题的数学模型。而无源滤波器参数优化设计其实是一个多目标优化的问题，因此需要从多个方面来建立无源滤波器参数优化的数学模型。

　　（1）无源滤波器的初期投资成本最小，即：

　　式（8）中，k1，k2，k3分别为无源滤波器的电阻Ri、电感Li和电容Ci（i表示无源滤波器组的序号）对应的单位价格（单位价格是依据无源滤波器中元器件允许通过的最大电流值和耐压值确定的，其能直接表明谐波的容量）；n为无源滤波器组的组数。

　　（2）在基波频率下，无源滤波器呈电容性，可以兼顾系统无功补偿的要求，吸收系统中大量存在的感性无功，提高功率因素，改善电能质量。按照基本的设计原则，无源滤波器装置一方面不能使系统出现无功功率过补偿的情况，另一方面又要使系统的功率因素尽可能地接近1，即：

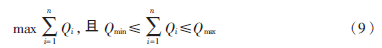
　　式（9）中，Qmin，Qmax分别是无源滤波器中的基波无功补偿的下限和上限。若出现，则系统会出现过补偿的情况。

　　（3）无源滤波器投入运行以后，应该保证电网的谐波含量控制在国家标准以内，并尽可能地低。为了简化分析，谐波电压和谐波电流含量均以总畸变率来表示，即：

　　式（10）和（11）中，THDU、THDI分别是谐波电压总畸变率与谐波电流总畸变率；U1、I1分别是基波电压与基波电流；Uhi、Ihi分别是第i次的谐波电压与谐波电流；THDUmax、THDImax分别是谐波电压总畸变率和谐波电流总畸变率的上限，其值一般依据国家标准计算得出。

　　因此，在一定约束条件成立的情况下，使得上面4个函数达到最协调的状态，从而得到最优解，这就是无源滤波器参数的多目标优化设计的核心思想。

　　3.2 工程实例研究

　　已知某系统参数如下：三相电压对称，系统基波电压6 kV，工频频率为50 Hz，负载最大有功功率为1.8 MW，实际功率因素为0.74。

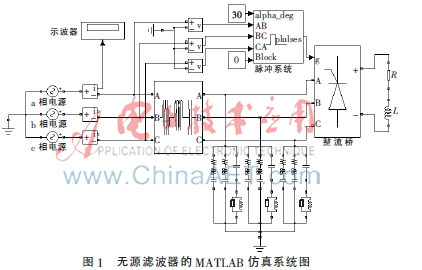
　　为了验证该无源滤波器优化设计方法的有效性，在MATLAB/Simulink软件环境下，建立了三相交流电网仿真系统模型，其中包括电网电源、非线性负载、无源滤波器装置等三部分。通过分析，其滤波支路主要包括5次单调谐滤波器、7次单调谐滤波器和9次高通滤波器。仿真模型如图1所示，其中，非线性负载采用三相六脉动不可控整流电路。

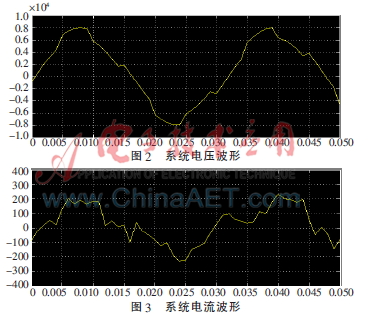
　　在无源滤波器装置未投入使用之前，系统电压和电流的波形如图2和图3所示。通过快速傅里叶变换分析，系统谐波电流的总畸变量为32.77%。

　　谐波指标和无功补偿是系统中无源滤波器装置运行时需要满足的条件。

参考文献

[1] SUH S， BASU A， SCHLOTTMANN C， et al. Low-power discrete fourier transform for OFDM： a programmable analog approach[J]. IEEE Transactions on Circuits and Systems I： Regular Papers， 2011，58（2）：290-298.

[2] 杨墨，邵定国，许路，等.基于FPAA的磁性防窃系统设计[J].电测与仪表，2009，46（12A）：107-110.