刘梅芷，柳晓鸣，索继东

　　（大连海事大学 信息科学技术学院，辽宁 大连 116026）

　　摘  要： 针对不同分布海杂波的抑制及目标检测问题，首次将自适应噪声对消器应用在海杂波的处理中，并且将此对消器与小波分解理论相结合来抑制海杂波，提取出目标。首先，对含有目标的海杂波信号进行小波分解。然后，类比自适应噪声对消器模型，设计一种自适应杂波对消器。将经小波分解后的信号作为自适应杂波对消器的输入信号，经过自适应杂波对消器输出的信号即为杂波抑制的结果。最后，通过MATLAB仿真，分析采用不同的小波基函数和不同的分解层数的杂波抑制效果，验证此种算法对于海杂波抑制的有效性。

　　关键词： 小波分解；自适应滤波器；杂波对消器；海杂波抑制；计算机仿真

　　0 引言

　　在航海雷达接收的信号中，通常包含雷达杂波信号和目标信号。如果没有杂波的干扰，雷达会很容易完成探测任务。同时，如果有杂波的存在，就会存在信杂比，这会影响到对目标信号的检测。尤其是在一些强海杂波背景中，由于目标信号很微弱，会淹没在海杂波中，所以对雷达杂波的抑制能力提出了更高的要求。雷达杂波抑制处理一直是雷达信号处理领域中的一个热门研究课题。目前，杂波抑制的方法有很多，但都未尽善尽美。因此，找出一种简单又实用的杂波抑制方法很重要[1]。

　　在雷达杂波中主要有四种杂波：海杂波、雨雪杂波、噪声和雷达同频干扰。其中，海杂波是最主要的干扰，它的相关性最强，所以是最难处理的杂波。

　　小波变换是一个时间和频率的局部变换，即在高频部分具有较高的时间分辨率和较低的频率分辨率，在低频部分具有较低的时间分辨率和较高的频率分辨率，这就使得小波变换具有对信号的自适应性。它能够有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析。适合用小波变换进行分析的信号应该具有不稳定性，尤其是对于那些急剧变化的高度不稳定信号效果较好。应用小波分解可以将杂波从含有目标的杂波中提取出来，但不是最佳的杂波成分估计。

　　本文首次采用了将小波分解与自适应滤波器相结合的方法来抑制杂波，类比于自适应噪声对消器设计了一个自适应杂波对消器，将含有目标的杂波作为自适应杂波对消器的主信道输入，将小波分解出的杂波成分作为参考信道输入。这样，输出信号即为杂波抑制结果。最后通过MATLAB进行实践仿真[2]。

　　1 基于小波分解的自适应滤波算法

　　1.1 海杂波信号的小波分解算法

　　在对雷达杂波信号进行小波变换时，必须对连续小波加以离散化。离散小波函数可写作：

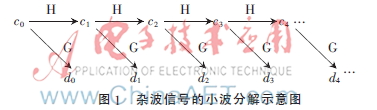
　　根据Mallat算法，对雷达杂波信号f（n）进行小波分解，可以得到信号的平滑项和信号的小波系数项，如图1所示。其中[3]：

　　经过小波分解后的平滑项表征雷达杂波信号中的各尺度的低频成分随时间的变化特性，即表征杂波的能量空间分布特性；小波系数项表征雷达杂波信号中的各尺度的高频成分随时间的变化特性，即表征杂波的方差成分。平滑项相当于雷达信号的低频成分，选择适当的尺度，便可以找到有效的抑制杂波的低频成分的处理方法；而小波系数项相当于雷达信号的高频成分，通过所提出的自适应对消方法，便可得到有效的抑制[4]。

　　1.2 自适应杂波对消器

　　通过分析自适应噪声对消器，对其进行类比推广得到自适应杂波对消器，这样就可以实现对杂波的抑制。

　　在自适应噪声对消器中噪声是需要消除的，通过去除噪声来逼近理想信号。然而在包含目标的海杂波中也有着类似的情况，需要想办法抑制甚至消除海杂波来得到理想目标。通过对比，将自适应噪声对消器加以改进可以得出自适应杂波对消器，如图2所示。图2中用作杂波补偿的参考输入n1进入自适应滤波器后输出y，经和主输入s+n0相减，得到系统的输出e=s+n0-y。如果n0=y，则系统的输出就是有效信号s；当n0与y十分相近时，系统的输出等于有效信号s与残余干扰量n0-y之和。为了使此残余干扰量达到最小，将系统的输出反馈到自适应滤波器。根据实际情况，选择合适的自适应滤波算法得到滤波器的权值，使得系统的总输出功率达到最小[5]。

　　1.3 自适应滤波算法的选择

　　自适应滤波的原理就是利用前一时刻已获得的滤波参数等结果，自动地调节现时刻的滤波参数，从而达到最优化滤波。其中，自适应滤波算法包括线性自适应算法和非线性自适应算法，非线性自适应算法具有更强的信号处理能力，但计算比较复杂，实际应用最多的仍然是线性自适应滤波算法。线性自适应滤波算法的种类很多，其中最小均方（Least Mean Square，LMS）算法和递归最小二乘（Recursive Least Square，RLS）算法比较典型，当研究中的信号是平稳随机信号时，采用LMS算法效果明显。而海杂波是非平稳信号，所以LMS算法很难自适应地跟踪统计特性变化的杂波干扰，因而其收敛效果一般。而基于RLS算法自适应滤波器克服了上述缺点，在非平稳环境下可以取得较满意的效果[6]。而由于雷达杂波信号具有非平稳特性，所以本设计采用RLS自适应滤波算法。在实验中，自适应滤波器的阶数为32，λ为0.98。

　　1.4 海杂波抑制模型

　　参考文献[7]指出，雷达信号小波变换的细节部分（高频部分）表征的是雷达杂波的方差特性，更能表现出杂波的浮动特性。所以，对信号进行小波分解，将分解后含有目标的杂波中的高频部分提取出来，作为自适应杂波对消器参考信道的输入，对其进行自适应滤波。最终，滤波器的输出结果即抑制杂波后的目标。杂波抑制模型如图3所示[8]。

2 海杂波的仿真及抑制

　　2.1 海杂波仿真

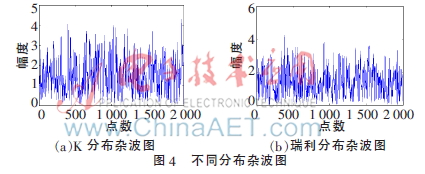
　　在仿真实验中，分别对服从瑞利分布的杂波和服从K分布的杂波进行抑制。首先，对这两种分布的杂波进行仿真，如图4所示。

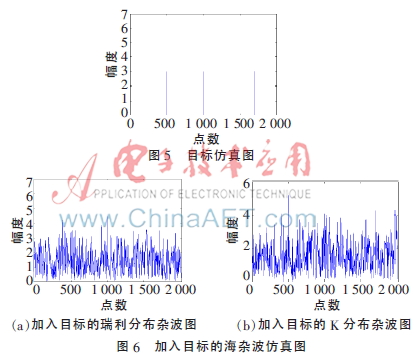
　　假设存在三个点目标，位置分别出现在500，1 000，1 700处，幅度均为3，如图5所示。将其加入仿真的杂波中，如图6所示[9]。

　　2.2 不同小波基杂波抑制效果比较

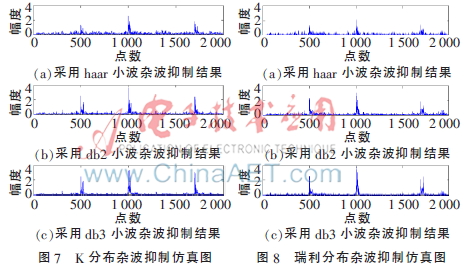
　　实验中分别采用haar、db2和db3小波。分别对K分布杂波和瑞利分布杂波进行抑制，结果如图7、图8所示[9]。通过对比可以看出，采用db2和db3小波的杂波抑制效果要优于haar小波。采用db2和db3小波来处理杂波并通过自适应滤波器都可以对杂波进行有效抑制，并可以准确检测出目标信号，只不过检测出目标信号的幅度稍有不同。同时此种方法同时适用于K分布和瑞利分布两种杂波。

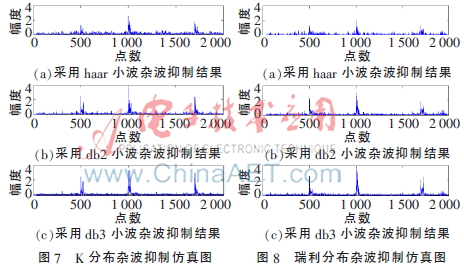
　　这说明小波分解出的细节部分（高频部分）可以大概表征杂波特性。同时在自适应杂波对消器中，采用的是RLS自适应滤波算法，这种算法适用于非平稳信号，而杂波信号就是非平稳信号。所以，通过小波分解与自适应杂波对消器的结合可以有效抑制杂波，检测出目标[10]。

　　2.3 尺度的选择

　　以db3小波为例，分别对尺度1、2、3下的杂波抑制效果进行比较。图9和图10给出了自适应杂波对消算法db3小波在尺度1、2、3下的杂波抑制效果图。

　　从图中可以看出，无论是K分布杂波还是瑞利分布杂波，在尺度为1时的杂波抑制效果是最好的。而当分解尺度大于3时，虽然杂波可以被有效抑制，但是目标也同时被抑制[11]。

3 结论

　　本文提出了一种将小波分解与自适应滤波结合来抑制海杂波的方法。通过对采用不同的小波基与不同尺度的结果进行对比分析得出，使用db3小波和1尺度可以得到很好的效果。结果表明，该方法能够有效抑制海杂波并且识别出目标。

　　参考文献

　　[1] 汤成霞，徐晓群，张荣涛，等.雷达杂波抑制的新方法研究[J].现代雷达，2012，34（9）：63-65.

　　[2] HAYKIN S.自适应滤波器原理[M].北京：电子工业出版社，2003.

　　[3] 吴永胜.小波变换在雷达信号处理中的应用[J].通信电源技术，2013，30（5）：84-89.

　　[4] 吴明，肖高清，王卫强，等.基于小波分解的自适应滤波算法及其应用[J].计算机仿真，2006，23（1）：105-107.

　　[5] 孙长生.VTS雷达杂波处理器的研究与设计[D].大连：大连海事大学，2005.

　　[6] 廖畅，山拜·达拉拜.基于自适应滤波的多模噪声抑制研究[J].计算机仿真，2012，29（4）：189-192.

　　[7] REYES J A T. DSP-based oversampling adaptive noise canceller for background noise reduction for mobile phones[J].Electrical Communications and Computers，2012，5（30）：327-332.

　　[8] 柳晓鸣.子波变换用于VTS雷达杂波抑制的研究[D].大连：大连海事大学，1999.

　　[9] 朱洪俊.非平稳信号自适应滤波的小波模型与滤波方法[J].机械工程学报，2006，42（8）：201-204.

　　[10] 陈鲲，陈云秋，陈世友.海杂波建模与仿真[J].舰船电子工程，2009，29（2）：95-98.

　　[11] 苏昭斌，陈红卫.海杂波复合K分布模型的参数估计[J].计算机应用与软件，2014，31（8）：273-275.