张强
(中国科学技术大学 自动化系,安徽 合肥 230027)
摘要:标准HOG模型在行人检测领域中最为经典,相比于标准模型中整齐划一的block,不同尺寸的block可以获得更多的细节信息。首先,在去除上下文背景的32×96尺寸模型基础上设计144个block特征;然后,提出类Fisher比计算block类别区分力;最后,利用NMS方法选出24个block,串接为1 854维的行人检测模型。实验结果表明,该利用特征选择改进的行人检测模型获得了显著的性能提升。
关键词:行人检测;特征选择;线性判别分析;非极大值抑制
0引言
行人检测是计算机视觉热门研究领域之一。人体的非刚体性、外观多样性、复杂背景、光照变化、尺度变化、遮挡等研究难点给行人检测研究提出了巨大的挑战。另一方面,行人检测的市场应用前景十分广阔,典型应用有智能视频监控、车辆辅助驾驶行人保护系统、智能交通控制等,近年来也应用到航拍图像、受害者营救等新兴领域[1]。
本文在32×96尺寸下,设计了144个不尽相同的block特征,然后利用一种新颖的特征选择方法从中挑选出24个,将这些特征向量串联构成一个1 854维的行人检测模型,最后用线性支持向量机进行模型训练。实验结果表明,利用特征选择改进的行人模型显著提升了检测性能。
1相关工作
DALAL N和TRIGGS B在2005年CVPR上提出HOG特征[2],3 780维的64×128标准HOG行人模型近乎完美地解决了MIT行人数据集[3],文中一并推出更具挑战性的INRIA Person数据集。
针对标准HOG行人模型内部block尺寸单一、简单地将block特征串联而不能充分发挥HOG潜力的问题,Zhu Qiang等人[4]将block尺寸从典型的16×16中释放出来,通过改变block的宽高比例以及block在窗口内部的滑动步长等,获得5 031个不尽相同的block。每一个block结合SVM训练得到一个弱分类器,最终用AdaBoost方法从这些弱分类器中选择构建级联结构的分类器。该方法不足之处在于:在FPPW(False Positives Per Window)vs漏检率的评价方法下,级联HOG在漏检率较大时的性能表现依然不如标准HOG行人模型;尽管可以从5 031个block中做出随机选择,但是训练数以百计弱分类器的工作量依然十分巨大。
田仙仙等人[5]在标准HOG行人检测模型的基础上,通过改变block中cell大小,设计了3种不同尺寸共计21个block特征,然后利用Fisher准则给所有特征排序,将类间离散度矩阵与类内离散度矩阵之间行列式比值衡量block特征的区分能力,比值越大表示block区分力越强,最后挑选block直到满足设定的分类准确率要求。作者利用这种方法选择出10个block,特征向量合计360维。但是,作者采用从多种不同渠道获得的随机混合样本,并没有在完整的INRIA Person数据集上做出Multi HOG的性能对比。同时,Zhu Qiang等人[4]和田仙仙等人[5]均没有在FPPI vs漏检率[6]的评价方法下做出性能评价。
特征选择是从一系列特征中挑选出最有效的特征以降低特征空间维度的过程,其目标是寻找一个最小特征子集,该子集以较高程度的正确性代表原始的特征集合。特征选择算法[78]按照特征集合评价策略可以划分为过滤式(Filter)和封装式(Wrapper)两大类。
Filter与Wrapper方法的区别在于对特征子集的评价是否用到机器学习算法。其中,Wrapper方法将筛选出来的特征直接进行分类器训练,然后根据分类器在验证集上的表现来评价该特征子集。这类方法的优点在于能够有效地辨识关键特征,挑选出规模相对较小的特征子集,精简学习机器的结构;缺点同样明显,由于需要反复不断地训练和测试分类器,这类方法一般比较耗时。Filter方法对特征子集的评价不需要经过机器学习算法的训练,是一类计算效率相对较高的方法。相对Wrapper方法,Filter方法对关键特征的寻找会有一些阻碍,但其能够去除大量非关键性的噪声特征,可以帮助找到次优的特征子集。
本研究的数据类型与样本数量决定了无法采用代价过大的Wrapper方法。Filter方法采用了概率距离和相关距离法、类间与类内距离测量法、信息熵法、决策树滤波等评价方法。结合本文样本数据特点,本文主要考虑类间与类内距离测量法。
线性判别分析(Linear Discriminant Analysis, LDA)通过寻找一个转换矩阵W,将原始数据空间转换为维度更低的特征空间,并使得类间离散度和类内离散度的比值最大,离散度测度用样本离散度矩阵的行列式值计算,目标函数如下:

其中,SB表示类间离散度矩阵,SW表示类内离散度矩阵。一般情况下,转换矩阵可以通过求解S-1WSBW=λW获得。
崔自峰等人[9]在LDA的基础上提出受限线性判别分析。受限LDA完成的特征选择没有对特征进行转换或组合,不改变特征语义,保留了原始数据的可理解性,其转换矩阵为一个二值矩阵,转换矩阵的每一列有且仅有一个非零元素1,表示对原始特征空间中某一个维度的选择。而且针对类内离散度矩阵SW奇异,传统求解特征方程组的方式不再适用,作者将离散度的测度由行列式值替换为矩阵的迹,目标函数修正为:
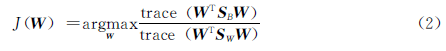
结合二值转换矩阵,参数文献[9]用![D(O]}QD9I6MON{HQZ]7M48L.jpg D(O]}QD9I6MON{HQZ]7M48L.jpg](http://files.chinaaet.com/images/2016/03/21/6359418671545811266001527.jpg) 表征相应特征的评价分数,挑选所有比值大于1的特征,或者遵循经典的特征选择,通过预先给定k值,只选择前k个特征。很明显,如何确定k值是一个棘手的问题。此外,受限LDA没有对选中的特征之间进行去冗余操作,选中的特征中很可能彼此有很高的相似度。
表征相应特征的评价分数,挑选所有比值大于1的特征,或者遵循经典的特征选择,通过预先给定k值,只选择前k个特征。很明显,如何确定k值是一个棘手的问题。此外,受限LDA没有对选中的特征之间进行去冗余操作,选中的特征中很可能彼此有很高的相似度。
王飒等人[10]针对高维数据提出了一种基于Fisher准则和特征聚类的特征选择方法。首先利用单个特征的Fisher比来衡量特征的类别区分力,并依据Fisher比对特征降序排序;然后累加所有特征的Fisher比,设定预选累加和占比ρ,预选出类别区分力较强的特征子集;最后利用相关系数度量特征之间的冗余度,在预选的特征子集上对特征进行分层聚类,从每一个聚类中选择Fisher比最大的一维特征加入最终的特征子集,以达到去冗余的目的。
2改进的行人检测模型
本文采用在64×128标准HOG行人模型基础上去除上下文背景的32×96尺寸模型。
2.1特征设计
Fast HOG[4]和Multi HOG[5]均延续了由2×2 cell构成block的做法,用9个方向统计cell的梯度方向直方图,所以每个block特征均为36维。考虑cell尺寸过大将无法有效获取图片的细节信息,于是本文采用与上述不同的设计方案:将cell的尺寸保持为8×8,只在block的cell组合上做出变化。
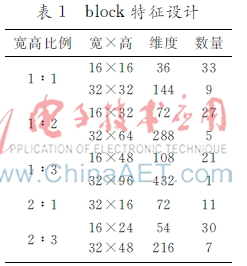
在32×96滑动窗口内,将block宽度限定为16和32,宽高比例从1∶1、1∶2、1∶3、2∶1变化到2:3,相邻block移动步长为8,如表1所示,设计了144个共9种不同尺寸的block。表1block特征设计宽高比例宽×高维度数量1∶116×16363332×3214491∶216×32722732×6428851∶316×481082132×9643212∶132×1672112∶316×24543032×482167如图1所示,每一个方格代表一个8×8 cell,32×96的滑动窗口包含48个cell。如表2所示,第1个16×16 block由1/2/5/6这4个cell组成,第2个16×16 block由2/3/6/7这4个cell组成,第1个32×32 block由1/2/3/4…13/14/15/16这16个cell组成,依此类推。


2.2类Fisher比
本文采用Filter方法进行特征选择。但是,Filter方法一般判断是否选择特征向量中的某一维,而本文的特征集合由144个block组成,如表1所示,这些block特征均不是单一维度。因此黄仙仙等人[5]用Fisher比衡量block的类别区分力,首先计算训练样本的类间离散度矩阵SB和类内离散度矩阵SW:
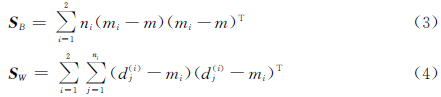
其中,mi表示第i类样本的特征向量均值,m表示两类样本合在一起的特征向量均值: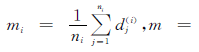
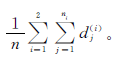 。
。
然后计算block的Fisher比: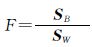 。
。
虽然协方差矩阵为半正定矩阵,所有特征根非负,但是依然存在0值特征根的风险,从而导致离散度矩阵行列式为0。事实上,从本文的实验过程来看,训练样本的类间离散度矩阵SB行列式值为0,是奇异矩阵。而一旦|SB|=0,Fisher比将无法衡量该block的类别区分力。
为了避免0值特征根的风险,崔自峰等人[9]和王飒等人[10]在对单一维度特征进行选择时,用训练样本集上的类间方差和类内方差的比值来度量该维特征的类别区分力。结合本文特征数据类型,将其扩展为样本类间离散度矩阵的迹与类内离散度矩阵的迹之间的比值,用离散度矩阵特征根的和替代特征根的积,从而得到block特征的类别区分力,称为类Fisher(Fisherlike)比:

类Fisher比越大,block的类别区分能力越好。
2.3NMS特征选择
图2NMS特征选择流程依据各block在训练样本集上的类Fisher比,可以得到有序的全体特征集合。如果遵循传统的特征选择方法,只选择前k个block,那么存在一个严重问题:训练样本中目标某些部位的cell具有非常显著的类别区分力,导致包含这些cell的block特征也具有较高的区分力得分。显然,对cell过多地重复利用,将造成特征严重冗余。因此,本文提出了一种非极大值抑制(NonMaximum Suppression, NMS)方式的特征选择方法。
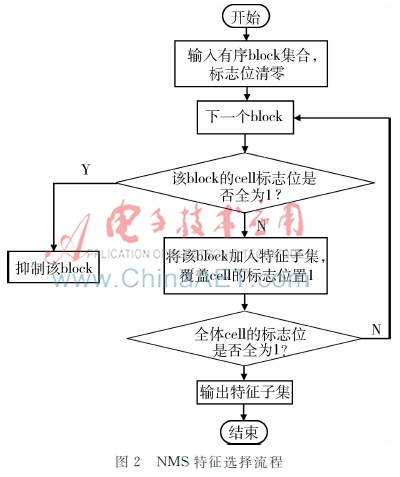
如图2所示,首先依据block的类Fisher比值进行排序,得到有序的全体block特征集合,并且给每一个block设置标志位,标志位为0表示此cell没有被block占用,标志位为1表示此cell已被占用;然后从类Fisher比值最大的block开始,标记占用的cell,并将其加入特征子集;再输入下一个得分较低的block,如果该block占用了未标记的cell,那么将该block加入特征子集,并将新占用的cell标记为1,如果构成该block的所有cell标志位均为1,则抑制该block;循环执行上一步,直到全体cell标志位均为1停止。最后,输出特征子集。
与王飒等人[10]特征聚类的目的类似,本文NMS方法也是为了在保证特征子集类别区分力的基础上进行特征去冗余。
本文提出的结合类Fisher比计算类别区分力和NMS选择特征子集的特征选择方法,既保持了特征语义,又实现了在合理代价下获得次优的特征子集。
3实验分析
本文以INRIA Person数据集作为验证平台,训练集由2 416张裁剪好尺寸的正样本和1 218张负样本图片组成,测试集由288张共包含589名行人目标的图片组成。
首先分别在正负训练样本中提取全部144个block特征数据,随机从负样本图片中选择10个窗口,组成12 180个负样本。然后计算各block的类间离散度矩阵SB和类内离散度矩阵SW。如前文所言,从16×16 block开始计算SB的行列式,但33个block结果全部为0,而且SW的行列式值也极大,常溢出而被视为正无穷,这些均会导致block的Fisher比为0,这也是本文无法用Fisher比衡量block类别区分力的直接原因。因此提出类Fisher比,继续利用SB和SW计算各block的类Fisher比值,并将全体block按类Fisher比值降序排序。最后利用NMS从144个block中选择出24个特征,如表3所示,涵盖6种尺寸,合计1 854维。

值得说明的是,本文特征选择的结果与训练集正样本间的对称性保持一致:1 208个目标经由镜面对称处理得到翻倍的2 416张正样本,而表3中的block之间也保持了左右对称。
明确特征子集之后,从训练样本中提取这24个block的特征向量,串接成1 854维。然后利用线性支持向量机进行模型训练,误分类代价设为[0,1;1,0],其间搜寻了2轮的困难样本,并将困难样本加入初始样本集中重新训练,得到最终的分类器。最后基于FPPI vs漏检率的评价方法,在INRIA Person测试集上检验模型的性能。
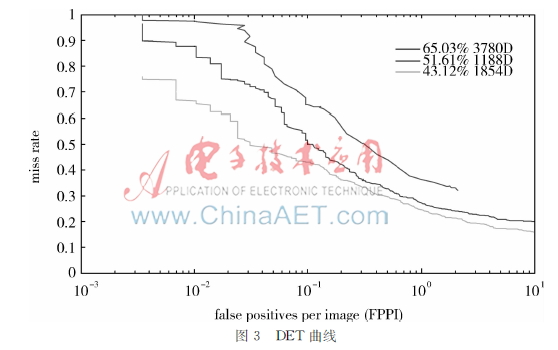
如图3所示,DET曲线越低表示性能更好[6],上方的性能曲线对应3 780维的标准HOG行人模型;居中的性能曲线对应1 188维去除上下文背景的32×96模型;下面的性能曲图3DET曲线

线对应本文1 854维的利用特征选择改进的行人检测模型。显而易见,上述模型的性能依次递增,以01FPPI为例,三条曲线的漏检率分别为6503%、5161%以及4312%。
如图4示例,(a)、(b)、(c)分别为标准HOG行人模型、去除上下文背景行人模型以及利用特征选择改进的行人检测模型对同一张图片的检测结果,显然,检测效果是依次递增的。
4结论
本文还存在以下问题:block设计上可以更丰富一些,可以将改变cell尺寸来设计block的方式与本文的方式相结合;本文的特征选择方法得到的是一个次优的特征子集,未来可以继续研究具备可行性的寻找最优特征子集的方法。
参考文献
[1] 苏松志, 李绍滋, 陈淑媛, 等. 行人检测技术综述[J]. 电子学报, 2012, 40(4): 814820.[2] DALAL N, TRIGGS B. Histograms of oriented gradients for human detection [C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA: IEEE Press, 2005, 1: 886893.
[3] PAPAGEORGIOU C, POGGIO T. A trainable system for object detection [J]. International Journal of Computer Vision, 2000, 38(1): 1533.
[4] Zhu Qiang, AVIDAN S,YEH M C, et al. Fast human detection using a cascade of histograms of oriented gradients[C].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA: IEEE Press, 2006, 2: 14911498.
[5] 田仙仙, 鲍泓, 徐成. 一种改进HOG特征的行人检测算法[J]. 计算机科学, 2014, 41(9): 320324.
[6] DOLLáR P, WOJEK C, SCHIELE B, et al. Pedestrian detection: A
benchmark[C]. IEEE Conference on Computer Vision and Pattern Recognition. Miami, Florida, USA: IEEE Press, 2009: 304311.
[7] 毛勇, 周晓波, 夏铮, 等. 特征选择算法研究综述[J]. 模式识别与人工智能, 2007, 20(2): 211218.
[8] 姚旭, 王晓丹, 张玉玺, 等. 特征选择方法综述[J]. 控制与决策, 2012, 27(2): 161166.
[9] 崔自峰, 吉小华. 基于线性判别分析的特征选择[J]. 计算机应用, 2009, 29(10): 27812785.
[10] 王飒, 郑链. 基于Fisher准则和特征聚类的特征选择[J]. 计算机应用, 2008, 27(11): 28122813.

