周小明1,陈 刚1,杨宏宇2
(1.国网辽宁省电力有限公司,辽宁 沈阳110006;2.南瑞集团公司信息通信技术分公司,江苏 南京210003)
摘 要: 本文研究了电力企业指标的数据形态和业务形态,确定指标数据在一定时间阶段内是否稳定(业务是否稳定),发现指标在时间序列的变化特征,以及观察指标数据在每个时间周期内是否呈线性趋势,应用统计学及数据挖掘方法,结合业务的精细化需要,提出了适用于不同特性指标的三种阈值设置方法,包括正态分布指标阈值设置方法、时间序列指标阈值设置方法以及线性拟合指标阈值设置方法。实验结果表明,本文提出的三种阈值设置方法能够反映业务实际,对国家电网的运营监测有着重要意义。
关键词: 数据挖掘;正态分布;时间序列;线性拟合;阈值设置
0 引言
国家电网运营监测中心对各业务部门进行指标数据监测的主要根据是业务专家知识和经验[1-2],所以对专家的业务水平有很大的依赖性。本文将数据挖掘的方法引入到电力企业指标阈值设置的研究领域,用时间序列模型反映数据时间变化特征[3-5],用正态分布反映数据的稳定性[6-7],用线性拟合体现数据的线性变化趋势[8],在一定程度上解决了以往设置的阈值缺少客观依据的现状。
1 指标阈值设置方法
本文介绍了三种指标阈值设置方法,包括正态分布方法、时间序列方法、线性拟合方法,其中涉及到的正态分布有效性检验、时间序列建模条件检验和模型创建,以及线性拟合均采用工具Pluto数据挖掘平台实现。
1.1 正态分布
1.1.1 正态分布算法介绍
正态分布是实践中应用最为广泛、在理论上研究最多的分布之一,它在概率统计中占用特别重要的地位。
正态分布的概率密度函数为:

正态分布的3规则如图1所示,置信区间如表1。


1.1.2 正态分布指标阈值设置方法
正态分布指标阈值设置方法,首先需要判断指标数据是否符合正态分布,若符合正态分布,则选取最近周期的指标数据作为分析对象,计算该样本数据的均值与标准差,根据正态分布置信区间的覆盖率,结合业务的精细化需要,上下限围绕中心点(均值)做2个标准差的波动形成指标阈值。
1.1.3 适用于正态分布阈值设置方法的指标特性
(1)在一段较长时间周期内(1年以上),业务是稳定的、收敛的。数据呈现出来的形式是趋近与某一点,并在一定范围内波动。
(2)在正态分布有效性检验中P值>0.05时,说明样本数据符合正态分布形态。
(3)适用于服从正态分布的数据。
(4)受连续时间因素干扰较小。
1.2 时间序列
1.2.1 时间序列算法介绍
时间序列法是一种定量预测方法,在数据挖掘中作为一种常用的预测手段被广泛应用。对时间序列建模的两个任务,一是分析当期数据如何受前几期的数据影响,二是变量在时间变化上的规律性。
本文选用的时间序列算法为ARIMA算法。
ARIMA模型是将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。在ARIMA模型的识别过程中,主要用到两个工具:一是自相关函数(简称ACF),二是偏自相关函数(简称PACF)以及它们各自的相关图(即ACF、PACF相对于滞后长度描图)。对于一个序列y来说,它的第k阶自相关系数(记作rk)定义为它的k阶自协方差除以它的方差。

它是关于k的函数,因此也称之为自相关函数,通常记为ACF(k)。偏自相关函数PACF(k)度量了消除中间滞后项影响后两滞后变量之间的相关关系。
ARIMA(p,d,q)模型是经过d阶差分变换后的ARMA(p,q)模型,ARMA(p,q)模型的一般形式:
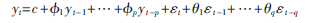
ARIMA(p,d,q)模型的算法如下:
(1)对原序列进行平稳性检验,如果序列不满足平稳性条件,可以通过差分变换(单整阶数为d,则进行d阶差分)或者其他变换,如对数差分变换使序列满足平稳性条件。
(2)通过计算能够描述序列特征的一些统计量(如自相关系数和偏自相关系数),来确定ARMA模型的阶数p和q,并在初始估计中选择尽可能少的参数。
(3)估计模型的未知参数,并检验参数的显著性,以及模型本身的合理性。
(4)进行诊断分析,以证实所得模型确实与所观察到的数据特征相符。
1.2.2 时间序列指标阈值设置方法
时间序列指标阈值设置方法,首先需要对时间上连续的指标数据进行时间序列建模条件检验,如果数据既满足平稳性,又具有相关性,则应用ARIMA算法对样本数据进行ARIMA时间序列建模,对模型性能进行评估,若模型可用,则以模型创建过程中形成的样本预测数据与实际数据的偏差为分析对象,计算其误差均值与误差标准差,根据正态分布置信区间与样本覆盖率的对照关系,结合业务的精细化需要,上下限围绕指标当前预测值做2个标准差的波动形成指标阈值。
1.2.3 适用于时间序列阈值设置方法的指标特性
(1)当指标数据或者一阶差分平稳性检验<0.05,且检验模型中数据存在自相关和偏自相关性(相关性检测图中,存在自相关系数、偏自相关系数超出±2倍估计标准差)时,说明样本数据适合时间序列算法。
(2)适用于连续时间点数据序列,当数据因为数据质量出现缺值时应对数据进行预处理后才能使用时间序列。
(3)不适用与在连续时间序列中出现多个异常点的情况。
1.3 线性拟合
1.3.1 线性拟合算法介绍
若两组数据X和Y具有统计关系而且是线性关系,那么就可以建立回归模型:
 。
。
1.3.2 线性拟合指标阈值设置方法
线性拟合指标阈值设置方法是,首先需要观察指标历史数据的变化趋势,如果数据在每个时间周期内呈线性趋势,并且不同时间周期数据的变化趋势近似相同,则对每个时间周期内的数据分别应用线性拟合算法进行一元线性回归,若拟合度R2都大于0.95,则选择最近时间周期内的数据及线性拟合函数,以该样本预测数据与实际数据的偏差为分析对象,计算其误差均值与误差标准差,按正态分布置信区间与样本覆盖率的对照关系,结合业务的精细化需要,上下限围绕指标当前预测值做3个标准差的波动形成指标阈值。
1.3.3 适用于线性拟合阈值设置方法的指标特性
(1)在每个时间周期(一般选择1年为一个周期)内,业务是稳定的。数据在每个时间周期内呈线性趋势,并且不同时间周期数据的变化趋势近似相同(即不同时间周期内同一时间点的指标值几乎相同)。比较适用于指标的累计值。
(2)对每个时间周期内的数据进行线性拟合,拟合度R2都需大于0.95。
(3)适用于具有线性趋势的数据。
(4)受连续时间因素干扰较小。
2 实验结果及分析
本次实验在选取数据时,依据运营监测指标体系中的指标项,采用某省电力公司的3个指标的省数据作为研究对象,运用以上介绍的三种指标阈值设置方法进行实验分析。指标清单如表2。

2.1 基于正态分布方法的“总资产周转率”阈值设置
2.1.1 指标数据进行正态分布分析
选取总资产周转率当期值,2012年1月到2012年12的样本数据进行正态性分布检测,共计12条数据。利用正态分布校验模型分析,其显著性指标P=0.754,P值大于0.05,说明服从正态分布。校验图如图2。

2.1.2 波动区间计算
以正态分布置信区间与分布覆盖率对照表为依据,以保证95%的样本值落入域值范围作为异动监测要求。
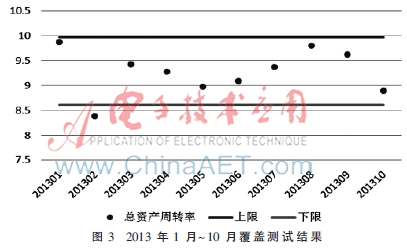
利用正态分布统计分析模型,计算所提供的2012年的12条样本数据的均值与标准差。均值为:9.291,标准差为:0.339,按上下限围绕中心点做2个标准差的波动形成指标阈值。可计算得到总资产周转率上限为:9.970,下限为:8.613。
按照上述2012年数据得到的阈值,对2013年1月到10月数据(共10条数据)进行覆盖率测试,如图3所示。
2.2 基于时间序列方法的“单位购电成本”阈值设置
选取单位购电成本当前值,2008年1月到2013年9月省数据,共计69条数据(其中,2013年3月和4月数据为空)。以2008年1月~2013年2月的数据为时间序列模型使用的样本数据,包括模型构建样本数据(2008年1月~2012年12月的数据)与测试数据(2013年1月和2月的数据),共计62条记录。
2.2.1 样本数据检验
(1)数据的平稳性检验
应用检验模型得到P=0.951 5,说明该数据是一组非平稳序列。
对原数据进行一阶差分处理,对差分后的数据再次进行平稳性检验,P=0.000 0,此时数据具有平稳性。说明原数据具有一阶平稳性。
(2)数据的相关性检验
对一阶差分后的数据进行相关性检验,具有相关性(包括自相关和偏自相关)。相关性检验如图4所示。

从检验结果可以看出,此时数据存在自相关和偏自相关性(相关性检测图中,序列1阶自相关系数、1阶偏自相关系数均比较显著,具有自相关性)。因此,该数据可进行时间序列建模。
2.2.2 时间序列建模
选取2008年1月~2012年12月的数据作为时间序列建模的训练样本,2013年1月和2月的数据作为测试样本。时间序列如图5所示。

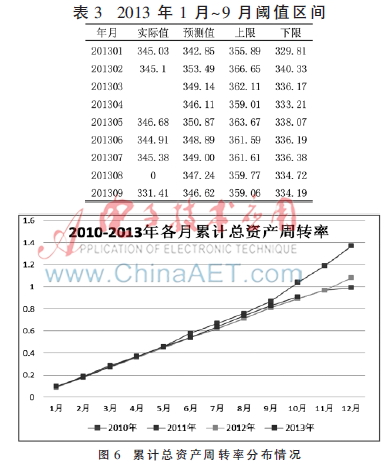
以ARIMA时间序列模型为预测模型,获得2013年1月和2月时间序列预测结果与实际数据比对误差如表3。
2.2.3 波动区间计算
上述时间序列模型的误差的均值为0.139 2,误差的标准差为:6.520 4。应用时间序列模型,实时地预测2013年1月~2013年9月各月单位购电成本。并根据设置指标波动区间的方法,设置各月指标的阈值区间,如表3。
2.3 基于线性拟合方法的“累计总资产周转率”阈值设置
2.3.1 指标数据线性拟合分析
选取总资产周转率累计值,2010年1月~2013年10月省数据,共46条。该指标数据在一年内(12个月)呈线性增长的趋势,并且每年的变化趋势近似相同。2010年~2013年各月数据的分布情况如图6所示。
对2010年、2011年、2012年的数据(每年12条数据)分别按照月份进行线性拟合,2010年、2011年、2012年的数据线性拟合的拟合优度均大于0.95,说明“总资产周转率”指标的累计值在一年内呈线性增长趋势,并且在每年的同月指标值几乎相同。
2.3.2 波动区间计算
选取2012年各月数据得到线性拟合函数,计算2012年各月的预测值,同时以该样本数据的预测值与实际数据的偏差为分析对象,计算其误差均值与标准差。
经计算得到误差的均值为0.000 258,误差的标准差为:0.005 931。应用以上线性拟合函数,预测2013年1月~2013年10月辽宁各月累计总资产周转率值,并根据设置指标波动区间的方法,设置各月指标的阈值区间。
3 结论
本文根据国家电网的运营监测中心对于指标的监测有较多指标阈值设置是由业务专家人工设置实现的现状,针对存在部分指标设置没有结合各地区业务能力的差异,或者没有充分考虑业务自身规律等问题,通过研究指标的数据形态和业务形态,确定指标数据在一定时间阶段内是否稳定(业务是否稳定),发现指标在时间序列的变化特征,以及观察指标数据在每个时间周期内是否呈线性趋势,结合统计学及数据挖掘方法,提出了适用于不同特性指标的三种阈值设置方法——时间序列指标阈值设置方法、正态分布指标阈值设置方法以及线性拟合指标阈值设置方法。在此基础上,应用本文提出的方法对相适用三类指标进行了实验和分析,并将通过线性拟合方法得到的“累计总资产周转率”的阈值和目前国网已有的阈值进行了对比实验。实验结果表明本文的方法设置的指标阀值更加合理,更能反映客观现实情况。
参考文献
[1] 张云飞.我国电力行业运行情况剖析[J].上海电力,2008(6):519-524.
[2] 国家电网公司总部运营监测(控)中心建成投运[J].电力信息化,2013(6):111-112.
[3] 段江娇.基于模型的时间序列数据挖掘[D].上海:复旦大学,2008.
[4] 谷赫.时间序列的数据挖掘在证券预测分析中的应用研究[D].长春:吉林大学,2005.
[5] 李庆雷,马楠,付遵涛.时间序列非平稳检测方法的对比分析[J].北京大学学报(自然科学版),2013(2):252-260.
[6] 马莉.电力市场环境下发电公司报价策略研究[D].杭州:浙江大学,2003.
[7] 杜宇上.基于正态密度函数的滚动窗口路径规划方法[J].科学技术与工程,2010(15):3741-3744.
[8] 何菊明,王芙.实验数据的线性拟合及计算机处理[J].武汉工程大学学报,2008,30(1):117-119.

