文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.03.011
中文引用格式： 尹培培. 非精确浮点数乘法器设计[J].电子技术应用，2016，42(3)：38-41，46.
英文引用格式： Yin Peipei. Design and analysis of inexact floating-point multiplier[J].Application of Electronic Technique，2016，42(3)：38-41，46.
0 引言
目前，集成电路的设计工艺已经进入深亚微米阶段，工艺水平大幅度提高，计算机微处理器也不断更新换代。在微处理系统中，数据类型分为定点数和浮点数，相对于定点数的有限范围及有限精度，浮点数可以灵活地表示更大范围及更高精度的实数，由于以上原因，浮点数运算成为微处理器以及信号处理系统中的重要部件之一。但同时相对于定点数而言，浮点数运算需要更复杂的硬件电路，消耗更大的面积及能量，因此为数据范围的拓宽带来了能量及面积上的消耗。传统的电路设计大多运用精确计算算法，但对于一些图像处理的可容错应用，这些系统并不需要绝对的精确性。所以将非精确运算[1]运用到这些系统中可以减小能量损耗及电路面积，同时也可提高系统的性能。
非精确的算法设计作为减少容错设备的动态及静态能量损耗的有效方法，它的主要思想是通过减小硬件的复杂度来提高系统的性能及效率。目前非精确计算主要集中在定点数的研究[2-5]，文献[2]中非精确处理器牺牲了7.58%的相对错误率，但速度、面积比精确处理器速度提高了将近15倍，能量损耗也减少了将近15倍。研究表明运用非精确算法设计出的芯片面积更小，速度更快，能量损耗更低。虽然定点数在非精确研究方面取得了较成功的应用，但相对于定点数而言，目前对非精确浮点数运算的研究并不多。由于浮点数运算电路更复杂，能量也消耗更多，非精确浮点数算法的研究显得尤为重要。
文献[5]设计了一种非精确的浮点数加法器，该设计通过将低位部分精确加法替代为或门算法实现非精确运算；文献[6]研究了一种低功耗的浮点数乘法器，该研究通过直接截断浮点数的数值位来减少硬件；文献[7]设计了一种高效率的浮点数乘法器；文献[8]利用低精度浮点数来减小MP3解码时的内存损耗。
本文提出了一种非精确浮点数乘法器的算法设计，同时将该算法应用于高动态范围图片的图像处理中，并将结果与精确浮点数乘法器的应用结果进行对比。文章内容分布如下：在第1节中，首先简单介绍了浮点数构成及精确的浮点数乘法器的结构；在第2节中提出了非精确乘法器的设计方法；在第3节中将该非精确乘法器应用到高动态范围图片中；最后总结了该设计算法。
1 背景简介
1.1 浮点数表示方法
在算数运算中，数据的表示方法有两个，定点数和浮点数。定点数可以表示以0为中心的一定范围的正负整数，由于定点数小数点固定，不能表示太大动态范围的数，同时也不能表示过大或过小的数，此时浮点数的优势就体现了出来，它可以在不增加位数的前提下扩展数据的动态范围。
在IEEE 754-2008标准中，浮点数是一个以3个量表示的二进制位串(如图1所示)，该位串分为3个部分：符号位部分、指数位部分和尾数位部分。
浮点数的标准表达式为：
其中，S为符号位，当S=0时表示该浮点数是一个正值，当S=1时表示该浮点数是一个负值；E为指数位，bias表示偏移量，对于单精度bias=127，双精度bias=1023，则E-bias既可为正数也可为负数；M为尾数位，对于规格化的尾数，存储时默认省去小数点前的1，则对于非零尾数，尾数值为1.M。
1.2 精确浮点数乘法器
最初的浮点数乘法器是依靠软件实现的，但随着超大规模集成技术的发展以及乘法器对计算速度要求的提高，乘法运算逐渐变成一个硬件的部件，浮点数乘法的基本原理是将相乘两数的指数和作为乘积的指数，相乘两数尾数的积作为乘积的尾数，相乘两数的符号位异或作为乘积符号位。
精确的浮点数乘法器如图2所示，默认这里两个操作数都已规格化，如若没有，则首先需将输入的操作数规格化。然后从两操作数中分别提取每个操作数的符号位、指数位及尾数位，并将尾数位补充省略的第一位1。浮点数的乘法只要包括两个运算：指数的加法和尾数的乘法，这两运算结束后就是将结果进行规格化，生成符合IEEE 754-2008标准的结果。
2 非精确浮点数乘法器设计
非精确乘法器的设计是基于图2所示的精确计算的算法级设计，主要是将非精确定点数乘法器运用到浮点数尾数乘法设计中，同时考虑到尾数乘积已是非精确结果，舍入单元及规格化也进行了简化。
2.1 尾数乘法器
尾数乘法器就是计算两个浮点数尾数部分的乘积，也就是两个无符号定点数的乘法，主要包括3个部分：部分积的生成、部分积压缩及最终结果的生成。本文部分积通过非精确Booth编码[9]生成，部分积压缩通过非精确4-2压缩器[10]及Wallace树[11]完成。对于单精度浮点数，尾数的乘法是无符号定点24×24位的乘法器，修正Booth编码产生了13个部分积；4-2压缩器、Wallace树以及进位存储加法器将部分积压缩成2个操作数；最后48位和进位采用快速超前进位加法器相加。
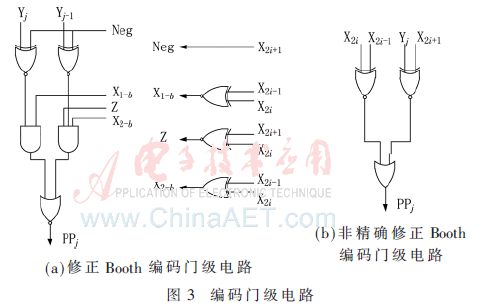
非精确Booth编码是在修正Booth编码算法上改进的，修正Booth编码算法的门级电路如图3(a)所示，式(2)给出了部分积（Partial Products，PP）与输入之间的关系。非精确Booth编码的门级电路如图3(b)所示，式(3)给出了部分积与输入之间的关系。
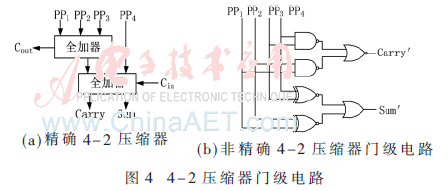
部分积的压缩通过4-2压缩器实现，非精确压缩器是在精确4-2压缩器上改进得到，精确4-2压缩器的实现方法如图4(a)所示，式(4)~式(6)给出了压缩结果与部分积输入之间的关系。非精确4-2压缩器的实现方法如图4(b)所示，式(7)~式(8)给出了压缩结果与部分积输入之间的关系。
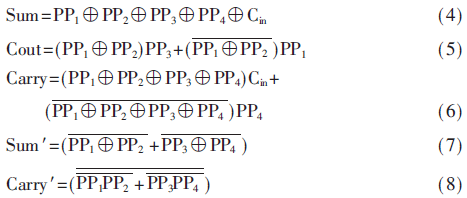
以单精度浮点数为例，非精确尾数乘法器的Wallace树结构如图5所示，由于最终标准化后只取乘积的前24位，所以进行24×24乘法时0~23位的计算直接舍去，24~42位进行非精确计算，43~47位进行精确计算，图5中实线框中进行非精确Booth编码及非精确压缩，虚线框进行精确Booth编码及精确压缩。
2.2 舍入单元
舍入单元的作用是在结果被返回放回浮点格式时，将多出来的位舍弃，使得有效数据的位数保持在固定的位数范围内。在精确浮点数乘法器中，IEEE列出了4种不同的舍入方法：舍入到最近(Round To Nearest，RTN)、朝正无穷大方向舍入(Round To Positive Infinity，RTPI)、朝负无穷大方向舍入(Round To Negative Infinity，RTNI)、朝0方向舍入(Round To Zero，RTZ)。在非精确设计中，乘积结果已是非精确的，舍入方法的选择对算法没有太大意义，所以在非精确浮点数乘法器中，舍入单元将不再考虑。
2.3 非精确浮点数乘法器结构
基于以上分析，非精确浮点数乘法器可以通过设计非精确无符号定点数乘法器、简化规格化处理及省略舍入单元来实现，具体结构如图6所示。
3 图像处理应用
很多非精确浮点数乘法都应用于图像处理中， OpenEXR是由Industrial Light and Magic开发的高动态范围图片(High Dynamic-Range，HDR)的文件格式，它支持16位及32位浮点。本文采用高动态范围图片来验证该非精确浮点数乘法器的有效性。高动态范围可视区分度检测(High Dynamic Range Visible Difference Predictor，HDR-VDP)是度量两幅图片区别的方法，它可以检测两幅图片的可视区别。图7、图8分别为精确、非精确浮点数乘法生成图片，两幅图片的区别检测图如图9所示。
HDR-VDP中整体可视检测中定义了两个度量方法，一个为P_det，定义为两幅图片的可视区别概率，它的范围为0~1，数值越大，说明两图片的区别人眼越容易察觉；另一度量方法是Q_MOS，它定义为图片的平均观测质量，它的范围是0~100，数值越大说明图片质量越好。经测量本文设计的非精确浮点数乘法器的两个度量值分别为：
度量值P_det表明两幅图片的差异不太容易被检测，度量值Q_MOS表明两幅图片质量很好。
4 结论
本文主要采用非精确定点尾数乘法器设计非精确浮点数乘法器，并将该乘法器运用到图像处理中，结果表明本文所设计的非精确浮点数乘法器具有很好的性能。
参考文献
[1] PALEM K，INGAMNENI A.Ten years of building broken-chips:the physics and engineeringofinexact computing[J].ACMTrans.Embedded Computing Systems，2013，12(2)，87：1-23.
[2] LINGAMNENI A，MUNTIMADUGU A，ENZ C，et al.Algorithmic methodologies for ultra-efficient inexact architectures for sustaining technology scaling[J].Proc.ACM Int.Conf.Computing Frontiers，2012：3-12.
[3] YANG Z，JAIN A，LIANG J，et al.Approximate XOR XNOR-based Adders for inexact computing[J].Proc.13rd IEEE Conf.Nanotechnol.(IEEE-NANO)，2013：690-693.
[4] Liu Weiqiang，Chen Linbin，Wang Chenghua，et al.Design and analysis of inexact floating-point adders[J].IEEE Transactions on Computers，2016，65(1)：308-314.
[5] Liu Weiqiang，Chen Linbin，WANG C，et al.Inexact Floating-Point Adder for Dynamic Image Processing[J].Proceedings of the 14th IEEEInternational Conference on Nano-technology Toronto，Canada，2014.
[6] TONG J Y，NAGLE D，RUTENBAR R.Reducing power byoptimizingthe necessary precision/rangeof floating-point arithmetic[J].IEEE Trans.Very Large Scale Integr.Syst.2000，8：273-286.
[7] GUPTA A，MANDAVALLI S，MOONEY V，et al.Low power probabilistic floatingpoint multiplier design[J].Proc.IEEE Comput.Soc.Annu.Symp.VLSI，2011：182-187.
[8] EILERT J，EHLIAR A，LIU D.Using low precision floating point numbers to reduce memory cost for MP3 decoding[J].Proc. 6th IEEE Workshop on Multimedia Signal Processing，2004：119-122.
[9] YEH W C，JEN C W.High-speed booth encoded parallel multiplier design[J].IEEE Trans.Computers，2000，49(7)：692-701.
[10] Amir Momeni，Jie Han，Paolo Montuschi，et al.Design and analysis of approximate compressor for multilication[J].IEEE Trans.Computers，2015，64(4)：984-994.
[11] MILLAR B，MADRID P E，SWARTZLANDER E E.A fast hybrid multiplier combining Booth and Wallace/Dadda algorithms[J].Proceedings of the 35th MidwestSymposium on Circuits and Systems，1992，1(8)：158-165.