刘斌，陈贤富，程政

　　（中国科学技术大学 信息科学技术学院，安徽 合肥 230027）

　　摘要：车载导航系统中最重要的功能是路径规划，传统车载导航设备大多采用静态算法，没有采用实时交通信息规划出的路径可能不是最优路径。结合一种动态行程时间表对传统A*算法进行调整，可以有效利用路网实时交通数据规避拥堵路线，从而实现动态路径规划。另外，实际应用中，单一的优化路径往往不能满足需求，对此提出重复路径惩罚因子的概念，构造出了一种多路径规划算法，可以在路径相似度与路径通行代价之间取得平衡，避免了传统Ｋ最短路径(K Shortest Paths, KSP)算法路径相似度过高的缺点。

　　关键词：动态路径规划；A*算法；动态行程时间表；重复路径惩罚因子；KSP

0引言

　　路径规划算法是智能交通系统(Intelligent Transportation Systems, ITS)的重要组成部分之一，尽管现实世界的实时交通信息在不断变化，但目前大部分车载导航系统采用的仍是静态的路径规划算法［1］，如A*算法［2］、Dijkstra算法［3］。此类算法假定道路通行代价不会改变，大多采用道路长度、宽度等静态属性作为路权计算方式，不能反映实时动态路况。

　　针对动态路径规划算法，参考文献［4］采用D* star算法对A*算法进行了改进；参考文献［5］针对道路的动态通行时间计算问题，提出了一种路网中道路动态通行时间表，表中记录了每个路段每个时间段的行程时间，由此得出了车辆经过路段的通行时间计算方法。

　　以上算法在点对点的路径规划中，只能得出单条优化路径，在实际应用中往往不能满足需求。对此存在许多一次可以求出多条优化路径的算法，称为KSP算法。参考文献［6］通过设置标号的办法得到K条最短路径；参考文献［7］提出了一种新的多标号算法来解决KSP问题。但上述KSP算法均存在路径相似度较高的缺点。参考文献［8-9］提出的算法可以求出一组边不相交链路，但各条路径相差较大。

　　本文通过分析上述算法的优缺点，结合A*算法与动态行程时间表，为减少接收行程时间表时的通信量，结合矩形限制搜索区域算法［10］，给出了一种求解单一优化路径的动态路径规划算法。同时提出一种重复路径惩罚因子，可以利用它一次搜索出多条优化路径，所求得的K条路径可以兼顾路径相似度与路径通行代价。

1A*算法

　　A*算法是一种典型的启发式搜索算法，建立在Dijkstra算法的基础之上，广泛应用于游戏地图、现实世界中，用来寻找两点之间的最短路径。A*算法最主要的是维护了一个启发式估价函数，如式(1)所示。

　　f(n)=g(n)+h(n)(1)

　　其中，f(n)是算法在搜索到每个节点时，其对应的启发函数。它由两部分组成，第一部分g(n)是起始节点到当前节点实际的通行代价，第二部分h(n)是当前节点到终点的通行代价的估计值。算法每次在扩展时，都选取f(n)值最小的那个节点作为最优路径上的下一个节点。

　　在实际应用中，若以最短路程为优化目标，h(n)常取作当前点到终点的欧几里得距离(Euclidean Distance)或曼哈顿距离(Manhattan Distance)等。若令h(n)=0，表示没有利用任何当前节点与终点的信息，A*算法就退化为非启发的Dijkstra算法，算法搜索空间随之变大，搜索时间变长。

　　A*算法步骤如下，算法维护两个集合：P表与Q表。P表存放那些已经搜索到、但还没加入最优路径树上的节点；Q表维护那些已加入最优路径树上的节点。

　　（1）P表、Q表置空，将起点S加入P表，其g值置0，父节点为空，路网中其他节点g值置为无穷大。

　　（2）若P表为空，则算法失败。否则选取P表中f值最小的那个节点，记为BT，将其加入Q表中。判断BT是否为终点T，若是，转到步骤（3）；否则根据路网拓扑属性和交通规则找到BT的每个邻接节点NT，进行下列步骤:

　　①计算NT的启发值

　　f(NT)=g(NT)+h(NT)(2)

　　g(NT)=g(BT)+cost(BT, NT)(3)

　　其中,cost(BT, NT)是BT到NT的通行代价。

　　②如果NT在P表中，且通过式(3)计算的g值比NT原先的g值小，则将NT的g值更新为式(3)结果，并将NT的父节点设为BT。

　　③如果NT在Q表中，且通过式(3)计算的g值比NT原先的g值小，则将NT的g值更新为式(3)结果，将NT的父节点设为BT，并将NT移出到P表中。

　　④若NT既不在P表，也不在Q表中，则将NT的父节点设为BT，并将NT移到P表中。

　　⑤转到步骤（2）继续执行。

　　（3）从终点T回溯，依次找到父节点，并加入优化路径中，直到起点S，即可得出优化路径。

2动态行程时间表及A*算法调整

　　2.1动态行程时间表

　　为计算在实时情况下某段道路的通行时间，采用了一种道路通行时间表的结构，表中存放了道路当前时刻的通行时间以及未来几个时刻通行时间的预测值。

　　以t0表示导航系统开始工作的时刻，将未来一段时间划分为若干个时段，以ΔT表示一个时段的长度，系统开始工作的时刻属于第一个时段。然后对这些时段进行编号，如1,2,3,4，…。同理，也将每条道路编号为1,2,3,4，…。采用Tij表示路段i在时段j的通行时间。这样就可得到不同道路在不同时刻的通行时间，将它们记录为表1。 

　　车载系统可能会在某个时刻进行路径规划，优化路径上可能会包含多个路段，将它们编号为1,2,3,…，k,…。以［tk,tk′］表示车辆经过路段k的通行时间Tk,则Tk= tk′-tk。车辆可能会花费多个时段才能通过路段k，将这些时段与通行时间Tk1′,Tk2′,Tk3′,…对应。

　　首先计算出车辆经过路段k起点的时刻对应的时段fk:

　　其中，」符号表示对结果取下整。则相应地可得出：

　　T′ki=Tk(fk+i-1)(5)

　　根据时段长度ΔT、道路长度L与道路通行速度的不同取值，可能会出现车辆只需在一个时段即可通过路段，也可能需要多个时段才能通过。因此经过牛顿运动学原理进行计算，可得到车辆通过路段k的具体公式如下［9］：

　　其中，m的取值满足：

　　2.2A*算法调整

　　在得出车辆通过路段k的计算方法后，即可对传统A*算法进行调整，以搜索出动态优化路径。具体如下：

　　在A*算法描述的第（2）步中，首先计算出起点S到达BT的通行时间t，则到达BT的时刻为出发时刻加上t，记为tBT，然后根据式(6)计算出BT到达NT的通行时间T。则可更新g(NT)为：

　　g(NT)=g(BT)+T+tli(8)

　　其中，tli表示路口红绿灯等待时间。除了这些调整外，前述A*算法的其他部分不需要改变。

3动态多路径规划算法

　　3.1算法描述

　　上述调整后的A*算法一次只能搜索出单条动态优化路径，为了在给定起点S与终点T之后得到多条在通行代价与路径相似度之间取得平衡的动态优化路径，提出了一种重复路径惩罚因子的概念。算法的总体思想是：首先利用上述调整后的A*算法搜索出一条优化路径后，将此优化路径上每条道路的通行代价都乘以惩罚因子，然后再利用算法搜寻下一条优化路径。在描述算法之前，首先需要定义几个符号：Pk为S到T之间的第k条优化路径；Lk为Pk的长度；PC为存放优化路径的集合；OLnk为第n条优化路径与第k条优化路径的重合度，表示为两条路径上重复路段的总长度, k=n-1,n-2,…，1；Dnk为第n条优化路径与第k条优化路径的相似度，Dnk=OLnk/Ln,k=n-1,n-2,…，1；MO为设定的最大相似度；PO为重复路径惩罚因子，PO=(1MO)β,β为一个正系数；K为希望搜索出的最大优化路径条数；n为当前已规划出优化路径条数。

　　利用这些符号，算法可描述如下：

　　（1）设置MO、β和K，令n=0;

　　（2）利用调整后的A*算法搜索出一条优化路径,将其加入PC中，n=1;

　　（3）若n大于等于K，算法结束，否则将Pn上每一条路段的通行代价都乘以PO;

　　（4）路径规划与相似度计算：

　　①n=n+1;

　　② 利用改造A*算法规划出下一条优化路径Pn;

　　③ 计算相似度：

　　Dnk=OLnk/Ln，k=n-1,n-2,…，1

　　④路径相似度判断：

　　若Dnk>MO，算法结束，否则将Pn加入 PC，转步骤（3）。

　　利用此算法最多可以求出K条优化路径，各条优化路径的通行代价与相似度取决于MO与β的取值。当MO=1.0时，相当于没有惩罚，此时只能得出一条路径；当MO<1.0时,可以得到多条路径。

　　3.2实验结果

　　图1本文算法规划结果本文采用真实的合肥城区电子地图数据，构建了一个C/S(Client/Server)模型，由服务器端模拟产生实时交通数据，每条道路的通行时间范围为道路畅通时的时间到7倍于它之间的一个随机值。在车载终端请求实时数据时，终端会发送起点、终点坐标值给服务器，服务器采用矩形限制搜索区域算法,大大减少了通信的数据量。

　　以从“中国科学技术大学第一教学楼”到“安徽大学新校区”为例，规划结果如图1所示。 其中的参数设置为：MO=0.5，β=1.8，K =3。优化3条路径。路径长度与相似度统计如表2所示。

　　表2优化路径通行代价与相似度路径123长度/km13.4315.9216.37最大相似度/%-13.6330.78其中最大相似度表示的是此道路与标号小于它的那些道路的最大D值。作为对比，百度地图的搜索结果如图2所示。　

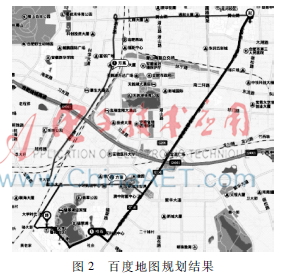
　　3条道路的长度分别为14.3 km、16.4 km与19.1 km。

4结论

　　在本文中，提出了一种基于传统A*搜索算法，并结合动态通行时间表、矩形限制搜索区域算法与道路相似度惩罚因子的多优化路径规划算法。实验结果显示，在给定起点和终点的情况下，本文提出的算法能有效规划出在通行代价与路径相似度之间取得平衡的多条路径，有效解决了传统KSP算法路径相似度过高的缺点，同时提高了算法的实时性。

　　参考文献

　　［1］ NADI S, DELAVAR M R. Locationbased service for Invehicle route guidance with real time traffic information［C］.The 12th World Conference on Transport Research (WSTR to WCTR) Proceedings, 2010: 110.

　　［2］ GOLDBERG A V, KAPLAN H, WERNECK R F. Reach for A*: efficient pointtopoint shortest path algorithms［C］.ALENEX, 2006, 6(2): 129143.

　　［3］ MHRING R H, SCHILLING H, SCHTZ B, et al. Partitioning graphs to speed up Dijkstra’s algorithm［M］.Experimental and Efficient Algorithms. Springer Berlin Heidelberg, 2005,11(28): 189202.

　　［4］ 随裕猛, 陈贤富, 刘斌. Dstar Lite 算法及其动态路径规划实验研究［J］. 微型机与应用, 2015, 34(7): 1619.

　　［5］ 苏永云, 晏克非. 车辆导航系统的动态最优路径搜索方法研究［J］. 系统工程, 2000, 18(4): 3237.

　　［6］ DREYFUS S E. An appraisal of some shortestpath algorithms［J］. Operations research, 1969, 17(3): 395412.