俞霖炜，曾培峰

　　(东华大学 计算机科学与技术学院，上海 201620)

　　摘要：讨论了实际工业生产中点状缺陷的实时检测问题，提出一种基于嵌入式的一维缺陷检测方法。首先通过行灰度信息的变化定位缺陷位置，并针对缺陷处于特定位置、图像有噪声、光照不足或过度等特殊情况提出了改进方案，实现了点状缺陷的实时监测。实验结果证明，该算法具有准确性和有效性。

　　关键词：工业生产；点状缺陷；一维检测；实时检测

0引言

　　近年来，缺陷检测一直是一个热门的研究方向，广泛运用在工业生产缺陷检测中。为了在工业生产中实现嵌入式控制的实时缺陷检测，本文提出了一种基于嵌入式的一维缺陷检测方法，先通过行灰度信息的变化快速定位缺陷位置，再针对缺陷处于特定位置、图像有噪声、光照不足或过度等特殊情况提出了改进方案，实现了点状缺陷的实时监测。此外，本文还讨论了在摄像头倾斜情况下，计算缺陷实际位置的矫正算法。

1研究现状

　　现有的缺陷检测算法大致可以分成五大类：统计学法、结构化法、光谱法、基于模型的方法以及机器学习的方法。

　　统计学法根据像素间的空间分布关系检测缺陷，自相关函数［1］、灰度共生矩阵［2］等都是经典的统计学方法。自相关函数易于处理具有强正则性的纹理图像，但是它易受噪声影响，不太适合处理纹理不规则的图像。灰度共生矩阵对单调灰度变换具有不变性［2］，它的空间表现优于自相关函数。然而，当纹理图像清晰度高或是存在大量邻接像素需要高强度计算时，灰度共生矩阵的性能表现不佳。

　　结构化法将纹理描述成由许多纹理基元组成的集合，这些基元可以是单一像素也可以是一块区域，通过这些基元的布局规则，就能找到无序缺陷所在的位置［3］。

　　光谱法主要有傅里叶变换、加伯变换、小波变换以及图像滤波等。傅里叶变换需要通过整张图像来提取信号，不能有效地定位缺陷区域，通常会采用加窗傅里叶变换来解决这一问题。当窗函数是高斯函数时，加窗傅里叶变换就变成了加伯变换［46］。

　　最著名的基于模型的方法是自回归模型以及马尔可夫随机场模型。自回归模型［78］通过捕捉纹理图像上不同的像素描述线性关系，这种方法易于识别微小的缺陷，且不易受到图像平移的影响，但它受光照的影响较大。马尔可夫随机场模型认为图像中像素的强度取决于其相邻几个像素的像素强度。在执行时间上，马尔可夫随机场模型大大优于其他的随机场模型［9］，但它不容易识别微小的缺陷。

　　最近，也有一些机器学习的方法运用在缺陷检测上。参考文献［1012］都拥有高于90%的缺陷检测率。但是机器学习的方法在特征数据不充分时，往往得不到满意的效果。

2一维行扫描法

　　一维行扫描的方法通过行灰度信息的变化快速定位缺陷位置。

　　2.1算法的基本原理

　　针对缺陷灰度值局部最小的特点，对于每一行数据，可以通过如下定义来识别缺陷：

　　定义1x∈［0,m－1］,若α>0,使得h1(t)<min(|Pn(x－α)－Pn(x)|,|Pn(x+α)－Pn(x)|)<h2(t)，则x∈Xdefect

　　其中，变量m、n分别表示图像Im×n的宽和高。函数Pn(μ)是图像中第n行第μ列的像素灰度值，μ∈［0,m－1］。函数h1(t)、h2(t)是光强度t下的上下波幅阈值，它们决定了缺陷与背景灰度之差的浮动范围。

　　为了提高计算速度，可以事先求得明背景的平均阈值Thl和暗背景的平均阈值Thd，仅对0<Pn(x)<Thd－h1(t)以及Thl－h2(t)<Pn(x)<Thl－h1(t)的像素进行处理。除非光照发生变化，Thl和Thd在一次实验中只需要计算一次。为了更进一步提高计算速度，对于每一行的数据，可以首先计算它们的像素和作为校验和，式(1)为校验和Sn的计算公式：

　　当|Sn－Sn′|>β，则认为第n行存在缺陷。其中：Sn′是上一帧图像中第n行像素灰度值的校验和，β是根据缺陷的形状和大小信息预先设定的经验值。因此，仅对存在缺陷的行数据做进一步的计算，可以大大减小计算量。

　　在大多数情况下，通过定义1就能够获得很好的结果，但在当缺陷位于明暗背景的边界处、图像噪声的最大方差较大、光照不足或过度时，图像处理的效果将欠佳。特别是当图像在采取过程中产生偏移时，式(1)将会失效。针对这些特殊情况，将进一步给出相应的改进方案。

　　2.2边界问题

　　图像的明背景与暗背景之间通常会产生分明的边界，反映在直方图上会产生明显的幅值变化。缺陷位于边界处可分为三种情况：(1)缺陷整体处于明背景部分；(2)缺陷整体处于暗背景部分；(3)缺陷处于明暗背景之间。这三种情况都容易造成漏判，图1分别给出了这三种情况。

　　对于上述情况，定义2给出了新的判断检验和方法，Tn表示图像中第n行像素灰度值的检验和，它不再对整行的数据求和，只对梯度发生较大变化的数据求和。

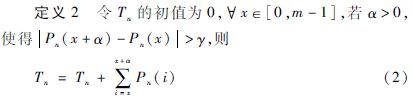
　　其中，γ是一个经验值，γ的大小根据明暗背景的幅度来决定，本文选取γ=18(Thl－Thd）。采用新的校验和有以下优点：

　　(1)仍然能够作为校验和判断缺陷的产生。

　　(2)不仅能够检验边界处的缺陷，还能够判断缺陷究竟是位于边界部分，还是位于背景部分。Tn′是上一帧图像中第n行像素灰度值的新校验和，当|Tn－Tn′|>β时，表示第n行存在缺陷。当Tn<Tn′时，则表明缺陷处于边界部分；当Tn>Tn′时，则表明缺陷处于背景部分。

　　(3)能够忽略采集过程中图像的轻微偏移。通常，如果在当前行的位置x处发生梯度变化，相邻行也将会在x的邻域处发生梯度变化，因为新的校验和只对梯度发生较大变化的像素值求和，且行间的像素变化是连续的，所以图像的轻微偏移不会导致新的检验和失效。

　　2.3图像噪声问题

　　如果图像噪声的幅值较大，将会把某些噪声误判为缺陷。针对这种情况，可以引入一个阈值Thc来判断每一行中每一个缺陷所占像素的范围。实现方法如下：在扫描中每当发现疑似缺陷，通过缺陷的起始坐标Xb、终点坐标Xe求得缺陷的像素范围count=Xe－Xb+1。当count>Thc时，将疑似缺陷判定为真正的缺陷，否则将其判定为图像噪声。当识别完一个疑似缺陷后，count清零，继续判断之后发现的疑似缺陷。Thc的大小与噪声的类型以及图像的清晰度有关。

　　上述方法对零散的高幅值噪声过滤效果较好，但是会疏漏连续出现的噪声，因此可以引入行间检查的方法。具体步骤如下：(1)记录图像中每一行内缺陷区域的个数，这样，一幅m×n大小的图像就会形成一个大小为n的一维数组F［n］；(2)将F［n］通过式(3)转化为另一个数组G［n］，就能判断是否有噪声被误判成缺陷。

　　由于每个缺陷都有一定的面积，行间的数据变化也是有规律的，G［n］上的数据不会发生剧烈变化。但当有噪声出现时，G［n］上的数据将变化得非常明显。因此，根据这种方法就能判断是否存在噪声误判。实际应用中，如果一定范围内G［i］的值都大于0，就认为该区域有噪声误判。当确定了误判，就能通过重新扫描这些行快速过滤误判噪声。

　　2.4光照问题

　　光照不足或是光照过度都会影响采集图像的质量，本文通过自动调节相机增益来稳定光照。实际应用中的流程图如图2所示，先计算直方图中一个波峰的横坐标值Th2，通过自动调节相机增益使得Th2满足a<Th2<b，其中a、b都是预先给定的经验值，这两个参数保证采集到的图像光照最佳。通过固定时间重复这个过程就能达到稳定光照的目的。由于该方法仅采用Th2作为光照强度的判断依据，对于直方图并不是双峰的情况也依然适用。

3梯形失真消除

　　梯形失真的图像是由真实图像经过仿射变换转换而成的，由于仿射变换保持同素性，梯形失真的图像经过仿射变换也能转换成真实图像。对于任意坐标(x,y)经过仿射变换转换得到坐标(u,v)，都有如下关系：

　　u=Ax2+By2+Cxy+D

　　v=Ex2+Fy2+Gxy+H(4)

　　其中，A、B、C、D、E、F、G、H是8个变换参数。

　　因此，只需要知道变换前与变换后4个坐标的坐标值，代入式（4）即可求得8个变换参数，也就得到了失真图像与真实图像之间的转换关系。

4实验结果分析

　　本文采用一维行扫描法对点状缺陷进行检测，图3给出了该算法在实际应用中的检测效果。

　　为了验证算法的效率，本文对相同时间内不同算法在嵌入式设备中能够处理的帧数进行了比较试验。图4是两种一维缺陷检测方法（一维加伯变换法和一维自相关函数法）、常规的二维缺陷检测方法和本文算法的比较。结果表明，本文的算法在效率上优于常规的二维缺陷检测方法以及加伯变换法和一维自相关函数法缺陷检测方法。

5结论

　　本文提出了一种基于嵌入式的一维缺陷检测方法，并针对特殊情况，给出了算法的改进方案。实验结果证明，该算法拥有良好的缺隐检出率，并且在算法效率上略优于其他同类型算法。

参考文献

　　［1］ HARALICK R M.Statistical and structural approaches to texture［J］.Proceedings of the IEEE,1979,67 (5):786804.

　　［2］ MOKJI M M,BAKAR S.Adaptive thresholding basedon cooccurrence matrix edge information［C］. First Asia International Conference on Modelling& Simulation, IEEE, 2007:444450.

　　［3］ VILNROTTER F, NEVATIA R, PRICE K. Structural analysis of natural textures［J］. Pattern Analysis and Machine Intelligence, 1986,8(1):7689.

　　［4］ CLARK M, BOVIK A C, GEISLER W S. Texture segmentation using gabor modulation/demodulation［J］.Pattern Recognition Letters, 1987, 6(4):261267.

　　［5］ VALOIS R L D, ALBRECHT D G, THORELL L. Spatial frequency selectivity of cells in macaque visual cortex［J］. Vision Research, 1982, 22(5):545559.

　　［6］ JAIN A K, FARROKHNIA F. Unsupervised texture segmentation using gabor filters［J］. Pattern Recognition, 1991, 24(12):11671186.

　　［7］ SERAFIM A F.Multiresolution pyramids for segmentation of natural images based on autoregressive models: application to calf leather classification［C］. 1991 International Conference on Industrial Electronics, Control and Instrumentation, IECON′91, IEEE, 1991: 18421847.

　　［8］ HAJIMOWLANS S H, MUSCEDERE R, JULLIEN G A,et al. 1D auto regressive modeling for defect detection in web inspection systems［C］. Proceedings of Midwest Symposium on Circuits and Systems,1998,1:330333.