李涛

　　(四川大学 计算机学院，四川 成都 610065)

       摘要：传统Retinex算法中，从图像中完全去除亮度分量而使用反射分量来增强效果。通常图像光照变化并非平缓，使得结果图像视觉效果缺乏协调。对此提出一种改进的Retinex算法，通过再处理亮度分量，得到平缓的亮度图像并补偿到反射分量从而改善增强效果，使用均值模版代替高斯模版以减少计算的时间，同时利用拉普拉斯算子加入图像边缘细节特征。实验通过处理低对比度、低亮度的X光射线将改进的Retinex方法与其他各种增强算法进行对比。对实验结果的定性和定量分析表明了该改进算法的有效性。

　　关键词：多尺度Retinex；均值模版；平滑光照；拉普拉斯算子

0引言

　　图像增强是图像分析、图像分割等其他图像处理的预处理，其目标是满足人眼的需要有选择性地强调或者抑制图像中的某些信息［1］。目前，有许多的增强方法经常出现在各个应用中，例如伽马校正、直方图均衡化和小波变换等［2］，对图像增强的发展起到了一定的引导作用，但各自表现出明显的不足。1977年，LAND E H根据人类视觉中对光照和色彩感知提出了Retinex模型［3］。Retinex理论就是去除图像中亮度信息而保留反射信息来恢复物体的原始信息，从而达到增强效果。然而，当图像中光照分布不均匀或者光照不是平缓变化时，仅仅通过滤波器得到的反射分量不能完全满足要求。

　　针对Retinex算法存在的一些不足，通过对亮度分量进行滤波处理以补偿增强后的图像；算法过程中存在大量的卷积操作，大大降低了算法运算效率，根据大尺度高斯模版的均值特性，使用均值模版代替高斯模版对图像进行滤波操作；最后通过拉普拉斯算子增加图像的细节信息。

1Retine增强算法理论

　　根据Retinex理论将图像视为物体亮度分量L(x,y)和反射分量R(x,y)，则真实图像函数I(x,y)表达式为：

　　I(x,y)=R(x,y)*L(x,y)(1)

　　LAND E H在此基础上扩展提出中心/环绕Retinex算法［4］（即局部Retinex），JOBSON D J［5］等人在中心/环绕Retinex的基础上，提出了单尺度的Retinex算法，该算法的数学公式为：

　　R(x,y)=logI(x,y)－log［I(x,y)*F(x,y)］(2)

　　其中，R(x,y)表示输出的图像；*为卷积运算；F(x,y)表示中心/环绕函数，一般采用高斯函数，可以达到很好的增强效果。环绕函数F(x,y)表达式为：

　　其中，标准差σ即为尺度参数。当σ取值较小时，能够很好地实现动态范围压缩，图像局部信息较为突出，偏暗区域的边缘细节能够得到较好的增强，但是会出现颜色失真现象；当σ取值较大时，图像整体和颜色保真效果较好，图1肋骨图像高斯模版和均值模版滤波比较图但是动态压缩能力与细节增强效果较差。K是归一化因子，使得：

　　F(x,y)dxdy=1(4)

　　由式（4）可以看出，单尺度Retinex算法的增强效果主要依赖于高斯函数标准差σ的选取，单一的σ取值难以同时实现动态范围压缩、局部信息突出和较好的颜色保真效果。在此基础上JOBSON D J进一步提出了多尺度Retinex算法。

　　多尺度Retinex算法就是通过不同尺度的环绕函数对图像进行处理，可以看作多个不同尺度的单尺度Retinex线性加权求和，其表达式为：

　　其中，k表示环绕函数的个数，Wi表示不同尺度环绕函数的加权系数。在实际环境中，环绕函数的标准差一般选取大中小3个尺度，而权值Wi可以根据实际需求侧重点的不同而选取，在通常情况下，每个权值都选择相同的1/3比较合适。多尺度Retinex算法一定程度上兼顾了图像的整体效果和局部突出，又保证了动态范围压缩和色彩的一致性。

2多尺度Retinex算法的改进

　　2.1利用均值模版代替高斯模版

　　由式(5)可以看出，多尺度Retinex算法需要计算每个尺度的高斯模版与原始图像的卷积，而对于尺度较大的模版做卷积运算的计算量非常大，这大大地影响了算法的效率。

　　当高斯模版的尺度选取较大时，其高斯模版加权矩阵中的权值非常小，并且数值大小均很接近［6］。对于尺度大小为129×129的高斯模版，其权值的变化范围为0.561 4×10－4~0.621 9×10－4，从数值上可以看出，权值最大值与最小值之间的差异仅为0.605×10－5，因此如果将高斯模版中这些变化差异不大的权值使用固定值代替，会使得卷积运算变得简化。高斯模版中权值相加的和近似为1，采用均值模版的思想，将权重平均分配到每一个数值上［7］。针对上面的129×129模版，计算1/1292，得到的结果近似为0.600 9×10－4，选用这个数值代替高斯模版中的数值，将高斯模版权值转换为固定值进行计算。

　　选择低亮度、低对比度的肋骨图像分别使用高斯模版和均值模版进行处理。肋骨图像的大小为100 4×100 4。如图1所示，当模版选用129×129时，从主观上看两种滤波后的效果几乎没有差异，而当模版选用33×33时，两种滤波效果差异也并不大，因此可以采用均值模版代替大尺度的高斯模版。

　　2.2保留部分亮度分量补偿目标图像

　　在引言中提到过，传统的Retinex算法将过滤得到的亮度分量从原始图像中完全移除。由式(1)的等价公式得到：

　　R(x,y)=logL(x,y)R(x,y)L(x,y)R(x,y)≈logR(x,y)R(x,y)(6)

　　式（6）中，（x,y）为环绕加权平均值，即Retinex实际是当前点亮度与四周环绕加权平均亮度的比值，符合人眼视觉感知的神经生理学机制［8］。若当前点亮度与四周环绕光照强度基本相同，或光照变换缓慢，即公式约等号成立。然而更多情况下图像并不满足约等号成立的条件，对于光照变换不平缓的区域不能完全消除光照的影响［9］。

　　低频部分L(x,y)代表着灰度级变化缓慢的区域，因此，可以过滤由原始图像得到的亮度分量［10］,保留原始图像中部分的亮度信息。在Retinex算法中，亮度图像由低通滤波得到，其公式为：

　　L(x,y)=I(x,y)*F1(x,y)(7)

　　F1(x,y)为第一次过滤的环绕函数，L(x,y)就是原始图像中的亮度信息。由于亮度不均匀，因此L(x,y)中灰度变化仍然是动态的，而这些灰度动态变化的区域正好就是原始图像中亮度不均匀的区域。于是再次过滤L(x,y)，其公式为：

　　L1(x,y)=L(x,y)*F2(x,y)(8)

　　F2(x,y)为二次过滤的环绕函数。对于F1(x,y)和F2(x,y)的滤波模版，本文选用上一节介绍的均值模版。可以通过调整模版大小，消除L(x,y)中高频的部分，从而得到相对均衡的亮度L1(x,y)，对图像亮度补偿达到良好的视觉效果。

　　图2(a)是lena图像过滤得到的亮度部分，可以看出来它是不均匀的，而图2(b)经过两次过滤后得到的L1(x,y)，很明显相对于图2(a)在亮度更加平缓。这表明通过二次过滤能够修正亮度不均匀区域，进而得到相对均衡的亮度。　

　　2.3图像边缘细节增强

　　为每一个像素进行同比增强，则增强后的图像的边界和轮廓会比较模糊，因为这种增强方式减小了相邻像素点之间的灰度差异。而人类视觉系统有增强边缘对比度的机制［11］，当人眼观察图像中两块亮度不同的区域时，若边缘处对比度增高，会产生强烈的对比和反差，使得图像轮廓更加清晰。拉普拉斯算子可以保留像素之间的灰度差异，增强灰度突变处的对比度，在保留图像背景的前提下突显图像的边缘细节信息。为了更适合于数字图像处理，使用离散的拉普拉斯算子的模版形式。图3所示为两种常见的拉普拉斯模版。图像的边缘就是那些灰度发生跳变的区域，所以拉普拉斯模版有利于突出这些边缘细节信息。

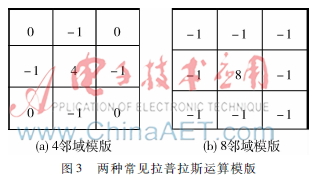
　　实验中笔者采用4邻域拉普拉斯运算模版。将拉普拉斯模版与原始图像做卷积运算，再用原图像减去卷积结果得到图像边缘影像，其公式如下：

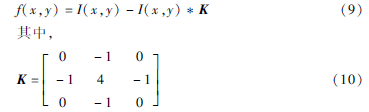
3改进的MSR算法描述与实验

　　3.1改进的MSR算法描述

　　根据Retinex理论［12］，通过分析与改进，本文的算法可以大致分为以下步骤：

　　（1)根据图像选取适当的均值模版进行滤波处理，分别得到亮度分量L(x,y)、反射分量R(x,y)。

　　（2)对L(x,y)再次进行过滤操作，得到均衡的亮度L1(x,y)，补偿R(x,y)得到增强图像R1(x,y)。

　　（3)通过式(9)用拉普拉斯模版对原始图像进行处理，得到图像边缘细节信息。

　　（4)将增强后的图像与边缘图像叠加，并拉伸修正到显示器正常显示范围，得到最终的增强图像。

　　3.2实验结果及分析

　　实验对X射线脊柱和颈椎图像［13］进行增强处理，图像大小为1 004×1 004，分别采用伽马校正、MSR算法以及本文改进的算法进行处理比较。

　　图4为不同算法的增强效果对比。从图4可以看出，不同的增强方法都使得图像视觉效果得到改善［14］。伽马校正［15］一定程度上增强了图像的对比度和亮度，但增强的图像整体较暗且模糊，视觉效果依然很差；MSR增强算法提高了图像的亮度、对比度，但图像的边缘信息较差，同时层次感有所降低；本文的算法有效地解决了MSR算法的缺点，保留了图像的边缘信息，能够清晰显示出骨骼的轮廓。

　　图4从主观的角度对比分析了几种增强算法的优劣，下面通过计算图像的信息熵［16］，定性地分析比较处理后的效果，如表1、表2所示。

　　从表1中可以看出，MSR算法和本文算法处理后图像信息熵得到了提高，而本文算法提高得更多。本文采用均值模版代替高斯模版，减少了MSR算法中大量的卷积运算，从表2看出在运算时间上有一定程度的提升，且图像越大，提升越明显。虽然文章加入拉普拉斯算子增加图像边缘信息消耗了一定的时间，但从信息熵和运行时间来看，本文算法对MSR算法的改进都有着明显的效果。

4结论

　　通过多尺度Retinex算法的分析以及实现，发现MSR算法存在着灰度级不均匀，细节特征模糊等不足，于是通过平缓亮度图像补偿反射分量，再运用拉普拉斯算子增加图像边缘对增强效果进行改善。实验结果较好地说明了改进的算法能够对亮度较差且光照不均匀、对比度不高的图像进行有效的增强，增强后的图像亮度和对比度明显提高，图像细节信息得到提升，图像边缘更加清晰，更加符合人眼视觉效果。

参考文献

　　［1］ 陈炳权，刘宏立，孟凡斌.数字图像处理技术的现状及发展方向［J］.吉首大学学报(自然科学版)，2009,30(1):6370.

　　［2］ 赵晓霞，王汝琳.改进的多尺度Retinex算法及其应用［J］.计算机工程，2011,37(6):209211.

　　［3］ LAND E H.The Retinex theory of color vision［J］.Scientific American,1977,237(6):108128.

　　［4］ LAND E H.An alternative technique for the computation of the designator in the Retinex theory of color vision［J］.Proceedings of the National Acaclemy of Sciences,1986,83(10):30783080.

　　［5］ JOBSON D J,RAGMAN Z,WOODELL G A. Properties and performance of a center/surround Retinex［J］.IEEE Transactions on Image Processing,1997,6(3):451462.

　　［6］ 王科俊，熊新炎，任桢,等.基于窗口无关均值滤波的MSR图像增强［J］.哈尔滨工业大学学报，2010,42(9):14671471.

　　［7］ 陈琛，张建州.改进的多尺度Retinex医学X射线图像增强算法［J］.计算机工程与应用，2015,51(9):191-195.

　　［8］ 曾强，何士刚.视网膜中的自主感光神经节细胞［J］.生物物理学报，2011(5)：387394.

　　［9］ 唐亮，谢维信，黄建军,等.城市航空影像中基于模糊Retinex的阴影消除［J］.电子学报,2005,33(3):500503.

　　［10］ Wang Wen, Li Bo, Zhang Jin, et al. A fast multiscale Retinex algorithm for color image enhancement［C］. Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition, Hong Kong: IEEE,2008:3031.

　　［11］ RAHMAN Z U, JOBSON D J, WOODELL G A. Investigating the relationship between image enhancement and image compression in the context of the multiscale retinex［J］. Journal of Visual Communication & Image Representation,2011,22(3):237250.

　　［12］ 王彦臣，李树杰，黄廉卿.基于多尺度Retinex的数字图像X光图像增强方法研究［J］.光学精密工程,2006,14(1):7076.

　　［13］MOREL J M, PETRO A B, SBERT C. A PDE formalization of retinex theory［J］. IEEE Transctions on Image Processing,2010,19(11):28252836.

　　［14］ 李锦，王俊平，万国挺,等.一种结合直方图均衡化和MSRCR的图像增强新算法［J］.西安电子科技大学学报(自然科学版)，2014,41(3):103109.

　　［15］ 彭国福，林正浩.图像处理中Gamma校正的研究和实现［J］.电子工程师，2006,32(2)：3032.

　　［16］ 吴成茂.一种新信息熵定义及其在图像分割中的应用［J］.西安邮电学院学报，2009,14(1):7279.