吴晶，徐名海，顾宏博，奚杰杰

　　(南京邮电大学 通信与信息工程学院，江苏 南京210003)

　　摘要：针对现有交通分配研究对驾驶员有限理性、道路交通动态随机性的忽视，提出一种基于智能代理的动态交通分配模型IATAM，其以驾驶员为代理，依据驾驶员的路线偏好，综合驾驶员信息处理的模糊随机过程，考虑邻居驾驶员影响，提出神经网络结构的驾驶员智能路线决策机制。实验中IATAM模型检测点车流量与真实车流量的平均相对误差减小到6.42%，表明IATAM模型实验精度更高，更符合复杂多变的交通环境。基于智能代理进行交通分配，更能反映驾驶员的异构性和路线决策的模糊随机性，并有效提高交通分配精度。

　　关键词：智能交通；交通分配；智能代理；驾驶员行为；路线决策

0引言

　　交通分配中路网的实际状况、各路段车流量、驾驶员路径选择行为等，是分析交通状况、评价现状路网、确定路网规划、预测交通控制效果、进行交通诱导等的主要依据。为了更好规划路网，有效分析、控制和诱导交通流，需要构建真实合理的交通分配模型。

　　传统的交通分配方法主要有宏观交通分配［12］和微观交通分配，其中，微观交通分配从驾驶员个体出发挖掘交通流内在特性，能更真实体现驾驶员的路线决策行为。现有文献基于驾驶员路线决策分析展开了不少研究，形成了不同路线选择类型［3］、影响因素［4］、环境改变［5］下的交通分配模型，但对驾驶员的有限理性以及道路交通条件的动态随机性等研究还比较有限。

　　本文提出基于智能代理的动态交通分配模型(Traffic Assignment Model Based on Intelligent Agent ,IATAM)。IATAM模型以不同偏好的驾驶员为代理，通过对模糊逻辑和随机阻抗的路线选择行为的分析，融合驾驶员间的相互影响，考虑路线决策随环境的动态变化，提出了驾驶员的智能路线决策。这种建模方法体现了路网交通的时变性和驾驶员代理的异构性、自治性和主动性，并考虑了交通问题的模糊性和随机性，更符合实际路网。

　　本文详细介绍了驾驶员智能路线决策模型，给出了基于智能代理的动态交通分配模型，并对模型进行了实验和验证。

1驾驶员智能路线决策模型

　　交通分配需要把OD矩阵所对应的交通量分配至路网，决定所有车辆的行驶路线，交通分配的结果是所有起讫点间驾驶员路线决策行为的整体汇聚。本文采用微观方法，通过对驾驶员路线决策行为建模，并采用基于代理的实验方法，尝试解决交通分配问题。

　　1.1应用场景及技术需求

　　图1是驾驶员m、n和k从A点去往F点的决策路线，由图分析3位驾驶员的路线决策行为。

　　图2驾驶员智能路线决策模型A点到F点某一时间段的交通出行为50辆/min，各路段长度和平均行驶时间如图1所示。驾驶员m的路线偏好是最短路径，只考虑各路段长度，ABF的感知长度大约为1 400 m，驾驶员认为ABF是最优路线，由于其拥塞避免指数很低，即使感觉周围车流密度较大，也不会更改行驶路线。驾驶员n的路线偏好也为最短路径，准备沿ABF行驶，但其拥塞避免指数很高，综合本路段和下一路段的拥挤情况，决定避开拥挤选择车流量相对较少的路径ABEF，此时路线偏好受周围环境的影响变为时间最短。驾驶员k的路线偏好为时间最短，选择ADEF，其拥塞避免指数虽然较高，但由于道路通畅，并不改变行驶路线。

　　上述情景，不同驾驶员的路线决策行为不同。对驾驶员路线决策行为建模需要考虑以下技术需求：

　　（1）驾驶员建模应考虑驾驶员的异构行；

　　（2）驾驶员路线决策应考虑驾驶员主观信息的模糊性和信息处理的非完全理性；

　　（3）驾驶员路线行驶中应考虑交通环境因素的动态随机性和驾驶员之间的相互影响。

　　1.2驾驶员智能路线决策算法

　　根据上述应用场景和技术需求描述，本文以驾驶员为代理，考察驾驶员的路线决策行为。

　　驾驶员路线决策时，会对个人信息和环境信息同时进行处理，协调完成路线的决策，且经历信息接收、分析、判断和决策，输出的行为又会对下一时刻的环境和个人思维产生影响。由于驾驶员路线决策的分布式并行信息处理、层次关系、反馈机制和人工神经网络［6］信息处理过程类似，本文采用神经网络结构描述路线决策机制；又因为驾驶员主观信息的模糊性和路网客观信息的随机性，本文采用模糊逻辑［7］和随机变量描述路线决策的相关变量。驾驶员智能路线决策模型如图2所示，驾驶员对信息的处理经过了输入层、感知层、决策层和输出层，驾驶员行为和主观思维又对下一时刻产生影响。

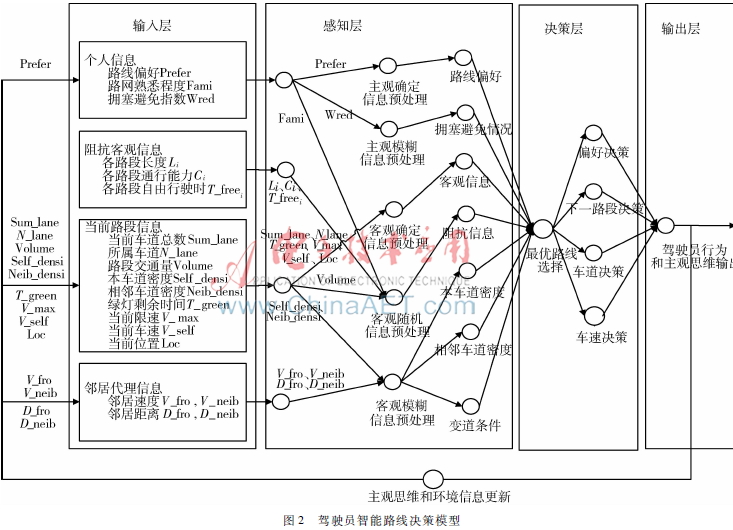
　　输入层主要包括个人信息和环境信息。感知层是驾驶员对输入信息的提取过程，驾驶员在对输入信息分类整理后进行预处理。决策层是驾驶员对感知信息处理后进行的路线决策，决定下一时刻的路线偏好、行驶路段、车道和车速。输出层是驾驶员依照决策层进行的行为表现和主观思维改变。

　　对于输入层，本文将驾驶员路线决策过程需要的信息分为4类：个人信息、阻抗信息、当前路段信息和邻居代理信息。个人信息即驾驶员本身的特性。阻抗信息即驾驶员对路网阻抗的整体了解。当前路段信息即驾驶员此刻所处路段客观信息。邻居代理信息即驾驶员邻居车辆信息。各类信息所包含的具体内容以及对应变量如表1所示。 

　　感知层对输入层的4类信息进行分类，预处理后交给决策层进行路线选择。分类后的信息主要为5种：主观确定信息(Sub_cert)、主观模糊信息(Sub_fuzzy)、客观确定信息(Obj_cert)、客观随机信息(Obj_rand)、客观模糊信息(Obj_fuzzy)。主观确定信息指驾驶员的主观想法，这里主要指路线偏好。主观模糊信息指驾驶员本身无法用具体数值表示的特性，需要进行模糊化处理，这里主要指驾驶员的拥塞避免指数。客观确定信息指驾驶员所处环境的确定信息，不需要进行处理就能得到。客观随机信息指由于驾驶员不同认知能力，存在随机偏差的感知信息，这里主要指驾驶员对路网熟悉程度不同导致的不同感知阻抗。客观模糊信息指所处环境中驾驶员无法定量表示的模糊变量，这里主要指道路车流量密度。

　　感知层对分类信息的预处理函数假设如下：

　　Sub_cert=f_sc(Prefer) (1)

　　Sub_fuzzy=f_sb(Fami,Wred)(2)

　　Obj_cert=

　　f_oc(Sum_lane,N_lane,T_green,V_max,V_self,Loc)(3)

　　Obj_rand =f_or(Fami,Li,Ci,T_freei, Volume)(4)

　　Obj_fuzzy=

　　f_of(Self_densi,Neib_densi,V_fro,V_neib,D_fro,D_neib)(5)

　　主观确定信息处理函数f_sc和客观确定信息处理函数f_oc由于无需对信息进行处理，结果等于输入信息，f_sc和f_oc为：

　　f_sc=x(6)

　　f_oc=x(7)

　　客观随机信息处理函数f_or需要考虑驾驶员本身的认知能力，驾驶员对路网熟悉程度不同，对路段的感知阻抗也不同，会选择不同的感知最优路径。路网熟悉程度Fami∈(0,1)，Fami值越大，感知阻抗R越接近真实阻抗，则f_or为：

　　f_or=R=x［1±(random(1-Fami))］(8)

　　其中，+或-由驾驶员特性决定。当驾驶员路线偏好为路径最短(Prefer = Shortest_path)时，阻抗考虑路段长度，R=L［1±(random(1-Fami))］。当驾驶员路线偏好为时间最短(Prefer =Shortest_time)时，阻抗考虑路段行驶时间，R= T［1±(random(1-Fami))］。其中T=T_free［1+α(Volumn/C)β］，路段行驶时间随交通量的变化而改变。

　　对主观模糊信息处理函数f_sb和客观模糊信息处理函数f_of采用模糊判断的方法。驾驶员根据自身的感知对内在因素和周围环境信息做出判断。主观模糊信息和客观模糊信息预处理后，相应变量如拥塞避免指数(Wred)、本车道密度(Self_densi)、相邻车道密度(Neib_densi)、变道条件(Lane_changing)可取值为高(High)、中(Mid)、低(Low)。

　　决策层是驾驶员对预处理信息的思维决策过程。不同路线偏好的驾驶员依据对路网的整体了解，选择感知阻抗最小的路线为最优路线，行驶过程中，周围环境和邻居代理可能对驾驶员路线偏好产生影响，不同拥塞避免指数的驾驶员可能改变路线、变更车道和车速。

　　变更路线的模糊规则如下：规则1：if  Wred=High &［ Self_densi=High &(Neib_densi=Mid || Neib_densi=Low)］ || (Self_densi=Mid &Neib_densi=Low) & (Lane_changing=Sati ||Lane_changing=Just_sati) &［ random(1)<p1 ］, then change path

　　规则2：if  Wred=Mid &Self_densi=High &Neib_densi=Low &Lane_changing=Sati&［ random(1)<p2 ］ , then change path

　　规则3：if  Wred=Low &Self_densi=High &Neib_densi=Low &Lane_changing=Sati &［ random(1)<p3 ］, then change path

　　规则4：others ,then continue driving

　　p1、p2、p3分别是拥塞避免指数为高、中、低驾驶员在满足变更路线条件下变更路线的概率，可由调查获得。

　　输出层主要是驾驶员决策后的行为表现和偏好影响，行为表现体现在下一行驶路段、车道、车速的变化，路线偏好受驾驶员本身拥塞避免指数和长时间路网拥塞的影响。

2基于智能代理的动态交通分配

　　确定驾驶员智能路线决策机制后，OD矩阵所对应的驾驶员便根据决策路线行驶，由此汇聚成整体的交通分配状态。按图3所示流程图实现智能代理的动态交通分配IATAM。

　　图3中，首先根据OD矩阵获得对应驾驶员的起讫点、驾驶员综合个人信息和环境信息后进行智能路线决策，然后依照决策路线行驶，下一刻的路线决策随个人想法和交通环境的变化而不断更新，直到所有驾驶员到达目的地。

3实验与分析

　　3.1实验目的与方法

　　本文的实验目的是对所构建的动态交通分配模型IATAM进行仿真和分析。主要分为以下两点：一是通过对IATAM模型与其他模型交通分配后的路段流量与路网采集真实数据的对比，表明IATAM模型结果精度更高；二是对相同目的地驾驶员行驶路线总数的分析，表明驾驶员路线选择的随机性。

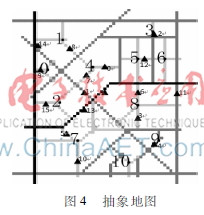
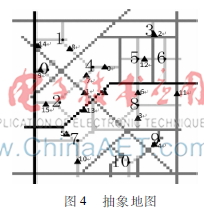
　　图4抽象地图本文采用Netlogo仿真平台进行模型验证。对南京市鼓楼区部分路网抽象简化，构建图4所示的交通路网。图中圆点表示交通小区中心，三角形表示按OD覆盖和最大流量比原则［8］设置的检测点，线条颜色越深通行能力越大。按图3所示基于智能代理的动态交通分配流程进行仿真，相关数据通过地图和访问调查获取。

　　3.2实验结果与分析

　　(1)模型误差分析

　　仿真中，将15 min的OD需求分配至交通小区中心，各驾驶员按照IATAM模型行驶向目的地，把IATAM模型检测点车流量与道路实测检测点车流量以及其他分配模型(平衡分配法、比例配流法)进行比较，部分检测点如图5所示，并根据式(9)计算不同模型检测点车流量与道路实测检测点车流量的平均相对误差(Average Relative Error,ARE)。　　

　　IATAM模型ARE=6.42%，比例配流法ARE=9.95%，平衡配流法ARE=11.93%。由于OD矩阵本身的误差，交通分配后的车流量误差无法达到非常小，但IATAM模型相比其他模型精度更高，能更好地模拟真实路网。

　　(2)驾驶员路线选择随机性分析

　　记录仿真中两地间的距离以及两地间所有驾驶员的行驶路线总数。对两地距离进行划分，并对在划分距离内的不同行驶路线总数取平均值。画出IATAM模型平均行驶路线数与两地距离的图像，并与路网实测数据作对比，如图6所示。

　　图6中，随着两地距离的增加，驾驶员的行驶路线总数呈现波动增长趋势，当两地直线距离小于10 000 m时，增长速度较快；当两地直线距离大于10 000 m后，增长速度减缓。图6表明，行驶距离越长，驾驶员路线选择随机性越大。4结论

　　本文对交通分配中的驾驶员路线决策行为进行建模。在建模过程中，依据驾驶员的不同路线偏好，考虑主观信息模糊性和客观信息随机性，结合驾驶员行驶过程中的拥塞避免，提出神经网络结构的路线决策机制。本文提出的IATAM模型很好地体现了交通分配过程中的主观性、不精确性和随机性。然而，IATAM模型仍然存在局限性。在本文基础上，进一步的研究工作可以从以下两方面展开：一是路段阻抗的计算，IATAM模型考虑路线偏好为时间最短时路段阻抗采用美国BPR路阻函数，但实际路网中，影响路段阻抗的因素很多，比如相邻车道车流量、红绿灯情况等，需要修正阻抗函数，从而更加贴近现实；二是交通分配模型的精细化，IATAM模型考虑了道路密度、驾驶员路线偏好、路网熟悉程度、拥塞避免指数等模糊随机变量对路线决策的影响，实际交通分配更为复杂，需要有更多的考虑。

参考文献

　　［1］ 陈彦如,蒲云.用遗传算法解决固定需求交通平衡分配问题［J］.西南交通大学学报(自然科学版),2000,35（1）:4447.

　　［2］ Lu Shiqiang, Dai Shoufeng, Liu Ximin. A discrete traffic kinetic modelintegrating the lagged cell transmission and continuous traffic kinetic models［J］. Transportation Research Part C Emerging Technologies, 2011, 19(2):196205.

　　［3］ 周溪召. 驾驶员实时动态路径选择行为组合模型［J］. 上海理工大学学报, 2002, 24(2):109112.

　　［4］ 王卫卫,赵小梅,李新刚,等.VMS对驾驶员路径选择影响的实证研究与建模［J］.交通运输系统工程与信息,2013,13(3):6064.

　　［5］ 李强, 缪立新, 段进宇. 基于驾驶员路径选择的动态交通仿真模型［J］. 公路交通科技, 2001, 18(6):6569.

　　［6］ 朱大奇.人工神经网络研究现状及其展望［J］.江南大学学报（自然科学版）, 2004, 3(1):103110.

　　［7］ 昌霞, 孙瑜, 冉婕,等. 基于时态的模糊描述逻辑初探［J］. 微型机与应用, 2010,29(6):7577.

　　［8］ 伍建国, 王峰. 城市道路交通数据采集系统检测器优化布点研究［J］. 公路交通科技, 2004, 21(2):8891.