孙汝峰，刘顺兰

　　（杭州电子科技大学 通信工程学院，浙江 杭州 310018）

　　摘要：提出了一种基于高阶累积量和谱分析识别多种数字调制信号的算法。首先根据各调制信号四阶和八阶累积量的不同，定义一个特征参数实现信号的类间识别；其次根据不同调制信号二次方谱与四次方谱的不同，提取出相应的特征参数，从而实现信号的类内识别。仿真实验结果表明，该方法在较低信噪比条件下可以对2/4/8PSK、2/4/8FSK信号实现识别，且识别率较高，具有很强的实用性。

　　关键词：调制识别；高阶累积量；二次方谱；四次方谱

0引言

　　通信信号的调制识别在电子侦察和无线电监控等领域占据着十分重要的地位，主要任务是在调制信息未知的情况下确定调制信号的调制方式以及估计信号的一些参数（如载波频率、波特率等），为之后的信号分析处理提供依据。

　　近年来国内外提出了很多比较有效的调制信号识别方法，主要可以分为决策理论方法和特征参数模式识别方法［1-4］，其中决策论方法需要的先验知识较多［1］，相比较下特征参数模式识别的方法更为实用，常用的特征参数模式分类特征有信号的瞬时特征、高阶累积量特征、小波变换特征、谱相关特征等。参考文献［2］基于信号瞬时特征识别对噪声比较敏感，在低信噪比的环境下识别率比较低。参考文献［3］利用四阶累积量实现2PSK、4PSK和8PSK信号的分类，并证明高阶累积量对信号星座图的平移，尺度和相位旋转等变换具有不变性。这种方法对于识别少数的信号具有不错的性能，但是对于识别较多的调制信号仅仅基于高阶累积量特征的识别需要信号序列的统计信息，需要较大的样本空间才能得到良好的识别效果，无疑增加了算法复杂度，并且MFSK信号的高阶累积量值都相同，直接运用高阶累积量无法识别出MFSK信号。参考文献［4］基于小波变换，则需要信号精确的相位信息。参考文献［5］通过分析信号的谱相关平面图，提取出一组谱相关特征参数来实现对信号的识别。

　　本文提出一种基于高阶累积量与谱分析的调制识别方法。利用高阶累积量提取更少的特征参数对信号进行类间识别。利用不同信号经过非线性变换后谱线特征的不同提取信号的特征参数对信号进行类内识别,在低信噪比环境下实现更高的识别率。计算机仿真结果验证了算法的实用性和有效性。

1信号模型

　　一般情况下接收到的受噪声污染过的数字调制信号的模型可表示为［5］：

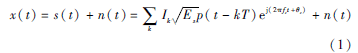
　　其中，k=1,2,3,...,N,N为发送码元序列的长度，Ik表示码元序列，p(t)为基带码元波形，T为码元宽度，fc为载波频率，θc为载波相位，Es为发送码元波形的能量,n(t)为零均值的高斯白噪声。

　　接收端对接收信号进行预处理，假设载波频率、相位、定时同步，下变频后的复基带信号可以表示为［6］:

　　其中，Δθc为载波相位差。

　　调制信号的类型不同，Ik的表达形式也不一样，具体如下：

　　对MPSK信号：

　　Ik=ak+jbk∈{ej2π(m－1)/M,m=1,2,...,M}(3)

　　对MFSK信号：

　　Ik=ej2πfkt(4)

　　其中，fk∈{(2m－1－M)Δf,m=1,2,...,M} ，Δf为信号的频率间隔。

2高阶累积量和高阶矩

　　对于一个具有零均值的复随机过程X(t)，其高阶矩定义为［7］：

　　Mpq=E［X(t)(p－q)X*(t)q］(5)

　　其中，E［·］表示求期望运算。

　　累积量定义为［8］：

　　Cpq=Cum{X(t),…,X(t),X*(t),…,X*(t)}(6)

　　其中，X(t)为p－q项，X*(t)为q项。Cum为累积矩，* 表示函数的共轭。

　　常用的累积量与矩的关系如下［9］：

　　C20=M20(7)

　　C21=M21(8)

　　C40=M40－3M220(9)

　　C42=M42－|M20|2－2M221(10)

　　C60=M60－15M40M20+30M320(11)

　　C63=M63－6M41M20－9M42M21+18M220M21+12M321(12)

　　C80=M80－28M20M60－35M240+420M220M40－630M420(13)

　　因发送信号s(t)与高斯白噪声n(t)两者独立，根据累积量的性质由式（1）可得：

　　Cum(x(t))=Cum(s(t))+Cum(n(t))(14)

　　由于零均值高斯白噪声大于二阶的累积量值为零，则式(14)也可表示为：Cum(x(t))=Cum(s(t))。即接收信号的高阶累积量值等于发送信号的高阶累积量值，据此可以消除高斯白噪声的影响。

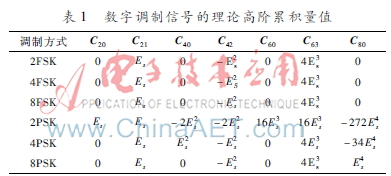
　　假设符号发送概率相等，信号能量为Es，且无高斯噪声影响，采用总体平均代替统计平均的方法［10］，可以得到各种调制信号的高阶累积量理论值，具体如表1所示。

3基于信号高阶累积量实现调制信号的类间识别

　　分析表1可以看出，MFSK与MPSK的C80值存在着较大的差别，可以利用C80这个值实现MFSK与MPSK的类间识别。本文定义特征参数F如下：

　　特征参数选取信号的八阶和四阶累积量，可以减小噪声的影响，采用绝对值形式可以减小相位抖动对特征参数的影响，采用比值的形式可以消除幅度对特征参数的影响。根据表1可以得到各调制信号的F值，具体如表2所示。

　　4调制信号的谱线特征

　　由于不同的调制信号经过非线性变换后，其频谱会呈现不一样的谱线特征，因此利用谱线特征可以实现信号的类内识别。

　　4.1MPSK的二次方谱与四次方谱的谱线特征

　　对于4PSK信号，表达形式如式(2)所示，Ik如式(3)所示。不失一般性，其中ak+jbk∈22{1+j,1－j,－1+j,－1－j}，p(t)为升余弦型脉冲，滚降系数α取0<α<0.5，并假设Δθc=0。则信号二次方形式的统计期望值为：

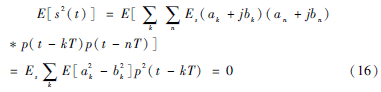
　　参考文献［11］分析了信号的谱线生成特性，当E［s2(t)］具有周期时变性时，其频域（二次方谱）会产生出离散的谱线。而对4PSK信号，由式(16)可知E［s2(t)］=0，因此不具有周期时变性，所以其二次方谱不存在离散谱线。

　　同理，4PSK四次方形式的统计期望值为：

　　式(17)是一个以T为周期的函数，其频域会产生离散谱线，相应的傅里叶变换形式（信号的四次方谱）为：

　　同理可以分析得到，2PSK信号的二次方谱和四次方谱均存在谱线，8PSK信号的二次与四次方谱均不存在谱线。图1给出了无噪声干扰下4PSK的谱线特征图。

　　4.2MFSK的二次方谱的谱线特征

　　根据之前分析，MFSK的等效复低通信号形式可用式(2)表示，其中Ik用式(4)表示。不失一般性，p(t)为升余弦型脉冲［12］，滚降系数α取0<α<0.5。以2FSK信号为例，2FSK信号做二次方谱为：

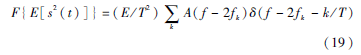
　　其中，A(f)=F{p2(t)}，由于α<0.5的限制，由式(19)可知2FSK信号的二次方谱在±2Δf处有两条明显谱线。同理分析可得，4FSK信号的二次方谱在±2Δf、±6Δf处有4条谱线，8FSK信号的二次方谱在±2Δf,±6Δf,±10Δf,±14Δf处有8条谱线。

　　5基于信号的谱线特征实现调制信号的类内识别

　　对于MPSK信号，由于其不同阶数的PSK信号特征参数F的值不同，可以通过本文定义的F值实现类内识别。但是本文建议采用MPSK信号的二次方谱和四次方谱零频处是否存在谱线作为识别特征值。如果信号的二次方谱在零频位置处存在谱线，令其特征参数f1=1，否则f1=0。如果信号的四次方谱在零频位置处存在谱线，令其特征参数f2=1，否则f2=0。定义N_p=［f1,f2］，据之前的分析，MPSK信号的N_p值表示如下：

　　由式(20)可以实现MPSK信号的类内识别。

　　对于MFSK信号，由于其二次方谱的谱线个数对应信号的M值，因此这里提取特征参数N_f，如果其所测信号二次方谱中谱线的个数N_f=2，则为2FSK信号；如果N_f=4，则为4FSK信号；如果N_f=8，则为8FSK信号。

　　本文建议的基于高阶累积量和谱分析的数字调制信号识别流程图如图2所示。

6性能仿真与分析

　　设MPSK、MFSK信号的载波频率为5 kHz,采样频率为40 kHz，码元速率为1 000 b/s，且MFSK的频率间隔为5 kHz，数据长度N=2 000，加性噪声为高斯白噪声。在相同的信噪比环境下，对信号进行100次独立试验［1314］。

　　由于特征参数F的幅度范围比较大，为观察方便，将其划分为两段（［05］,［2080］）。分别绘制出调制信号的特征参数F随信噪比变化曲线，如图3所示。

　　从图3可以看出，MFSK与MPSK信号的F值都比较接近于前面计算的理论值，两者的F值存在着较为明显的差别，这就说明了可以利用F值来实现两者的类间识别。选取F=1作为类间识别的阈值，当信号的F值大于1的时候，信号判定为MPSK信号，否则判定为MFSK信号。

　　在实现MFSK与MPSK信号的类间识别仿真之后，利用上述所提的特征参数根据算法流程对两者进行类内识别的仿真。同一信噪比，对所有信号进行500次独立试验，取识别正确的次数和识别总次数的比值为信号的识别率，取信号的类间识别率与类内识别率的乘积作为信号的总识别率，仿真结果如图4所示。

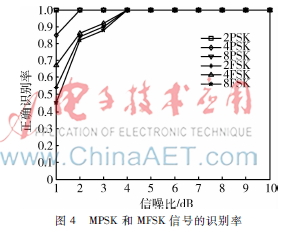
　　由图4可知，采用本文建议的方法，MPSK信号在信噪比为1 dB情况下，2PSK、4PSK、8PSK信号的识别率分别为100%、85%、100%；当信噪比大于2 dB时，3种PSK信号的识别率都达到了100%。MFSK信号在信噪比为1 dB的情况下，2FSK、4FSK、8FSK信号的识别率分别为54%、67%、45%；当信噪比等于3 dB时，3种FSK信号信号的识别率达到了85%以上；当信噪比大于等于4 dB时，3种FSK信号信号的识别率达到了100%。由此可见，本文建议的方法在低信噪比下也取得了较高的识别率。MFSK信号的识别率在信噪比较低的情况下比MPSK信号的识别率要低，分析原因主要是因为受噪声影响类间识别的特征值F在信噪比低的情况下要比理论值偏大，在对MFSK信号识别时，会出现大于阈值的情况，导致判断出错。

　　参考文献［9］中分别采用高阶累积量的特征值和微分后的累积量构造特征值的方法来识别MPSK和MFSK信号，在相同的仿真实验环境和信号参数设置，本文方法与参考文献［9］进行性能对比试验，其对比结果如表3所示。从表3可以看出，相比参考文献［9］，在相同条件下本文所提方法的识别性能显著提高。 

7结论

　　本文基于高阶累积量和谱分析的理论知识，定义了一个基于信号八阶累积量和四阶累积量的特征参数F，用来实现MFSK和MPSK信号的类间识别。由于高斯白噪声高于二阶的累积量值为零，因此此方法具有很好的抗噪声性能。根据不同信号的二次方谱与四次方谱的谱线特性不同，分别提取出特征参数N_p和N_f对MPSK和MFSK信号实现类内识别。计算机仿真结果表明，此方法在低信噪比的情况下可以取得理想的识别率，证明了此方法的有效性，抗噪声性能较强。

参考文献

　　［1］ NANDI A K,AZZOUZ E E.Algorithms for automatic modulation recognition of communication signals［J］.IEEE Transactions on Communication, 1998, 46(4):431436.

　　［2］ 位小记，谢红，郭慧.基于瞬时特征参数的数字调制识别算法［J］. 传感器与微系统，2011,30（1）：127130.

　　［3］ 陈卫东，杨绍全.利用累量不变量对MPSK信号分类［J］.西安电子科技大学学报，2002，29（2）：229232.

　　［4］ 胡建伟，汤建龙，杨绍全.使用小波变换的MPSK信号调制类型识别［J］.电路与系统学报，2006,11（3），130134.

　　［5］ 韩国栋，蔡斌，邬江兴.调制分析与识别的谱相关方法［J］.系统工程与电子技术，2001,23（3）：3436.

　　［6］ 徐晓瑶，刘娟,杨东.多径信道下MPSK 信号调制识别算法的研究［J］.电子技术应用，2010,36(2):103106.

　　［7］ PROAKIS J G． Digital communicatio （4th edition）［M］． NewYork: McGrawHillBook Co．，2001．

　　［8］ 刘献玲.基于累量的OFDM信号调制识别［D］.西安：西安科技大学，2007.