0 引言

    近年来，随着科学技术的迅速发展，各生产系统的结构日益复杂化，各种高精度、集成化设备广泛应用于生产线。企业间的竞争越来越激烈，生产系统的复杂性、随机性使得生产线的维护难度不断提升，维护成本和强度随之加大，合理的维护策略对获得良好生产效益起着至关重要的作用。

    目前国内外关于生产线维护策略的研究成果很多，主要分为基于状态的维护和基于时间的维护两种形式^[1]。基于状态的维护是在设备检测技术迅速发展的基础上实现的，通过检测设备的状态来判断其出现故障的概率，确定实施方案，使损失降到最低。传统的基于时间的维护多采用固定维修周期，这样的方式操作简单，维护人员和备件都可以做事先安排。随着神经网络与模糊系统理论与技术的发展，基于神经网络与模糊逻辑的自适应控制系统得到了广泛应用^[2-5]。徐昕等人^[6]对基于MDP动态系统学习控制理论、算法与应用的发展前景进行综述。起初研究人员用离散的Markov链描述设备维护调度模型，之后，Gharbi等人提出用连续Markov链描述设备寿命的维护结构，通过控制设备生产率和预维修率使目标函数达到最优化^[7]。Jin 等人^[8]利用马尔可夫决策过程描述设备维修或替换等维护活动的概率转移函数，得到一个生产系统的预防性维护优化模型。陈静静提出利用MDP模型同时考虑劣化故障和随机故障两种故障类型，制定针对单台设备工作排序、清洗和维修的长期维护优化策略^[9]。以上关于MDP模型的应用多采用固定式转移概率，在一定程度上反映了状态的变化过程。根据生产实际可以考虑采用动态的转移概率反映不同状态下的状态转移情况。

    本文将利用连续时间的MDP模型描述单台设备工作状态，充分体现生产实际中设备工作、维护的连续性，综合考虑转移概率和实施方案选择的动态性和随机性，利用MATLAB实现优化获取最佳维护周期。在系统层维护中以混联结构为框架应用该模型，对其实现优化仿真，验证其可行性。

1 连续时间的MDP模型

    作为描述动态随机系统优化决策问题的一类基本数学模型，MDP模型通常用四元组{S，A，P，R}表示，其中S为状态空间，A为行为空间，P为转移概率（满足无后效性），R为回报函数，在一定意义上可以理解为目标函数。

    定义行为策略π表示从状态集合S到行为选择概率的映射，即π：S→P(a)。

1.1 离散空间的MDP

1.2 连续时间的MDP

其中，r为回报函数，对于其积分即为目标函数。需要寻找最佳π使V^π(x)达到最优解。

    实际生产系统中设备工作环境复杂，设备的自身工作状态、运转环境、已维护次数等信息直接关系生产线的效益，合理的维护策略和预先安排能够有效降低因突发事件带来的巨大损失。MDP模型能够形象地模拟不同维护策略对设备状态的影响。对于整个生产系统，要获得最优维护策略，首先需要研究每台设备的维护策略。本文利用连续时间的MDP模型研究单台设备维护策略，然后研究在交货期、在制品数和成品率等因素的综合影响下，系统层的维护策略。

2 单台设备维护策略

    在生产实际中设备的工作状态具有连续性的特点，因此，利用连续时间的MDP模型能够更加合理地模拟设备退化过程。在连续时间的MDP模型中，状态空间、行为空间均为连续空间，状态转移时间也是连续的。本文将在此基础上进一步考虑转移概率的动态性和方案选择的随机性。本文将设备的状态空间设定为连续空间，综合考虑设备自身运转状态、成品率、维修记录等因素，利用连续函数拟合设备自然状态下的退化过程，实现设备整个生命周期中状态的连续性。

    首先，根据生产实际数据拟合状态空间x(τ)，0<τ≤m。x(τ)是关于自然退化时间τ的连续函数，表示设备的自然退化过程。根据实际情况，状态空间x(τ)为递减函数。随着时间的延续，当到达时刻m时设备将退化至某一劣化极限x(m)，状态x(m)表示设备出现故障，必须进行故障性维修。

    行为空间u(t)表示t时刻系统处于状态x(τ)可采用的行为的集合。

且当 x(τ)=x(m)时u(t)=1，当x(τ)<x(m)时设备处于无法修复状态，停止工作。

    状态转移矩阵P(i，j，a)表示设备处于状态x(i)，采用方案a后，设备状态转移到x(j)的概率，其中i，j∈τ。转移概率P(i，j，a)的随机性表现为：

    r(x(τ)，u(t))表示设备处于状态x(τ)时采用方案u(t)获得的收益。π(u(t))表示所采用的一系列维护策略，即在每个维护时刻所采用的方案，目标即为寻找一个最优维护策略π^*(u(t))使效益最大化。本文中维护策略π的选择由转移概率的动态性和方案选择的随机性体现。在此基础上确定最优维护周期T，使目标函数达到最优解。

    平稳策略的值函数：

    若u(t)≡0则设备状态变化过程为服从函数x(τ)，即设备自然退化过程。且有，若采用最优维护策略π^*(u(t))，则所对应的状态空间为x^*(τ)。目标即为寻找最优维护策略π^*(u(t))和最优维护周期T^*使系统效益最大化。

    假设维护周期为l，采用一定维护策略后，单位时间产生的效益为h(t)，其与状态空间具有线性关系。则一个维护周期内获得效益：

其中g(a)表示选择方案a的概率，x(i)表示设备所处状态。最佳维护策略π^*即使效益最大化的维护周期T和实施方案a，π^*π(T，a₁，a₂，a₃，…，a_n)，a_n∈a。

    目标函数：

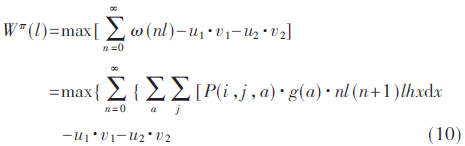
其中，u₁、u₂分别表示设备进行一次预防性维修和故障性维修的费用，v₁、v₂分别表示设备进行预防性维修和故障性维修的次数。

3 系统层维护策略

    对于生产系统，根据连接形式的不同各单台设备所得效益在系统层效益中反映的程度不同。本文研究假设，对于串联结构的效益，以串联结构中效益最大的单台设备的效益作为评价标准。并联结构的效益，以各单台设备效益之和为评价标准。

    串联系统效益：

    在系统混联结构中，将并联设备作为一个单元与串联设备一起作为串联结构考虑。

    混联系统效益：

    本文以混联结构为模型框架研究最优维护策略，系统层维护策略模型满足maxQ^π(l)，即获得能够使系统效益最大化的维护周期l和相应的各个周期的实施方案。

4 案例仿真

    为验证模型的可行性和有效性，本文采用以下算例进行分析。如图1所示，系统由5台退化模型相同的设备组成，按统一周期进行仿真。设备自然退化过程x(τ)通过拟合为8次多项式，极限工作时间8 000。一次故障性维修的费用u₂=5 000元，一次预防性维修的费用u₁=1 000元。转移概率P(i，j，a)的分布如下：

    实施方案选择原则如下：

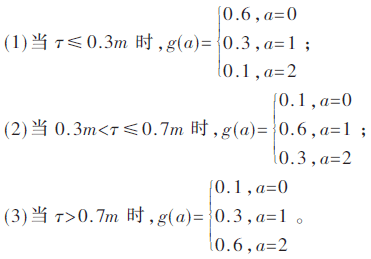
    利用MATLAB建模仿真获得如图2结果。由图2可知，在此模型假设基础上，当维护周期为1 700 h时效益最大化。维护周期较低时，频繁的维护会增加维护费用导致效益降低。维护周期太大时，设备维护不及时，故障停机的概率增加，设备利用率下降，导致效益下降。

    由图3可知，在设备运转初期（0<t<2 500），当到达维护周期时选择正常运转（a=0）而不实施维护措施的概率为40%；在运转中期（2 500<t<5 600）,选择预防性维护（a=1）的概率为61%；在运转后期（t>5 600）,选择故障性维护（a=2）的概率为54%。由此可知，在设备运行后期随着设备可靠性的降低，故障维修的次数增加，符合生产实际，证明方案选择假设可行。

    本文以混联结构为框架应用此模型，分析系统的设备利用率，与基于离散空间的MDP维护策略进行比较。如图4所示，采用连续时间MDP模型下的平均利用率为0.992 48，采用离散MDP模型的平均利用率为0.987 22。由此可知，连续时间MDP模型下的维护策略能够有效提高设备利用率，从而在一定程度上提高效益，进一步证明基于连续时间MDP模型的维护决策的有效性和可行性。

5 结论

    在生产实际中设备状态属于连续变化量，本文采用连续时间的MDP模型模拟设备状态连续变化过程下系统效益的连续变化过程。综合考虑生产实际因素，利用生产实际数据模拟设备自然退化过程，将连续变化的设备状态转化为效益的变化过程，以效益最大化为目标获得最优维护策略。系统层框架结构在基于连续时间的MDP模型下，将生产系统的现实因素融于控制条件，进一步控制维护策略，获得较为合理的维护策略。仿真结果显示，基于连续时间MDP模型应用于生产系统，可有效提高设备利用率和产量，改善系统性能，从而提高生产线效益。

参考文献

[1] 吴洪飞.基于非齐次马尔可夫过程的多动作动态维护策略研究[D].上海：上海交通大学，2008.

[2] 王振雷.模糊神经网络理论及其在复杂系统中的应用研究[D].沈阳：东北大学，2002.

[3] 徐瑜，危韧勇.神经网络在控制系统中的应用现状及展望[J].电脑知识与技术，2006(5)：178-179，187.

[4] 徐英智.一种新型模糊神经网络及其在控制中的应用[D].西安：西安电子科技大学，2008.

[5] 马俊伟.动态模糊神经网络在非线性系统中的应用研究[D].沈阳：东北大学，2010.

[6] 徐昕，沈栋，高岩青，等.基于马氏决策过程模型的动态系统学习控制：研究前沿与展望[J].自动化学报，2012(5)：673-687.

[7] GHARBI A，KENNE′ J P.Maintenance scheduling and production control of multiple-machine manufacturing systems[J].Computers & Industrial Engineering，2005(48)：693-707.

[8] JIN Y L，JIANG Z H，HOU W R.Optimal policy research on reliability-centered preventive maintenance for multicomponents equipment[J].Journal of Shanghai Jiaotong University，2006，40(12)：2051-2056.

[9] 陈静静.基于MDP的半导体制造设备维护调度研究[J].电子测量技术，2012(3)：24-27.