0 引言

    由于成像环境不理想以及成像设备硬件分辨率有限等多种因素会导致图像出现模糊、噪声等问题，导致获取不到超分辨率图像^[1]。故学者们提出了多帧超分辨率图像重构方法，利用低分辨率图像序列间某种类别的附加信息进行互补重构，获取无法辨识的细节信息从而转换成高分辨率图像^[2-3]。

    基于学习以及基于插值技术的重构方法为目前较常用的超分辨率图像重构方法。如Ahmadreza^[4]等人利用各向同性高斯滤波器，对输入图像像素的结构张量进行计算，再利用结构张量插值法实现重构，实验表明该方法能获得质量较高的重构图像。贾茜^[5]等人通过轮廓模板插值算法对低分辨率图像进行放大，然后将所得图像用MCA模型分解，最后将处理后的图像进行合成，从而完成超分辨率图像重构。实验结果表明该方法有效提高了图像锐度，重构效果佳。虽然基于插值法的重构算法实现快速易行，对超分辨率图像重构也有一定的效果，但由于插值过程所固有的平滑效应，导致得到的重构图像存在棋盘和振铃效应。

    对此，樊博^[6]等人利用两步迭代算法和全变分正则化实现超分辨率图像重构，利用两步迭代收缩得到新的估值，最后利用全变分实现重构，实验表明该算法能够较好地实现图像的重构。首照宇^[7]提出了一种改进的基于字典的重构算法，通过引入联合训练思想确保高、低分辨率图像具有相同的表示系数，利用迭代反投影增强重建约束实现重构，实验结果显示该方法具有较好的重构效果。

    然而，此类算法都是基于学习的超分辨率方法，在重构效果上较插值法都有所提高，但是由于计算的复杂性导致该类方法实现复杂，效率较低。

    对此，本文提出了增益映射控制耦合局部正则化的图像重构算法。首先，通过对低分辨率图像中亚像素的移动进行分析；然后，构造正则化算子，联合改进的代数重建法求其稳定值；最后，采用基于局部自适应正则化的增益可控方法，建立增益映射，完成超分辨率图像重构，并测试本文算法的重构性能。

1 图像成像模型

    由于拍摄时相机的移动等原因会导致亚像素平移的产生，从而使图像变得不清晰^[8-9]。图1中表示了低分辨率图像[β_x，β_y]中覆盖3个亚像素沿水平和垂直方向平移的示意图。

2 超分辨率图像的估值

    因为方程式组式(10)存在病态特性，所以式(10)是不稳定的，下面将对方程式组式(10)进行求解。

3 迭代算法与正则化

    代数重建法(ART)属于级数展开法的一种并得到了广泛应用^[10]。ART利用L₂范制定了相异度，并且对迭代后得到的每一个元素都进行了更新。由于在进行误差估值时L₁范比L₂范有更好的效果，在此将ART中的相异度改进为用L₁范来制定，那么中第j个元素的第(n+1)次迭代的表达式如下：

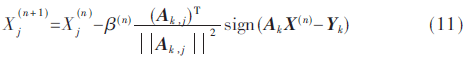
其中j=0，1，2…N-1，k=0，1，2，…K-1，A_k，j是A_k中的第j列元素。迭代参数β⁽ⁿ⁾表示第n次迭代的步长。其中迭代次数n与低分辨率图像指数k有关，其关系为n=k/K。

    正则化被广泛用在求解不稳定线性方程组上，当获得数据的保真度很低时，正则化过程很重要^[11-13]。由于式(10)的不稳定性导致高清图像X的重构存在不稳定性，所以本文将用正则化耦合L₁范的ART来得到改进的ART，从而求解式(10)的稳定解。

    一个获得图像重构稳定解的方法是保持图像空间灰度的同质性^[14-15]。为了获取该稳定解，本文构造一个正则化算子φ(X)，根据高清图像解法的先验知识，可将正则化算子φ(X)与式(8)结合，可得到广义的最小代价函数：

    由图2可见，通过正则化耦合的ART算法迭代后所得图像虽然有一定的重构效果，但是还存在明显的振铃以及模糊效应。下面将采用局部自适应正则化的增益可控方法，建立增益映射，完成超分辨率图像重构。

4 局部自适应正则化及增益映射的建立

    由于边缘高对比度及振铃大小与图像梯度大小成正比，故本文采用自适应技术，使得被估计的高清图像中，每个像素值的正则项和误差项的关系由该像素值的局部信息来控制，从而克服振铃效应和模糊效应。本文采用基于局部自适应正则化的增益可控方法，建立增益映射，完成超分辨率图像重构。

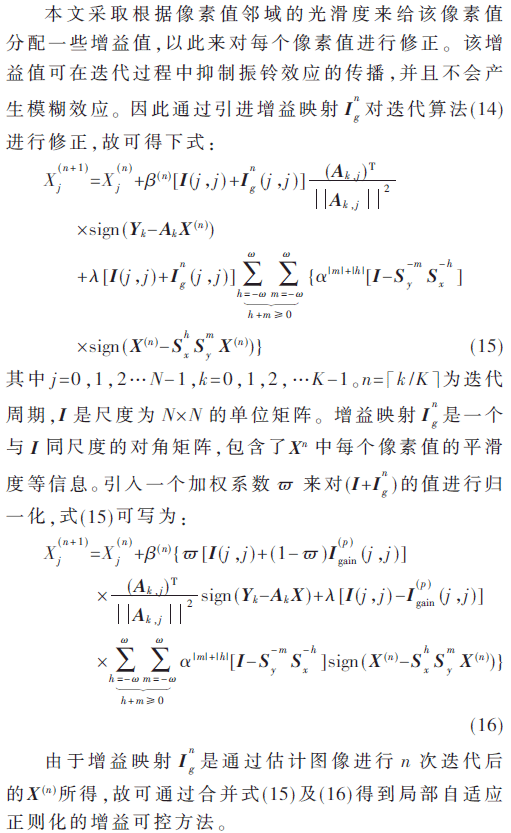
    膨胀-腐蚀现象影响了原始图像的边缘强度，其中图像的膨胀会带来白噪声的影响，图像的腐蚀会带来暗噪声的影响。然而形态学开运算和闭运算，能够在不影响图像边缘锐度的情况下分别移除白噪声和暗噪声^[16-17]。故在此将构造基于增益映射I_g的多尺度形态学。假设Q表示一个圆盘结构元素单元，则rQ定义如下：

其中Z_max和Z_min为Z的最大和最小值，Sigmoid为一个逻辑函数，定义如下：

    (4)通过对Z的像素字典进行排序，获取对角元素，从而形成增益映射I_g。

    结构元素大小的最大值m由估值图像的对比度决定，随着迭代的进行，m将逐渐减少。

    图3展示了本文算法的重构效果对比图，在此m的取值为4，图3(a)为本文算法迭代1次后所得图像，(b)为本文算法迭代10次后所得图像。

5 仿真结果与分析

    采用经过模糊后的图像作为低分辨率图像，模糊算子H采用5×5的加权系数，再将下采样因子D为5的噪声加入目标图像，最后所得被损坏图像为彩色图像和灰度图像作为测试图像，见图4（a）、图5（a）。通过借助MATLAB 7.10软件来测试本文超分辨率图像重构机制，为了体现本文机制有效性与优异性，将文献[18]和文献[19]的重构方法作对照。

5.1 不同机制对彩色图像重构的质量对比分析

    图4为不同图像重构机制对图4（a）重构后的效果图。可见在对低分辨率彩色图像重构时，本文机制的重构质量最佳，见图4（d）；而对照组的两种图像重构算法重构的图像显然存在振铃和模糊效应，见图4（b）和图4（c）。原因是本文重构机制采用自适应技术，使得被估计的高清图像中，每个像素值的正则项和误差项的关系由该像素值的局部信息来控制，从而克服振铃效应和模糊效应。

5.2 不同机制对灰色图像重构的质量对比

    从视觉效果图对比可见，在对低分辨率灰色图像重构时，本文机制的重构质量最佳，见图5（d），图像清晰度较好；而对照组的两种图像重构算法的复原图像质量不佳，分别见图5（b）与图5（c），较为模糊，丧失了部分纹理信息。

5.3 量化分析

    将不同程度的噪声加入到图4的低分率图像中，然后用不同重构算法来处理这些图像，最后通过得到的PSNR来对不同机制的重构效果进行量化分析，PSNR量化图如图6所示。从图中可见，本文重构机制优于对照组的机制，原因是本文采用了基于增益映射I_g的多尺度形态学，能够在不影响图像边缘锐度的情况下分别移除白噪声和暗噪声，从而保持了边缘锐度提高了PSNR，保持了图像的结构相似度。

6 结论

    本文提出了基于局部自适应正则化的图像重构算法。通过对低分辨率图像中亚像素的移动进行分析，确定高低分辨率图像间的形成模型, 将重构问题转化为一个不稳定的线性方程式组；然后构造正则化算子，联合改进的代数重建法求其稳定值；最后采用基于局部自适应正则化的增益可控方法，完成超分辨率图像重构。仿真结果表明，本文机制拥有更好的重构效果，有效降低了模糊与振铃效应。

参考文献

[1] CHENG P，QIU Y Y，ZHAO K，et al.A transductive graphical model for single image super-resolution[J].Elsevier Neurocomputing，2015，148(1)：376-387.

[2] POLATKAN G，BLEI D，DAUBECHIES I.A bayesian nonparametric approach to image super-resolution[J].Pattern Analysis and Machine Intelligence，2015，37(2)：346-358.

[3] ROYLE S J.Super-duper resolution imaging of mitotic microtubules[J].Nature Reviews Molecular Cell Biology，2015，16(2)：67-76.

[4] BAGHAIE A，Yu Zeyun.Structure tensor based image interpolation method[J].AEU Electronics and Communications，2015，69(2)：515-522.

[5] 贾茜，易本顺，肖进胜.基于结构成分双向扩散的图像插值算法[J].电子与信息学报，2014，36(11)：2541-2548.

[6] 樊博，杨晓梅，胡学姝.基于压缩感知的超分辨率图像重建[J].计算机应用，2013，33(2)：480-483.

[7] 首照宇，廖敏璐，陈利霞.改进的基于稀疏表示的图像超分辨率重建算法[J].计算机应用与软件，2014，31(4)：201-204.

[8] XUN Z J.A fixed-point method for a class of super-large scale nonlinear complementarities problems[J].Computers & Mathematics with Applications，2014，67(5)：999-1015.

[9] MAISELI B，ALLY N，Gao Huijun.A noise-suppressing and edge-preserving multiframe super-resolution image reconstruction method[J].Signal Processing，2015(34)：1-13.

[10] PRUN V E，NIKOLAEV D P，BUZMAKOV A V，et al.Effective regularized algebraic reconstruction technique for computed tomography[J].Crystallography Reports，2013，58(7)：1063-1066.

[11] 张晓克，许建刚.超分辨率图像重建技术研究[J].科技创新与应用，2014，32(11)：68-69.

[12] 刘哲，张永亮，郝珉慧.一种快速的超分辨率图像重构算法[J].光电子.激光，2013，24(2)：372-377.

[13] PENG H，RAO R，DIANAT S.Multispectral image denoising with optimized vector bilateral filter[J].Image Process，2014，23(1)：264-273.

[14] KYUNGSHIN D，SHIKMOON Y.Super-resolution image reconstruction using wavelet based patch and discrete wavelet transform[J].Journal of Signal Processing Systems，2015，81(1)：71-81.

[15] SALGADO C，DOLUI S，MICHAILOVICH V.Reconstruction of hardy data using a split Bergman optimization approach[J].Image Analysis and Recognition，2013，50(1)：589-596.

[16] KUMAR B K S.Image fusion based on pixel significance using cross bilateral filter[J].Image and Video Processing，2013，5(9)：1193-1204.

[17] YIN W，OSHER S，GOLDFARB D，et al.Bregman iterative algorithms for L1-minimization with applications to compressed sensing[J].SIAM J Image Science，2008，1(1)：143-168.

[18] WUNDERLI T.Total variation time flow with quantile regression for image restoration[J].Mathematical Analysis and Applications，2013，403(1)：272-282.

[19] ZHOU L，LU X B，XUE T.A local structure adaptive super-resolution reconstruction method based on BTV regularization[J].Multimedia Tools and Applications，2014，71(3)：1879-1892.