0 引言

    在计算机辅助设计系统中，传感器的设计效率以及测量传感器对于不同系统的普适性很大程度上取决于电子元件模型的准确性^[1]。由于电子元件对于安装条件的依赖性，作为模型效率的重要评价参数，其高频参数估计具有很大的依赖性。此外，该模型还要考虑如何使模型参数保持足够的稳定性。与此同时，神经网络作为一种常用的建模工具将被采用，并以无源电子元件为例研究建立性能优异的神经网络模型。

    影响神经网络模型精度的主要因素有两个：一是良好的网络拓扑结构；二是优异的参数学习算法。目前经典的算法是反向传播（BP）学习算法^[2]，但是BP算法采用的最速下降算法容易使参数陷于局部极值而无法跳出，如何进行参数的全局寻优是提高神经网络应用效果的关键。由于该缺点的存在导致即使具有较好的网络拓扑结构也存在性能表现不佳的情况出现。

    为解决这个问题，有关学者对智能优化算法应用到神经网络参数优化进行很多研究。如文献[3~5]等分别结合差分进化、遗传算法和粒子群算法对神经网络进行参数优化，取得一定效果。本文相对于上述文献的创新点在于，一是采用和声搜索算法对神经网络参数进行优化，采用高斯方式对和声搜索算法进行改进，并且给出其理论分析；二是设计泛函连接模糊神经网络拓扑结构，利用泛函连接作为模糊神经网络的模糊规则，力求获得更加准确的模型。

1 泛函链接模糊神经网络

    本节主要介绍使用输入变量非线性组合的FLFNN网络结构^[6]。图1给出了该FLFNN网络的结构图，FLNFN模型通过以下形式实现了if-then的模糊规则^[7]：

式中，m_ij、σ_ij分别为FLFNN网络模糊集高斯隶属度函数的均值和方差。

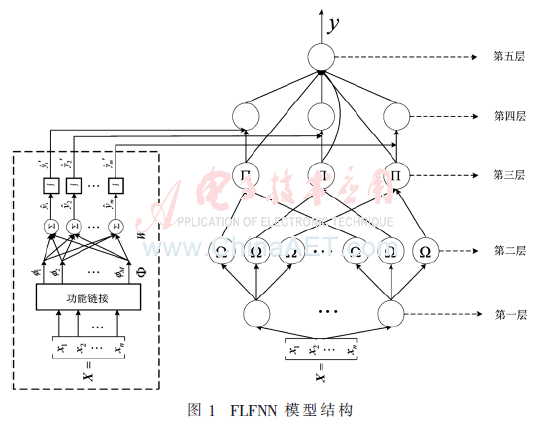
    第三层：该层节点从第二层节点中接收一维隶属度的关联规则，这里的节点操作结果将作为先前描述的模糊规则的先决条件，则该层节点的推理输出规则可表述为：

其中，ω_kj为泛函链接神经网络相应的链接权重，φ_k为输入变量的功能表示，而功能扩展部分采用三角多项式基函数，因此基函数的数量M=3×N，N为输入变量的个数。此外，泛函链接神经网络的输出节点数量取决于FLFNN模型的模糊规则数。

    第五层：该层节点的输出值，相当于是对第三层和第四层节点模糊规则的解模糊作用，其输出形式可表述为^[8]：

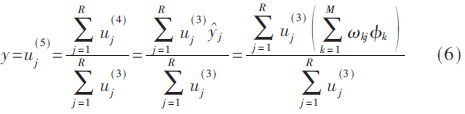
式中，R为模糊规则的数量，y为FLFNN模型的最终输出结果。

2 FLFNN模型学习算法

2.1 标准和声搜索算法

    优化过程与音乐的制作有很多相似的因素，有关学者于2001年提出模仿音乐编写的和声搜索算法^[9-10]。引入和声存储(HM)、存储器大小(HMS)、参照率(HMCR)、间距调整率(PAR)及宽度调整率(bw)等。具体步骤如下^[11]：

    (1)(初始化)目标函数输入向量被存储在向量中，并提供每个输入变量取值范围。HMS大小的向量根据式(16)产生，并存储在HM中：

    (2)(即兴创作)新的向量个体的即兴产生过程可采取如下策略，首先，由算法决定是在HM存储器中选取已有的向量，还是根据HMCR产生一个全新的向量。然后，若选取已有向量，则根据参数PAR和bw对向量进行适当调整(如式(17))。

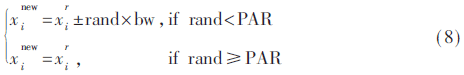
    (3)（HM更新）计算新向量个体及原向量个体的适应度进行对比，采用精英选择策略选取适应度更佳的向量个体，完成对HM的更新。

    (4)(终止判断)检查当前存储的最优向量的适应值是否满足终止条件，如果是则停止算法进化，输出最优值；否则，返回步骤(2)的即兴创作阶段。

2.2 高斯改进和声搜索算法

    文献[8]已证明和声搜索算法已具备很好的收敛速度，尽管如此，和声搜索算法仍然具有改进的余地，如文献[12，13]等。本文首先针对算法中宽度调整率bw为定值，无法反应进化初期和后期的区别的问题，引入变步长bw；其次，将高斯因子引入即兴创作过程。引入控制参数α定义如下：

2.3 理论分析

    为简化理论分析，假设HM中所有的向量xi都是1维的：

式中，[a，b]为向量个体x的搜索空间，x(var)、y(var)分别代表向量x及适应值y的方差。当E(y(var))过大时，算法注重探索能力，但相应地会影响算法收敛，甚至导致算法发散。因为1/HMS取值很小，并且HMCR趋向1，则式(16)可简化为：

    参数α随着迭代的增加逐渐减小，有助于E(y(var))的收敛。而参数g作用是其服从高斯分布，也就是α²g²并非一致性降低的，而是有一定概率增加，这样就有助于平衡算法探索和开发的关系。

3 无源电子元件的FLFNN模型信号检测

3.1 问题描述

    源电子元件的高频参数根据与之连接的设备测量信号结果进行定义，如图2所示。基于矩阵式的去嵌入校准方法可以消除电子元件和测量平面与接触片边界移动的影响（图2中部件6）。

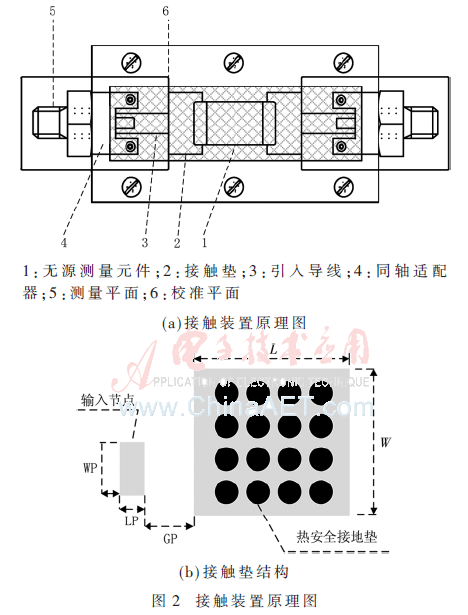
    电子元件的接触焊盘的位置，以及用于形成微波器件的拓扑结构的基板类型和参数在工程师设计过程中都是经常变化的。因此，此类无源电子元件的应用会受到特定测量环境下波散射参数的影响和限制，此外现有的信号检测方法在评估电子元器件的固有参数时效率低下精度不高，在应用到特定系统时会导致较大波动误差的存在。

    因此当前在无源电子元件信号检测中，除了采用常用的波散射参数测量外，研究方向逐渐向无源电子元件模型建立发展。首先，这种模型建立必须考虑电子器件的安装特性（如图3）。其次，必须采用高效简洁的优化算法实现微电子器件的拓扑优化问题。下面将介绍无源电子元件信号检测模型的建立步骤。

3.2 无源电子元件信号模型

    建立该模型的第一步是对FLFNN模型进行编码，使之与和声搜索算法能够顺利对接，图3给出了一种简单的编码方式。其中i、j分别代表第i个输入变量和第j个规则，在本模型中采用高斯隶属度函数，其中该函数的均值和方差将作为变量随同权重ω_kj一起进行编码。m_ij、σ_ij分别代表高斯隶属度函数的均值和方差。则无源电子元件信号检测FLFNN模型的学习步骤如下：

    (1)(编码)首先选取FLFNN神经网络结构中的连接权重ω_kj、高斯隶属度函数的均值m_ij和方差σ_ij作为优化参数来对FLFNN模型进行编码，形式如图3所示。

    (2)(初始化)在搜索空间[0，1]中随机初始化和声搜索算法的种群位置x_p，t(t)，其中下标p=1，2，…，P表示第p个乐章片段，i代表第i个乐符，t代表进化代数，初始化后的种群存储在和声存储器HM中。

    (3)(即兴创作)首先，由算法决定是在HM存储器中选取已有的向量，还是根据HMCR产生一个全新的向量。若产生新向量，其计算公式为：

    (5)(终止判断)检查当前存储的最优乐章的适应值是否满足终止条件，如果是则停止算法进化，输出最优值；否则，返回步骤(3)即兴创作阶段。

4 仿真实验与分析

4.1 高斯和声搜索参数选取

    选取4个通用标准函数对算法进行测试，这4个测试函数均是高维多峰值函数，局部峰值很多，对于种群个体的吸引也较强，测试函数的搜索范围及最优值如表1所示。

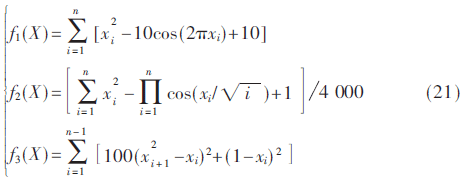
    改进和声搜索算法相对于标准算法增加了控制参数α及高斯分布控制参数g，其中控制参数α受变量λ影响，而高斯分布g主要受方差σ_g影响。其他参数设置为：HMS=100，HMCR=0.95，PAR=0.7，iter=1 500，λ=0.3。仿真结果如图4所示。

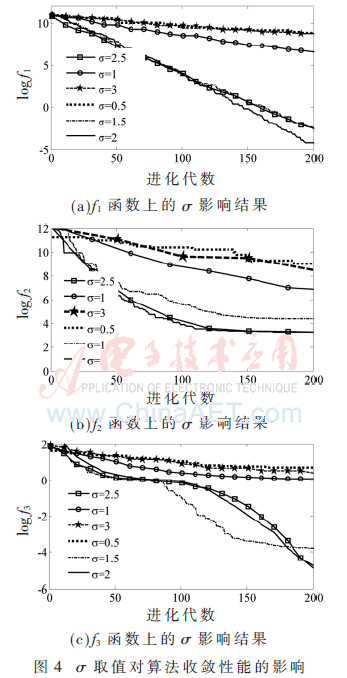
    从图4中可看出，σ_g=2为相对最优的一个取值。可以通过分析式(21)得出σ_g值的大体取值规律，式(21)控制参数?琢的主要作用是使距离宽度调整率（bw）的取值逐渐减小，从而实现在前期选择较大的bw，有利于算法全局搜索，后期选用较小的bw有利于深度开发。但是bw过于规律性的变化，使得某个阶段bw值其实是固定的，这就导致算法缺乏创新性，所以引入高斯分布函数g来打破这种规律化的变化。但是g的取值并非越大或者越小越好，图4仿真给出对比结果，认定σ_g=2为相对最优的取值。

4.2 FLFNN无源电子元件信号检测试验

    图2(b)给出了本实验所采用的安装电阻片接触片的拓扑结构。表2给出的不同规格的电阻器芯片，可通过调整神经网络的参数予以实现，此外表2给出了神经网络的增量学习集。该模型输入参数：绝缘底座厚度、接触垫的几何形状以及频率（0～3 GHz）等^[11，14-15]。神经网络的输出参数包括的电阻器的驻波比。仿真参数设置：HMS=100，HMCR=0.95，PAR=0.7，iter=1 500，λ=0.3，σ_g=2。电磁分析理论已被广泛应用于学习集构造和控制模型的数据质量评价，图5展示了一系列接触垫的结构和绝缘基类型不同配置的电阻器SWR曲线，用来作为FLFNN模型的训练数据。

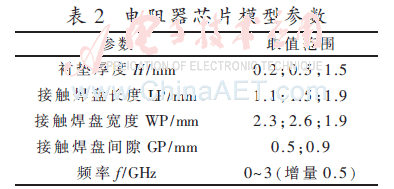
    图5给出了4种不同模型取值参数下的电阻器SWR值曲线，4种参数取值如下：

    case1：WP=2.9 mm，LP=1.9 mm，GP=0.5 mm；

    case2：WP=2.5 mm，LP=1.6 mm，GP=0.8 mm；

    case3：WP=2.3 mm，LP=1.2 mm，GP=0.9 mm；

    case4：WP=2.1 mm，LP=0.8 mm，GP=0.6 mm。

    由图5给出的曲线表明，这些参数对微电子器件的频率特性有明显的影响，进而影响微电子器件的电阻芯片功能。下面主要对3种不同模型的信号检测性能进行仿真对比，对比模型如下：(1)model1：直接信号传输的多层神经网络结构^[16]，在该神经网络学习过程中选取20和14个神经元的两个隐藏层，采用Brent一维搜索算法进行学习。(2)model2：径向基神经网络，该网络结构含有250个神经元^[17]。图6~8给出了所有模型电阻片驻波比(SWR)以及与真实值的偏差(Delta)，测试数据分别在训练集中选取(图6)和不在训练集中选取(图7)，并给出训练集频率以外的预测数据输出对比结果(图8)。

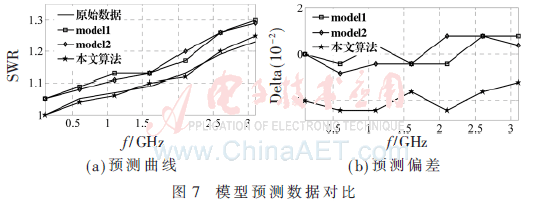
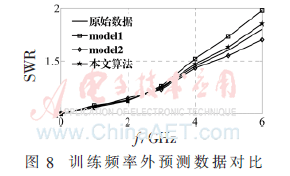
    图6~图8给出了3种有针对性的仿真对比曲线，首先，图6中采用训练数据作为测试数据，无源电子器件设计参数选取case3：WP=2.3 mm，LP=1.2 mm，GP=0.9 mm。图6(a)为预测曲线，(b)为预测曲线与真实曲线的偏差，从图6中可以看出本文算法相对于两种对比算法更接近于真实数据的输出，说明在训练数据作为测试数据情况下，本文算法具有更高的精度等级。其次，图7中采用训练外数据作为测试数据，无源电子器件设计参数选取case5：WP=2.6 mm，LP=1.7 mm，GP=1.3 mm。图7(a)为预测曲线，(b)为预测曲线与真实曲线的偏差，从图7中可以看出本文算法预测结果仍然与图6中结果相差不大，预测曲线围绕着真实曲线周围，而对比算法都出现了比较大的偏移，说明在非训练数据作为测试数据情况下，本文算法比对比算法具有更加明显的优势。最后，图8给出训练频率及其之外的预测曲线对比，无源电子器件设计参数选取case3：WP=2.3 mm，LP=1.2 mm，GP=0.9 mm。可以看出超出训练集的频率预测数据随着频率值的逐渐增大，3种算法都呈现逐渐远离真实数据的状态，但是本文算法相对最贴近真实数据。上述3个实验设计比较全面地阐述了本文所提算法的有效性。

5 结束语

    本文从提高无源电子元件模型准确度角度，设计了一种结合泛函链接模糊神经网络（FLFNN）和高斯改进和声搜索算法的无源电子器件信号检测模型。并通过实验仿真，对高斯改进和声搜索算法的参数选取进行实验分析，以及对FLFNN信号检测模型进行实验对比。仿真结果显示高斯改进和声搜索FLFNN无源电子元件信号检测算法具有更高的预测精度。

参考文献

[1] MALYSHEV I N，NIKULIN S M，UTKIN V N.Measuring the wave spreading parameters for elements of integrated microwave structures in strip lines[J].Metrologiya，2008，35(2)：32-42.

[2] CHENG Y H，CHEN K，BAI L B.Back propagation neural network based control for the heating system of a polysilicon reduction furnace[J].Review of Scientific Instruments，2013，84(12)：125108-125108.

[3] SOTIROUDIS S P，GOUDOS S K.Application of a composite differential evolution algorithm in optimal neural network design for propagation path-loss prediction in mobile communication systems[J].IEEE Antennas and Wireless Propagation Letters，2013(12)：364-367.

[4] 李松，刘力军，解永乐.遗传算法优化BP神经网络的短时交通流混沌预测[J].控制与决策，2011，26(10)：1581-1595.

[5] HYUNSEOK K，SEONGJU C S J.High-resolution touch floor system using particle swarm optimization neural network[J].IEEE Sensors Journal，2013，13(6)：2084-5295.

[6] DELINCHANT B，DURET D，ESTRABAUT L.An optimizer using software component paradigm for the optimization of engineering systems[J].The International Journal for Computation and Mathematics in Electrical and Electronic Engineering(COMPEL)，2007，26(2)：368-379.

[7] AKKALA A，BHATT D，DEVABHAKTUNI V.Knowledge based neural network appoaches for modeling and estimating radon concentrations[J].Environmental Progress & Sustainable Energy，2013，32(2)：355-364.

[8] 高学星，孙华刚，侯保林.使用不同置信级训练样本的神经网络学习方法[J].电子与信息学报，2014，36(6)：1307-1310.

[9] 欧阳海滨，高立群，邹德旋.和声搜索算法探索能力研究及其修正[J].控制理论与应用，2014，31(1)：57-61.

[10] YADAV P，KUMAR R，PANDA S K.Optimal thrust allocation for semisubmersible oil rig platforms using improved harmony search algorithm[J].IEEE Journal of Oceanic Engineering，2014，39(3)：526-539.

[11] HOANG D C，YADAV P，KUMAR R.Real-time implementation of a harmony search algorithm-based clustering protocol for energy-efficient wireless sensor networks[J].IEEE Transactions on Industrial Informatics，2013，10(1)：774-783.

[12] SAHIN S，TOLUN M R，HASSANPOUR R.Hybrid expert systems：a survey of current approaches and applications[J].Expert Systems with Applications，2012，39(4)：4609-4617.

[13] DURET D，GERBAUD L，WURTZ F.Modeling of passive electronic circuits with sensitivity analysis dedicated to the sizing by optimization[J].Modeling of Passive Electronic Circuits with Sensitivity，2007，4694：422-430.

[14] GAJZLER M.The idea of knowledge supplementation and explanation using neural networks to support decisions in construction engineering[J].Procedia Engineering，2013，57：302-309.

[15] SHANG F，HIROSE A.Quaternion neural-network-based PolSAR land classification in poincare-sphere-parameter space[J].IEEE Transactions on Geoscience and Remote Sensing，2013，52(9)：5693-5703.

[16] YANG C，LI Z，CUI R.Neural network-based motion control of an underactuated wheeled inverted pendulum model[J].IEEE Transactions on Neural Networks and Learning Systems，2014，25(11)：2004-2016.

[17] WANG Y，LI D，LU X.Self-organizing map neural network-based nearest neighbor position estimation scheme for continuous crystal PET detectors[J].IEEE Transactions on Nuclear Science，2014，61(5)：2446-2455.