0 引言

    与集中式电源系统相比，分布式电源系统具有可靠性高、便于模块化、标准化、集成化、易扩展、易维护等许多优点^[1]。因此，分布式电源系统在航天器电源、航空电源、电力系统、船舶、新能源汽车、计算机电源等领域得到了长足发展和广泛应用。然而，分布式电源系统结构多样，是非常复杂的非线性系统，尚未形成完善的设计和分析方法。本文介绍了分布式电源系统建模方法，对分布式电源系统中可能存在的非线性影响因素进行了归纳总结，为下一步研究奠定了基础。

1 分布式电源系统中的几种连接方式

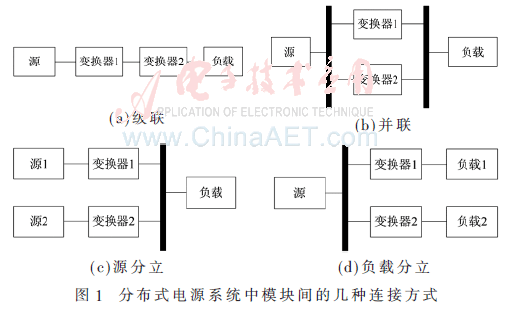
    分布式电源系统的拓扑结构可以看成“源+变换器+负载”。各模块间可以有以下几种连接方式^[2]：（1）级联；（2）并联；（3）源分立；（4）负载分立（如图1所示）。另外，分布式电源系统各模块间还有串联连接方式，由于这种连接方式并不常见，本文未予列出。由图1所示的连接方式可以组成更为复杂的分布式电源系统。这些不同的连接方式，使得分布式电源系统的设计和分析都比较复杂，同时也容易引起系统不稳定的问题^[3]。

2 分布式电源系统的建模方法

    对一个开关变换器而言，可以采用器件级模型尽可能准确地分析开关变换器的详细特性。但对于整个分布式电源系统而言，使用器件级模型来分析整个系统的特性是十分困难的。根据不同的需求，人们经常会从平均、功率守恒等观点出发采用简化模型来对分布式电源系统进行研究。在分布式电源系统的仿真分析中，大信号平均模型是一种相对合适的模型，它保留了系统的非线性特性，仿真时间较短。为了进一步降低分布式电源系统分析的难度，人们也提出了更为简化的模型：在分析两个级联的开关变换器时，后级变换器经常等效为一个简单的恒功率负载^[4]或恒阻负载和恒功率负载的组合^[5]。在静态模型的基础上，文献[6]则进一步建立了恒功率负载的高阶动态模型。

    在分布式电源系统中，经常把负载和变换器等效成为一个新的“负载”，负载是有源和无源功率器件的组合，这使得分布式电源系统的负载多种多样。概括起来，分布式电源系统的负载有以下几种基本类型：(1)恒功率负载：如变换器+电阻；(2)恒电阻负载：如常用的电阻；(3)恒流负载：如通过变换器给电池恒流充电；(4)恒压负载：如通过变换器给电池恒压充电。上述基本类型的负载可以组合为更为复杂的负载，这种组合可以是空间上的组合，如几种不同类型负载的并联；也可以是时间上的组合，如在一个时间段内是这种类型的负载，在下一个时间段内，则变为另一种类型的负载。

3 分布式电源系统中的非线性因素分析

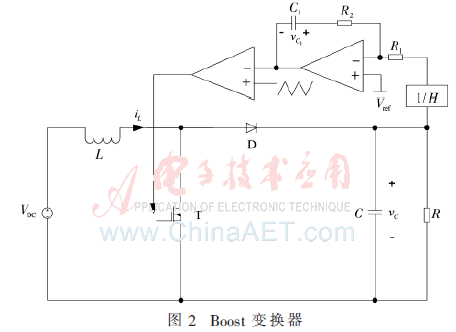
    在分布式电源系统中，开关变换器是造成系统非线性的最主要因素，其次是分布式电源系统中有些源和负载本身是非线性的。开关变换器是非常复杂的非线性时变离散系统。开关器件周期性的导通与关断使得开关变换器的主拓扑是一个时变电路。开关变换器又是一个离散系统，系统中既存在模拟量，又存在数字量。控制电路中的脉宽调制器将连续的模拟量转换为离散的开关序列（数字量），用以驱动开关器件的导通和关断。同时，开关变换器是复杂的非线性系统，下面结合图2所示的Boost电路对此进行分析。

3.1 占空比恒定时主拓扑电路结构切换造成的非线性

    主拓扑中开关器件的导通与关断会引起电路结构的改变。多个开关器件导通与关断的不同组合形成不同的电路结构。开关变换器中的开关器件主要有3种类型，第一种是以MOSFET、IGBT为代表的全控型器件，第二种是以二极管为代表的不控型器件，另外还有以晶闸管为代表的半控型器件。我们重点考虑在DC-DC变换器中使用的前两种类型的开关器件。全控型器件的通断由主拓扑外部的控制电路来进行驱动，不控型器件的通断则由主拓扑电路自身的结构和状态来决定。当图2所示的Boost变换器工作在CCM模式时，不控型器件二极管的开关状态与全控型器件的MOSFET形成互补，主拓扑有两种可能的电路结构；Boost变换器工作在DCM模式时，当MOSFET关断后，若电感电流不为0，二极管导通，若电感电流为0，二极管断开，所以DCM下Boost电路有3种可能的电路结构。

    占空比恒定时，变换器工作在稳态或者开环模式。在一个开关周期内，不同的电路结构所占时间的比例是不变的。主拓扑中的每一种电路结构，单独来看都是线性的，但不同的电路结构，电源是否接入电路、电容的充放电状态、电感电流的增减状态都不太一样，随着开关器件的导通与关断，开关变换器也在不同的电路结构间切换，从而造成了主拓扑电路的非线性，电流、电压等在电路结构切换时，发生非线性变化，形成开关纹波。

3.2 变化占空比造成的非线性

    若忽略掉开关纹波的影响，既然每一种电路结构都是线性的，那么主拓扑电路是否就是线性的了呢？要回答这个问题，我们先来建立变换器的大信号状态平均模型。

    由于开关纹波幅值很小，一般远小于平均值，可以近似认为状态变量的平均值与瞬时值相等，而不会引起较大的误差。对于CCM模式下的变换器，有两种可能的电路结构。设源为直流电压源，负载为阻值不变的电阻负载，开关周期为T_s，占空比为d。在每个开关周期的[0，dT_s]时间段内，主拓扑为一种电路结构，设状态方程为：

式中：A₁，B₁，C₁，D₁为系数矩阵；u为系统输入；y为系统输出；x为系统的状态变量。

    在每个开关周期的[dT_s，T_s]时间段内，主拓扑为另一种电路结构，设状态方程为：

式中：A₂，B₂，C₂，D₂为系数矩阵。

    根据状态平均的原理，最终的状态平均方程为：

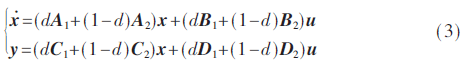
    若变换器工作在开环状态，占空比d可看成一个像电感、电容一样的固定不变的参数，则由式(3)可以看出，状态平均方程是线性的。但在闭环情况下，变换器的占空比是变化的，通常是电感电流和电容电压的函数，设d=f(x)，在状态方程中，会出现d·x=f(x)·x或d·u=f(x)·u，即会出现两个状态变量相乘或者状态变量与输入相乘的非线性乘积项。类似地，可建立DCM下Boost电路的状态方程模型，DCM下Boost电路的状态方程要复杂些，因为电感电流存在断续的状态。但同样地，状态方程中也会出现两个状态变量相乘或者状态变量与输入相乘的非线性乘积项。由此可见，使用状态平均方法消除了状态变量中由开关动作引起的纹波和由此带来的非线性，把时变系统转变为时不变系统，但状态方程中仍然含有非线性因素。这种非线性在状态方程中体现为状态变量相乘或状态变量与输入相乘的非线性乘积项；在由受控源替代开关元件的等效电路中体现为受控源的表达式为非线性乘积项；在物理意义上体现为在一个开关周期内，不同的电路结构所占时间的比例不是恒定不变或线性的，而是受状态变量控制的非线性表达式。在使用状态平均法建立小信号模型时，正是忽略了这些非线性乘积项，才使得小信号模型成为线性模型。

3.3 控制电路中的非线性

    控制电路中的非线性主要是由饱和现象造成的，包含以下两个方面：一是控制器的输出电压被供电电压所钳制，在电压模式的PWM控制器和电流模式的PWM控制器中会存在这样的饱和现象；二是占空比被限制在0到1之间，这样的占空比限制存在于任何一个开关变换中，实际工程中占空比的最小值和最大值可能不是0和1，而是介于0到1之间的值。

3.4 源和负载的非线性

    在分布式电源系统中，开关变换器的源和负载的非线性体现在以下两个方面。一方面是变换器的源和负载本身带有非线性。如源是蓄电池组、太阳电池阵等，其U-I特性曲线都呈现非线性特征。又如负载可能是电机、时断时续的加热器或者功率在某个范围内变化的变功率负载^[7]等非线性负载。另一方面是变换器引起的非线性。在分布式电源系统中，存在级联、并联、串联等情况，很多时候变换器不是直接和源、负载相连接，中间可能经过多个变换器，变换器的“源”和“负载”可能是其他变换器和源、其他变换器和负载的组合，这种组合常常呈现非线性特性。如两个开关变换器级联时，后级变换器和电阻负载作为前级变换器的“负载”，其负载特性可以看作恒功率负载，电阻负载是线性的，恒功率负载却是非线性的，而且，恒功率负载是对该负载特性的一种近似表示，真实的后级变换器和电阻负载的非线性特性要复杂得多。

3.5 器件的非线性

    电感、电容在通过不同的电流、电压时，其电感值、电容值可能发生变化，比较典型的是电感会有饱和现象。另外，器件的特性也会受温度和老化的影响而发生变化。器件的这些特性变化中含有非线性因素。

4 结论

    分布式电源系统中包含开关变换器等非线性模块，模块间存在级联、并联、源分立、负载分立等多种连接方式，使用线性理论的方法很难准确分析分布式电源系统的特性，这使得分布式电源系统的设计和分析都比较复杂，同时也容易引起系统的不稳定问题。本文介绍了分布式电源系统的建模方法，并对分布式电源系统可能存在的非线性影响因素做了全面分析，总结了5种造成分布式电源系统非线性的因素，为进一步使用非线性方法分析分布式电源系统的特性奠定了基础。

参考文献

[1] SURANYI G G.The Value of Distributed Power[C].IEEE Proceedings of Applied Power Electronics Conference and Exposition，1995：104-110.

[2] LUO S.A review of distributed power systems part I-DC distributed power system[J].Aerospace and Electronic Systems Magazine，2005，20(8)：5-16.

[3] 李安寿，张东来，杨炀.开关变换器的稳定性定义及分析方法[J].电力电子技术，2013，47(11)：27-29.

[4] LIUTANAKUL P，AWAN A，PIERFEDERICI S，et al.Linear stabilization of a DC bus supplying a constant power load[J].IEEE Transaction on Power Electronics，2010，25(2)：475-488.

[5] Zhang Fanghua，Yan Yangguang.Start-up process and step response of a DC-DC converter loaded by constant power loads[J].IEEE Transactions on Industrial Electronics，2011，58(1)：298-304.

[6] KNYAZKIN V，CANIZARES C A，S?魻DER L H.On the parameter estimation and modeling of aggregate power system loads[J].IEEE Transactions on Power Systems，2004，19(2)：1023-1031.

[7] 刘青.快速参考跟踪电源的研究[D].哈尔滨：哈尔滨工业大学，2013.