尹虹毅

　　（同济大学 电子与信息工程学院，上海 201804）

摘要：精神分裂症是最常见的精神疾病之一，目前具体病因尚未明确，准确诊断患病与否是治疗该疾病的前提。深度学习是一种构造多层神经网络的机器学习方法，具有发现数据中隐藏的分布式特征表示的能力。针对精神分裂症患者的脑电信号，提出了一种栈式自编码网络深度模型，以达到根据脑电信号自动识别受试者是否患病的效果。

关键词：深度学习; 精神分裂症；脑电

0引言

　　精神分裂症是一种持续、慢性的精神疾病，临床上表现为思维、情感、行为等多方面精神障碍，是精神病里最常见、最严重的一种［1］。精神分裂症病程多迁延并呈进行性发展，如果能够在患病早期准确诊断，并给予合理治疗，多数患者的病情是可以得到控制的。目前，科学家们尚未找出精神分裂症的具体成因，但研究显示，精神分裂症患者的大脑总体来说与非患者的大脑有区别［2］。

　　脑电（Electroencephalogram, EEG）是由脑部神经活动产生并且始终存在于中枢系统的自发性、节律性的电位活动。脑电是大脑的活动状态的反映，是帮助诊断大脑疾病的一种辅助检查方法。人类脑电波由5个主要波段构成：delta波(1~3 Hz)、theta波(4~7 Hz)、alpha波(8~13 Hz)、beta波(14~30 Hz)和gamma波(31~50 Hz)［3］。这5个波段的特征对于精神分裂症的诊断有着重要的参考价值。

　　本文提出了一种基于深度学习的精神分裂症患者的脑电分析方法：利用精神分裂症患者和正常对照者的脑电信号，训练深度神经网络，使该模型具有根据输入脑电信号，自动判别受试者是否患有精神分裂症的功能。

1深度学习网络

　　“机器学习”的概念自20世纪50年代提出以来就备受科技界的关注，而近年来“深度学习”逐渐成为机器学习研究中的一个新的领域［4］，并在计算机视觉和语音识别方面取得相关成果。

　　1.1多层特征学习

　　深度学习网络源于人工神经网络。目前，大部分机器学习算法都属于浅层学习，其局限性表现为对复杂分类问题图1深度学习网络的多层架构

　　的泛化能力受到制约。深度学习网络提供了一种多层特征学习的策略，即通过学习一种多层非线性网络结构，实现复杂函数逼近，表征输入数据从低层到高层的不同表示［5］，其多层架构示意图如图1所示。

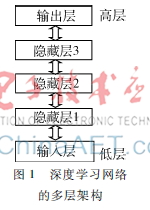
　　这种基于多层特征学习的深度结构由一个输入层、多个隐藏层和一个输出层构成。该模型的训练分为两个阶段：逐层贪婪训练阶段和微调阶段。在逐层贪婪训练阶段，每次只训练网络中的一层，即首先训练一个只含一个隐藏层的网络，仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网络，以此类推，直到训练完所有网络。在每一步中，把已经训练好的前层k-1固定，即把已经训练好的k-1层的输出作为第k层的输入。在微调阶段，这些层单独训练所得到的权重被用来初始化最终的深度网络的权重，然后使用梯度下降算法对网络中所有的权重值进行优化。

　　深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据中隐藏的分布式特征表示［6］，这对于复杂模型的分析具有相当重要的作用。当数据充足时，该算法可以学习到丰富的信息，故训练的数据越多，其效果越好。因此，深度学习适用于数据信息量较大的分析场合。

　　1.2栈式自编码网络

　　1.2.1自编码网络

　　自编码神经网络是一种无监督学习算法，它通过设置目标值等于输入值，来学习输入数据的编码方式。图2是一个自编码神经网络的示例。

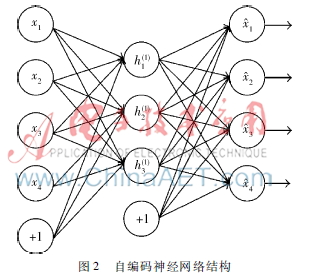
　　假设有一个固定无标签样本x(1),…,xm,它包含m个样例。对于单个样例  x，定义其代价函数为：

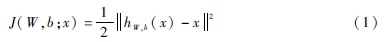
　　其中，W为网络的权重，b为网络的偏差,hW,b(x)为网络的输出。

　　对于全部样本，定义整体代价函数为：

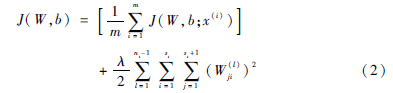
　　其中，λ为权重衰减参数。第一项为每个样例的代价函数的平均；第二项为权重衰减项，其目的是减小权重的幅度，防止过度拟合。

　　自编码神经网络的目标是尝试逼近一个恒等函数，从而使得输出hW,b(x)接近于输入x。通过在自编码神经网络加入某些限制，可以从输入数据中提取出一些有用的结构。例如，输入x是一个100维的数据，即m=100,若隐藏层有50个神经元，即L2=50，输出也是100维的,hW,b(x)∈R100。由于隐藏层只有50个神经元，自编码神经网络被迫去学习输入数据的压缩表示。如果输入数据中隐含着一些特定的结构，比如某些输入特征是彼此相关的，那么通过这一算法就可以发现输入数据中的这些相关性。即使在隐藏层神经元的数量较大的情况下，甚至多于输入层神经元的数目，仍可通过给自编码神经网络施加一些其他的限制条件，例如稀疏性限制［7］，来发现输入数据的结构。

　　1.2.2稀疏性

　　假设神经元的激活函数是sigmoid函数，当神经元的输出接近于1时认为它被激活，而输出接近于0时认为它被抑制，那么使得神经元大部分的时间都处于被抑制状态的限制称为稀疏性限制［8］。

　　若在给定输入为x情况下，自编码神经网络隐藏神经元j的激活度为a(2)j，则该隐藏神经元j在训练集上的平均活跃度为：

　　根据稀疏性的定义，限制隐藏神经元j的平均活跃度接近于0，即:

　　其中，ρ是稀疏性参数，通常取一个接近于0的较小的值。

　　同时，在代价函数中加入一个额外的惩罚因子，惩罚那些ρ∧j和ρ有显著不同的情况，从而使得隐藏神经元的平均活跃度保持在较小范围内。本算法选择相对熵（KL divergence），即惩罚因子:

　　∑s2j=1KL(ρρ∧j)（5）

　　其中，KL(ρρ∧j)=ρlogρρ∧j+(1－ρ)log1－ρ1－ρ∧j是一个以ρ为均值和一个以ρ∧j为均值的两个伯努利随机变量之间的相对熵。

　　在加入了稀疏性限制后，总体代价函数可以表示为:

　　Jsparse(W,b)=J(W,b)+β∑s2j=1KL(ρρ∧j)（6）

　　其中，J(W,b)如之前所定义，而β为控制稀疏性惩罚因子的权重。

　　1.2.3栈式自编码算法

　　栈式自编码网络是由多层稀疏自编码网络组成的神经网络，其前一层自编码网络的输出作为其后一层自编码网络的输入［9］。栈式自动编码网络的结构示意图如图3所示。

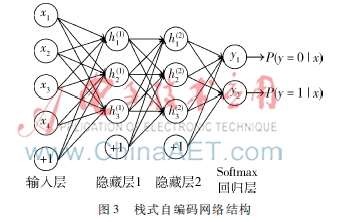
　　栈式自编码网络的训练方法如下：在训练每一层参数时，固定其他各层参数保持不变。在上述预训练过程完成之后，进行微调，即通过反向传播算法同时调整所有层的参数以改善结果。

　　1.3Softmax回归

　　Softmax回归解决的是多类分类问题，其思想如下：对于给定的测试输入样例（x,y），利用假设函数计算属于每一个类别j的概率值p(y=j|x)，则该假设函数hθ(x)形式如下：

2基于栈式自编码的精神分裂症脑电分析

　　2.1数据集

　　本文所用数据均为医院采集的真实数据，其中有62个精神分裂症患者，88个健康对照者。被试者的EEG信号均在静息闭眼的状态下采集。EEG的信号使用含有 64 个导联的放大器进行数据的采集，采样频率为1 000 Hz，所采集的样本数据都包含64个导联上2~3 min的时域数据。

　　2.2脑电特征提取

　　因为精神分裂症是由于大脑异常引起的，在得到的64个导联的信号中，选取了59个最能直接反映大脑活动状态的导联，分别是AF3、AF4、AF7、AF8、C1、C2、C3、C4、C5、C6、CP1、CP2、CP3、CP4、CP5、CP6、CPz、Cz、F1、F2、F3、F4、F5、F6、F7、F8、FC1、FC2、FC3、FC4、FC5、FC6、Fp1、Fp2、Fpz、FT7、FT8、Fz、O1、O2、Oz、P1、P2、P3、P4、P5、P6、P7、P8、PO3、PO4、PO7、PO8、POz、Pz、T7、T8、TP7、TP8。

　　由于深度学习网络需要大量训练样本，在此，对每个人的时域数据进行截取多个时间片段样本的处理，将每个时域数据截成长度为2 s、重叠为25%的多个片段样本。通过这样处理后，获得8 709个精神分裂症患者的时间片段，11 542个健康对照者的时间片段样本。

　　对每个样本，采用快速傅里叶变换获取其功率谱密度。接着，提取其在频域中5个频带的能量作为特征，即delta波段(1~3 Hz)、theta波段(4~7 Hz)、alpha波段(8~13 Hz)、beta波段(14~30 Hz)和gamma波段 (31~50 Hz)的能量。最后，每个样本提取到295个特征，作为栈式自编码网络的输入。

　　2.3栈式自编码网络的实现

　　本文提出的用于精神分裂症脑电分析的栈式自编码网络由多个自编码网络和一个Softmax回归层构成。在完成训练后，这个栈式自编码网络能够根据测试脑电信号实现自动判别该脑电所属实验者是否患有精神分裂症。

　　这个栈式自编码网络首先对网络中的每层到进行逐层贪婪训练：输入的数据（295个频域能量特征）被用于训练第一个稀疏自编码网络，以获取输入数据的初级特征h(1)。在此，使用梯度下降方法来最优化代价函数，从而学习出第一个网络的最佳权重参数。

　　在最佳权重学习完毕后，使用输入数据在第一个网络进行前向传播，得到输入数据的初级特征h(1)。而第一个网络得到的特征h(1)被用作第二个网络的输入，采用同样的方法获取第二个网络的特征h(2)。将前一层网络学习到的特征作为下一层网络的输入，循环以上步骤，可获得每层网络的最佳权重参数。最后一层隐藏层的特征h(n-1)被用作Softmax回归层的输入，以获取其最佳权重参数。

　　在完成了逐层最佳权重参数学习后，对整个网络进行微调，以获得最佳全局权重。

3实验分析

　　本实验将从两个方面进行分析。为探究隐藏层节点数对识别效果的影响，先探究只含有一个隐藏层的自编码网络的隐藏层节点数对识别效果的影响，之后再探究栈式自编码网络的隐藏层层数对识别效果的影响。

　　3.1单层网络隐藏层节点数对实验结果的影响

　　首先构造了一个输入层含有295个节点、输出层为2个节点Softmax回归层的单隐藏层自编码网络，令其隐藏层节点数为10~1 000，以观察隐藏层节点数对精神分裂症脑电的识别率，实验结果如图4所示。

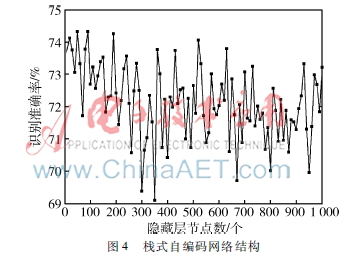
　　从图4可以看到，采用了稀疏自编码网络对精神分裂症脑电具有较好的识别效果，不同隐藏层节点所获得的识别准确率均在72%左右，其中当隐藏层节点数为80、110、200时，识别率最高，超过了74%。

　　3.2网络层数对实验结果影响

　　为探究栈式自编码网络的隐藏层层数对识别效果的影响，分别构造了隐藏层层数为2层、3层和4层的栈式自编码网络，具体网络参数和实验结果如表1所示。

　　从表1结果可以看到，当隐藏层数目增加时，该栈式自编码网络对精神分裂症脑电的识别率有小幅度的提升。

4结论

　　针对精神分裂症难以诊断的问题，本文提出了利用深度神经网络对精神分裂症脑电进行分析判别的方法。该方法通过建立含有多个隐层结构的栈式自编码网络，从大量脑电数据中获取隐含结构信息，以提高分类识别以及预测的准确性。实验验证了所提出的方法的有效性，对 62个精神分裂症患者和88个健康对照者的脑电数据的识别准确率较高，且有较好的适应性。从实验分析可得，实验结果与理论分析基本相符。

　　在未来的研究中，要解决的主要问题有:（1）深度神经网络层数的极限在哪里，是否存在某个固定的层数使得该网络达到性能最优；（2）如何决定某类问题深度学习的层数和隐藏层节点的个数。

参考文献

　　［1］ 管丽丽,杜立哲,马弘. 精神分裂症的疾病负担(综述)［J］. 中国心理卫生杂志,2012,26(12):913919.

　　［2］ 宋安林. 精神分裂症脑组织各部位神经病理改变对比研究［D］.重庆：重庆医科大学,2010.

　　［3］ TEPLAN M. Fundamentals of EEG measurement ［J］. Measurement Science Review, 2002, 2(2): 110.

　　［4］ YOSHUA B, COURVILLE A, VINCENT P. Representation learning: a review and new perspectives［J］.IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013,35(8):17981828.

　　［5］ SCHLKOPF B, PLATT J,HOFMANN T. Greedy layerwise training of deep networks［J］. Advances in Neural Information Processing Systems，2007，19：153160.

　　［6］ HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks［J］. Science， 2006，313（5786）:504507.

　　［7］ OLSHAUSEN B A, FIELD D J. Sparse coding with an overcomplete basis set: a strategy employed by VI?［J］. Vision Research，1997，37（23）: 33113326.

　　［8］ LEE H， BATTLE A， RAINA R， et al. Efficient sparse coding algorithms［C］.  Conference on Neural Information Processing Systems, 2007:801808.

　　［9］ YOSHUA B, DELALLEAU O. On the expressive power of deep architectures［C］. Interrational Couference on Discovery Science,2011,6925:1836.