邓方华1，许有才1，陶然1,2，郭澍2，李新仕2，苟敏1，李琨1

　　（1.昆明理工大学 信息工程与自动化学院，云南 昆明 650500；2.云南省特种设备安全检测研究院，云南 昆明 650228）

      摘要：针对自动扶梯故障问题，以层次分析和差分进化算法极限学习机相结合的方式快速、准确地分析了自动扶梯发生的故障问题。首先，用层次分析法计算出各故障因数的权值，选取权值较大的一部分因素作为输入。然后，建立DEELM安全评测模型并与ELM模型比较，得出自动扶梯安全程度等级并说明自动扶梯的安全性。研究表明：对于很难或无法获得故障因素准确值的自动扶梯而言，层次分析法是一种有效实用的可靠性分析方法，再结合差分进化算法极限学习机的全局寻优能力，对自动扶梯故障问题的检测更加快速、准确。

　　关键词：自动扶梯；层次分析法；差分进化算法极限学习机；自动扶梯故障

0引言

　　云南省质量技术监督局科技计划项目资助（2013ynzjkj02）自动扶梯是一种带有循环运行梯级的典型机电合一设备，主要用于向上和向下倾斜运输乘客，已经成为当前轨道交通中重要的代步工具之一，其重要性毋庸置疑。这就要求自动扶梯具有很好的可靠性和安全性［1］。因此，需要依靠先进的故障诊断方法对设备中存在的危险因素进行识别和分析，判断设备发生事故和危害的可能性及其严重程度，提高自动扶梯的运行效率［2］。

　　为了对影响自动扶梯故障的因素进行科学准确的划分，同时结合专家意见进行安全分析，对各评价指标权重系数进行确定,应用差分进化算法极限学习机对自动扶梯的故障问题进行分析，合理有效地解决了差分进化算法反应速度慢和不稳定的缺点。

1层次分析方法

　　自动扶梯系统是一个多层次、非线性、动态、模糊的复杂系统，要科学、合理地评价自动扶梯系统的安全性，首先必须确定能够反映自动扶梯系统安全状况的因素［3］。层次分析法（Analytic Hierarchy Process，AHP）在对复杂系统的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使复杂系统的影响因素数学化、层次化。层次分析法的步骤可归纳如下。

　　1.1建立层次结构模型

　　在分析自动扶梯检测问题时，首先要简化分解问题，从而构造出一个层次分明的结构模型，如图1所示。该模型分为三层：目的层，准则层，方案层。

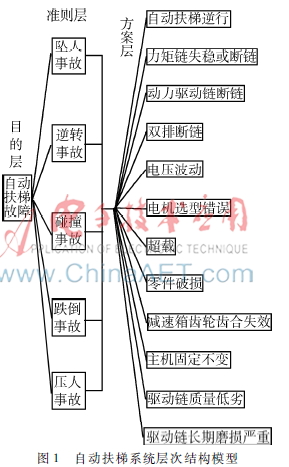
　　影响故障的因素有很多，其中每个因素所占的比例也不一样，在实际应用中，应当根据各因素的重要程度对其赋予相应的权重［4］。然而在具体操作的过程当中有些因素难以定量分析，只能定性分析。因此，本文根据专家意见对层次结构模型中的准则层进行分析，并引用数字1~9及其倒数作为标度来定义判断矩阵（见表1）［5］。从属上一层次A的每个因素构成判断矩阵。

　　a51a52a53a54a55 表1判断矩阵标度定义标度含义1两个因素相比，同样重要3两个因素相比，前者稍微重要5两个因素相比，后者明显重要7两个因素相比，前者强烈重要9两个因素相比，前者极端重要2，4,6,8表示上述相邻判断值的中间值倒数若因素i与因素j的重要性之比为aij,那么因素j与因素i的重要性之比为aji=1/aij

　　1.3一致性检验

　　（1）计算一致性指标CI

　　CI=λmax－nn－1（1）

　　其中，λmax为判断矩阵的最大特征值。

　　（2）随机一致性指标RI（见表2）［6］。

     （3）计算一致性比例CR

　　如CR<0.10，则认为判断矩阵的一致性是合理可接受的，否则需要对判断矩阵进行一定的修改。

2差分进化算法极限学习机

　　2.1极限学习机

　　极限学习机(Extreme Learning Machine，ELM）是由黄广斌提出来的求解神经网络算法［7］。ELM最大的特点是对于传统的神经网络，尤其是单隐层前馈神经网络(SLFNS)，其学习算法速度更快［8］。对于一个单隐层神经网络，假设有N个任意的样本(xi,ti)，其中

　　Xi=［xi1,xi2,...,xin］T∈Rn,ti=［ti1,ti2,...,tim］T∈Rm。

　　对于一个有个隐层节点的单隐层神经网络可以表示为［9］:

　　∑i=1βig(Wi*Xj+bi)=Oj,j=1,...,N

　　其中，g(x)为激活函数，Wi=［wi,1,wi,2,...,wi,n］T为输入权重，βi为输出权重，bi是第i个隐层单元的偏置。

　　为了使得输出误差最小，可以表示为∑j=1oj－tj=0，即表示存在βi，Wi和bi，可以使得∑i=1βig(Wi*Xj+bi)=Tj,j=1,...,N,可表示为：

　　Hβ=T

　　其中H是隐层节点的输出，β为输出权重，T为期望输出。

　　为了能够达到训练单隐层神经网络的目的，需要获取i,i和i的值并且使得

　　H(i,i)－T=minw,b,βH(Wi,bi)β－T

　　其中i=1,…，这等价于最小化损失函数

　　E=∑Nj=1∑i=1βig(Wi·Xj+bi)－tj2

　　在ELM算法中, 当输入权重Wi、隐层的偏置bi被随机确定后，隐层的输出矩阵H也可以被确定［10］。因此可以把训练单隐层神经网络转化为求解一个线性系统Hβ=T。并且输出权重β可以由下式确定：

　　其中，H是矩阵H的MoorePenrose广义逆。综上所述，极限学习机的实现步骤为：

　　（1）根据训练样本集［xi,yi］（i=1,2,3,...N,N为训练样本个数），激励函数g(x)以及隐含层单元个数；

　　（2）随机生成输入权值矩阵Wi以及隐含层偏置矩阵bi；

　　（3）根据式（4）求出隐含层输出矩阵H；

　　（4）根据式（5）求出输出权重β。

　　2.2差分进化算法极限学习机

　　差分进化算法DE是一种新兴的进化计算技术。它是由Storn等人于1995年提出的，和其他演化算法一样，DE是一种模拟生物进化的随机模型，通过反复迭代，使得那些适应环境的个体被保存下来［11］。

　　差分进化算法极限学习机（DEELM）的实现步骤如下。

　　2.2.1初始化

　　首先初始化种群X0=［x01,x02,…x0NP］,NP为种群规模。设置极限学习机隐含层单元个数以及激励函数g(x)。个体X0i=［x0i,1,x0i,2,…,x0i,D］用于表征问题解，D为优化问题的维数［12］。

　　其任意一个种群个体tr,g由ELM 的输入权值矩Wi=［wi,1,wi,2,...,wi,n］T和隐含层偏置矩阵(bi) 组成，即

　　t=［w11,w12…w1n,…,wk1,wk2,…wkn,b1,…bk］

　　对于每一个种群个体t，按照式（4）计算出隐含层输出矩阵H，然后再按照式（5）得到输出权重β，最后计算每个个体的均方根误差（RootMeanSquare Error,RMSE）［13］。

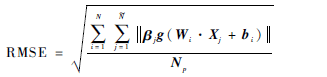
　　2.2.2变异

　　对于任意一个目标向量tr,g，取式（6）变异方式进行变异操作［14］。

　　Vr,g+1=tr1,g+F·(tr2,g－tr3,g)（6）

　　式中的r1,r2,r3表示种群个体序号，三者互不相同，且分别与目标序号r不同；tr1,g为父代基向量；(tr2,g－tr3,g)为父代差分向量；F为缩放比例因子。

　　2.2.3交叉

　　利用式（7）对tr,g和由式（6）生成的Vr,g+1实施交叉操作，生成实验个体Ur,g+1。

　　ur,g+1=vr,g+1,if(rand(j)≤CR) or (j)=rndr(i)

　　tr,g+1,Otherwise （7）

　　其中，j=［0,1,2,...,i］,rand(j)为［0,1］之间的均匀分布随机数［15］；CR为范围在［0,1］之间的交叉概率；rndr(i)为{1,2，...，D}之间的随机量。

　　2.2.4选择

　　利用式（8）对由式（7）生成的实验个体Ur,g+1和tr,g的目标函数进行比较，选择目标函数值低的个体作为新种群的个体Xr,g+1［16］，即

　　其中f为目标函数。

3自动扶梯故障检测实例

　　3.1层次分析法计算权重向量W

　　根据式（9）求得自动扶梯的故障因素的权重向量，计算步骤如下：

　　（1）判断矩阵A的元素按行相乘得一新向量［17］；

　　（2）将新向量的每个分量开n次方；

　　（3）将所得到向量归一化，便可得到权重向量Wi。

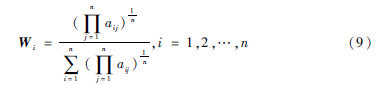
　　从图1可以得到对于自动扶梯故障的各种评价因素，根据式（9）计算各因素的权重，如表3所示［18］。

　　表3评价因素及其相关权重评价因素权重自动扶梯逆行*0.413 2力矩链失稳或断链*0.321 2动力驱动链断链*0.343 1 双排断链*0.524 3电压波动*0.212 1电机选型错误*0.121 2超载0.517 1零件破损*0.332 1减速箱齿轮齿合失效*0.423 1主机固定不变*0.366 4驱动链质量低劣*0.502 3驱动链长期磨损严重*0.393 5由表3可以得到影响自动扶梯故障因素的权重，从各个部分的权值来看，双排断链及超载对自动扶梯出现故障的影响比较大。但结合自动扶梯领域专家的经验，由超载导致自动扶梯出现故障并引起事故的几乎没有，而且对于超载问题有非常严格的评测系统和警戒方法，因此表3中11个标记“*”的权重值较大的评测因素可以作为 DEELM模型的输入。

　　3.2建立DE-ELM的评估模型

　　将安全程度分为4 个等级：很安全(Ⅰ级)，比较安全(Ⅱ级)，不安全(Ⅲ级)，很不安全(Ⅳ级)。因DEELM模型的输入输出均为数值，需将安全等级量化，以0.0~0.5代表很不安全，0.5~0.7 代表不安全，0.7~0.9 代表比较安全，0.9~1.00 代表很安全。以云南省特种设备安全检测研究院二十多年的分析研究数据为基础，选取20组由3.1节中层次分析法所确定的11个评价因素作为训练样本，对DEELM模型进行训练，训练过程将样本分为2组进行交叉验证。

　　3.3结果分析

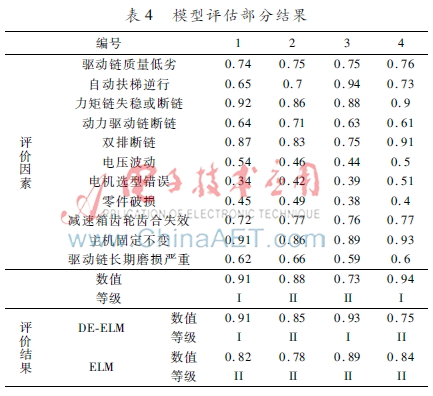
　　为验证DEELM模型的评估效果，将20组数据作为训练样本，构建成为标准ELM模型，可以作为对比。DEELM模型迭代次数取200，训练目标取为0.000 1，隐含层节点取20。ELM模型的评估结果有4次与实际不符，评估准确率仅为80%，DE-ELM 模型的评估结果仅有2 次与实际不符，评估准确率较标准ELM模型提高10%，高达90%，模型评估部分结果如表4所示。由表4可知，DE-ELM模型的安全评价是可靠的。

4结论

　　利用差分进化算法实现的全局寻优能力的极限学习机，克服了ELM收敛速度慢、易陷入局部最优的缺点。以层次分析法分析出权重比值较高的评价因素，以此为基础，建立DEELM安全评价模型，并对自动扶梯的安全性进行验证分析。结果表明DEELM模型所得出的结果与预期结果一致，而且对比结果显示DEELM模型下自动扶梯安全程度等级高于ELM模型。

　　参考文献

　　［1］ 宗群，马宏波，王中海.基于NNFPN模型的电梯故障诊断方法的研究［J］.控制与决策，2005,20(4)：241244.

　　［2］ ZHANG G M,CAIL,ZHU W,et al.Application of evaluation model based on fuzzy analytic hierarchy process in elevator election［J］.ElevatorWorld,2006,54(10):223229.

　　［3］ TANNK A H, FAN L T,LAI F S,et al.Faulttree analysis by fuzzy probability［J］.IEEE Transactions on Reliability,1983,32(5):427431.

　　［4］ 孙余凯，项绮明，徐绍贤，等.新型电梯故障检修技巧与实例［M］.北京：电子工业出版社，2008.

　　［5］ 王钦方,企业安全模型研究［J］. 中国安全科学学报,2005,15(12):3337.

　　［6］ ANSI/ASME A17.1b2003, 电梯和自动扶梯的安全性法规［S］.2003.

　　［7］ 王志强，杨春帆，姜雪松.最新电梯原理、使用与维护［M］.北京:机械工业出版社，2006.

　　［8］ 何德芳，李力，和济.失效分析与故障预防［M］.北京:冶金工业出版社，1990.

　　［9］ WILFRIED H, NICKOLAJ K. Famocutn & cutqn: programs for fast analysis of large fault trees with replicated & negated gate［J］.IEEE Transactions on Reliability,1995,44(3):367376.

　　［10］ 杨启文,蔡亮,薛云灿. 差分进化算法综述［J］.模式识别与人工智能，2008,21(4):302310.

　　［11］ 郭金玉,张忠彬,孙庆云. 层次分析法的研究与应用［J］. 中国安全科学学报,2008,18(5):148153.

　　［12］ 夏萍,汪凯,李宁秀,等.层次分析法中求权重的一种改进［J］. 中国卫生统计,2011,28(2):151154.

　　［13］ YU P, LEE J H. A hybrid approach using twolevel SOM and combined AHP rating and AHP/DEAAR method for selecting optimal promising emerging technology［J］. Expert Systems With Applications,2013,401(2):3142.

　　［14］ 周艳平,顾幸生.差分进化算法研究进展［J］.化工自动化及仪表，2001,31（6):100105.

　　［15］ 李维刚,贾树晋,郭朝晖.基于分解的多目标差分进化算法及其应用［J］.信息与控制，2009,43(3):141142.

　　［16］ 王艳宜.改进差分进化算法及其应用［J］. 机械设计与研究，2010,44(3):8792.

　　［17］ GB 168992011.自动扶梯和自动人行道的制造与安装安全规范［S］.2011.

　　［18］ 毛怀新.电梯与自动扶梯技术检验［M］.北京：学苑出版社，2001.